高壓線塔規劃的物理解法

龔文鑫

（清華大學附屬中學，北京 100084）

在我國基礎建設日益蓬勃的今天，配套建設高壓線塔等供電設施的需求也在不斷擴大。本文以高壓線塔的鋪設為例，討論如何在已知每一地點線塔造價（不同地理位置下的線塔架設難度不一）且路程足夠遠的情況下確定能使高壓線塔總造價最小的線塔建造軌跡。由于單純從各地線塔造價入手難以解決，文章通過借助費馬原理轉化，在線塔軌跡和幾何光學三大定律之間建立聯系，以便通過相對簡單的數學計算和幾何光學推論確定線塔架設軌跡。

1 模型建立

我們考慮的問題是在A 地和B 地建造一系列的高壓線塔，并且總造價最少。在問題的考慮過程中，每一個線塔的造價成本與建造地點有關，記作n（x，y），相鄰兩線塔之間的距離始終不變，記作L，線塔數目記作N，則總費用p 為：

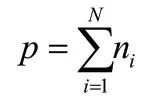
式中，ni為建造第i 個線塔所需成本。

由于相對實際路線長度，線塔之間的距離L 可以認為接近于0，所以在模型中，兩地之間線路軌跡可看作平滑曲線，求和可以轉化為積分。在轉化的過程中將，由于L 很小且為定值，利用建設線塔過程中每一點鋪設成本分布函數n（x，y）可以得知

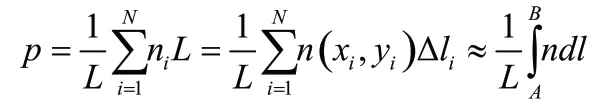
2 使用光學方法求解模型

2.1 模型轉化為光學問題

通過觀察總費用p 的表達式，可以看出∫ ndl 和費馬原理里面的光程表達式很類似。如果我們認為造價成本分布函數就是折射率，則光從點A 沿著實際的線塔設計路線射至點B，時長t 為

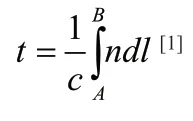
2.2 幾何光學解法

由于費馬原理和幾何光學三大基本定律是相互等價的[1]，也即有：

（1）光線在均勻介質中沿直線傳播。

（2）光的反射定律：光線在界面上的反射，入射角必須等于出射角。

（3）光的折射定律：n sin θ 為一個常數。

因此模型可以使用幾何光學的三大基本定律求解，將結論代入模型，為滿足總造價p 最小化，有如下推論：

（1）線塔在造價成本與建造地點無關的情況下應沿直線建造。

（2）在線塔規劃路線中某區域不可建造（即費用無限大時）需要沿反射路徑。

（3）在兩造價不同區域相交時線塔路徑滿足n sin θ 是一個常數，其中θ 表示的是折射角，在模型中的含義是路徑的切線方向和n（x，y）的等值面法線方向之間的夾角。

3 一個特殊情形

我們考慮在原點A（0，0）和終點B（xB，yB）之間的線塔造價分布函數n（x，y）以一次函數的形式遞增，也即可以表達為函數n=ax+b（a，b 為常數且n>0恒成立）。

由于n sin θ 為定值，通過與文獻[2]對比，可以得到實際光線軌跡方程：

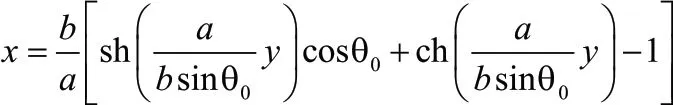
式中，θ0代表的是入射光線與x 軸正方向的夾角，也即入射光線的折射角。

由于軌跡經過B（xB，yB），所以需要滿足可解得θ0，將θ0的結果重新代入可得軌跡方程。

我們畫出a>0的軌跡方程的示意圖，如圖1。

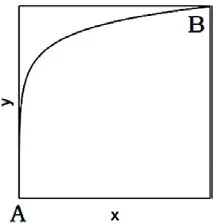
圖1

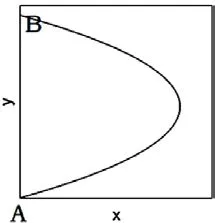
圖2

可以看出，軌跡的斜率越來越小，這也和預期是一致的，因為此時的折射率隨著x 的增加而增加，折射角θ 應該越來越小，而θ 角正是軌跡的切線方向和x 軸正方向的夾角。

我們畫出a<0的軌跡方程的示意圖，如圖2。假設B 點的橫坐標為0，則圖示中的曲線只是一條備選軌跡，還有一條真實的光線為直線x=0，具體的軌跡選哪一條，還需要對比兩條軌跡的工程造價，這是因為，在直線x=0的情形中，軌跡的長度較短，所造線塔的數目較少，而在圖2所示的情形中，軌跡的長度較長，所造線塔的數目較多，但是每個線塔的造價會低一些。

這種情況可以推廣到n 只和x 有關的情形，記作n（x），此時軌跡y（x）的導數為

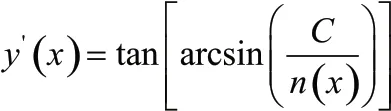
式中，C 是待定系數。

求出該函數的原函數為

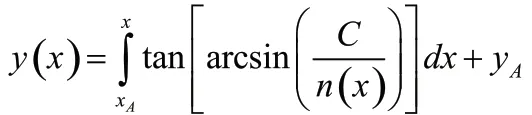
代入B 點坐標，使用y（xB）=yB能夠求出來待定系數C 的取值，即可得到軌跡。

4 一般情形的討論

一般情況下，我們設計的線塔路線規劃有如下結論：

（1）如果軌跡經過造價特別大的地方，一定要以直線的方式快速通過，這是因為在該處n 特別大，此時θ≈0°，這也就意味著，該處的軌跡切線方向和該處的折射率等值面的法線方向是一致的，也就意味著軌跡在該區域內部的長度盡量小。

（2）如果軌跡經過造價特別小的地方，那么此時光線的n sin θ 值一定比較小，而經過該處時，θ≈90°，這也就意味著該處的軌跡切線方向和折射率等值面基本上相切，也就意味著軌跡在該區域的長度盡量長。

一般情形下的求解方案還可以轉化為一個實驗物理過程，設空間中各點的折射率由造價分布函數已知，現在由A 點出射一條光線，隨著出射方向的改變，這條光線的軌跡也會發生改變，可以通過實驗來看到光線隨著出射方向的變化規律。在這些光線中，其中軌跡經過B 點的光線可能有若干條，因此可以作為備選的軌跡，在比較這些備選光線對應的造價p，取其中p 最小的光線即可得到問題的答案。

5 結束語

本文通過對路線規劃問題建模，結合費馬原理轉化為了一個可求解的光學問題。需要注意的是，求解方案中光線的軌跡實際上取得是極值，而不是最小值[1，3]，所以該方法有一定的局限性。需要在實際計算中與另一條直線光路進行對比。本文詳細介紹了線塔造價線性規律上升時的軌跡求解過程，同時提及了n 是一元函數時的推廣情況。在幾何光學基本定律的基礎上可以通過諸多數學手段或者物理實驗手段來尋找更廣泛，更普適的高壓線塔架設規律。希望日后能有更多拓展。