軸承-錐齒輪傳動轉子系統非線性動力學模型

王靜　王瑾　崔巍

摘 要：軸承-錐齒輪傳動轉子系統廣泛應用于動力、機械、車輛、航空航天等相關領域。本文考慮了軸承力、齒側間隙、靜態傳動誤差等非線性因素后建立了具有七自由度的軸承錐齒輪非線性動力學模型，希望能為相關領域的非線性動力學研究分析起到鋪墊作用。

關鍵詞：軸承;錐齒輪;非線性動力學

DOI：10.16640/j.cnki.37-1222/t.2019.23.015

0 引言

在一些空間布置受到限制或傳動需變向的場所經常會使用軸承-錐齒輪傳動轉子系統，而目前對軸承齒輪轉子的非線性動力學特性的研究中，一般將非線性軸承力和齒輪嚙合力相互獨立進行分析，沒有考慮兩者之間的耦合作用對其系統的影響，為此本文考慮了軸承力、齒側間隙、靜態傳動誤差等因素耦合作用下，建立軸承-錐齒輪傳動轉子系統非線性力學模型。

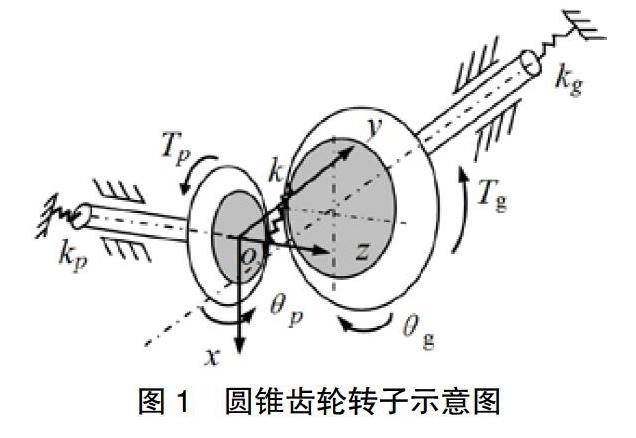
1 結構模型及假設

建立軸承-錐齒輪傳動轉子系統的非線性動力學模型是本文研究的目的，現作如下假設：（1）兩個轉子的徑向支承為軸承支承，軸向支承簡化成線性彈簧支承;（2）考慮了兩個齒輪嚙合時的齒側間隙，且齒輪嚙合剛度的時變部分按正弦變化;（3）（xi，yi，zi）為兩個齒輪的質心坐標，其扭轉角位移分別用θp和θg表示，系統的結構如圖1所示。

2 非線性動力學模型

根據牛頓定律，小齒輪和大齒輪的振動方程可表示為八自由度非線性微分方程：

式中各參數所代表的物理意義如下表所示。

因而方程組（1）前6式加式（3）即為圖（1）軸承-錐齒輪傳動轉子系統的具有七自由度的非線性動力學模型，后期可對該動力學模型進行數值或解析求解，分析其動力學特性。

3 結論

首先對軸承-錐齒輪傳動轉子系統作了相關假設，在考慮了軸承力、齒側間隙、靜態傳動誤差等非線性因素后，建立了具有七自由度的軸承-錐齒輪傳動轉子系統非線性動力學模型，期望能在相關科研中起到拋磚引玉的作用，后期可對其方程進行求解，深入研究其非線性動力學特性。

參考文獻：

[1]張耀強，陳建軍，唐六丁等.滾動軸承-Jeffcott轉子系統非線性動力響應分析[J].振動與沖擊，2008，27（05）：56-59.

[2]李明，阿梅.非線性油膜力作用下圓錐齒輪傳動系統的動力學行為[A].第十屆全國振動理論及應用學術會議論文集（2011）上冊[C].2011.

[3]王靜.滾動軸承支承錐齒輪傳動轉子系統非線性動力學研究[D].西安科技大學，2014.

西安科技大學高新學院校內基金項目：軸承轉子非線性動力學（編號2017KJ-05）

作者簡介：王靜（1988-），女，陜西西安人，研究生，教師，講師，研究方向：工程力學，從事教學工作。