汽車差速器錐齒輪差速工況下的潤滑特性研究*

(青島理工大學機械與汽車工程學院 山東青島 266520)

汽車差速器是汽車重要的組成部分，在汽車的轉向系統中發揮著重要的作用，能夠保證汽車轉向時內外輪速度差，避免輪胎在地面上的滑移和滑轉[1]。現在汽車差速器多數是由錐齒輪副組成，通常是由2個行星直齒錐齒輪和2個半軸直齒錐齒輪組成。當汽車兩側車輪轉速相同時，行星齒輪繞半軸軸線轉動，稱為公轉；當兩側車輪阻力不同時，行星齒輪在公轉的同時繞自身軸線轉動，稱為自轉。行星齒輪自轉時，2個半軸齒輪轉速不同，此時整個差速器處于差速工況。當汽車直線行駛工況向差速工況過渡時，行星齒輪和半軸齒輪往往需要承受較大的載荷，傳動過程中會出現大的滑動速度，如若齒面潤滑不當，行星齒輪和半軸齒輪的接觸表面會發生摩擦和磨損，嚴重時出現齒面膠合現象，導致齒面失效，特別對于半軸齒輪而言，齒面失效后，嚴重影響轉向機構的壽命。眾所周知，在汽車完成曲線行駛路段時，差速器的穩定運轉直接關系整車的安全轉向，當汽車在曲線行駛路段變化轉向時，行星齒輪和半軸齒輪接觸表面的速度發生明顯的變化，2個表面的速度差必然發生變化，整個過程中的潤滑狀況比較復雜，因此對行星齒輪和半軸齒輪表面摩擦和磨損的管控至關重要。差速器錐齒輪并不總是經常處于嚙合狀態，當汽車轉彎或左右輪行駛不同路程時，或一側車輪打滑而滑轉時，差速器行星齒輪才會發生相對運動。差速器錐齒輪常見的失效形式主要有齒輪齒面剝落、磨損、斷裂、表面點蝕等，如果行星齒輪和半軸齒輪齒面潤滑不當，齒面之間不易形成油膜，齒面直接接觸會造成齒面的剝落。因此，研究差速器錐齒輪差速工況下的摩擦和磨損機制具有實際意義。

國內對汽車差速器錐齒輪的運動學及動力學分析研究較多，多從有限元的角度去研究錐齒輪的摩擦和磨損，且多從靜態的角度去研究錐齒輪的運動特性。周新建等[2]闡述了差速器的傳動原理，利用ADAMS建立了差速器齒輪結構的虛擬樣機模型，并對該機構進行了2種工況下的仿真分析，得到傳動齒輪的轉速特性曲線及受力曲線，并通過對曲線分析了差速器的差速原理。張利鵬和祁炳楠[3]研究了差速器各部件之間的相互作用關系和半軸齒輪的差速機制，對其進行了受力分解和內摩擦力矩的計算，并對其轉矩轉速分配特性進行了建模。馬駿[4]分析了汽車驅動輪和差速器行星齒輪的受力情況，闡述了對稱式錐齒輪差速器實現差速的動力學原理。王良模等[5]運用現代方法分析了某汽車差速器齒輪靜強度并預測其疲勞壽命，根據齒輪的對稱性，建立了行星齒輪和半軸齒輪單齒的有限元模型。肖文穎和王書翰[6]對錐齒輪差速器的動力學進行了詳細分析，根據差速器齒輪的力矩分配情況分析了差速器內摩擦對差速器鎖緊系數的影響。付凱等人[7]提出了一種汽車差速器嚙合效率的計算方法，選用直齒輪積分法嚙合效率公式，將直齒錐齒輪等效為當量直齒圓柱齒輪，建立了一對定軸直齒錐齒輪的效率公式。馮海生等[8]研究了變工況對齒輪傳動系統動特性影響，基于彈塑性接觸理論，給出一種可以考慮變工況沖擊、嚙入沖擊、節點沖擊的齒輪接觸碰撞力參數預估算法，并結合多體動力學軟件建立柔性齒輪傳動系統動力學模型。鮑培德等[9]基于彈性流體動力潤滑理論，針對行星齒輪變速器內齒輪主動和太陽輪主動的2種工況，分別求出行星齒輪與太陽輪嚙合以及與內齒輪嚙合時，沿嚙合線在嚙合點的最小油膜厚度。李海鵬等[10]基于有限元動態仿真方法，建立差速器齒輪接觸有限元模型，進行動態嚙合仿真，研究了齒輪嚙合時的應力分布情況。目前，國外相關學者對差速器的研究多集中于設計特征和運動分析[11-16]。本文作者基于多重網格法和多重網格積分法，對差速器錐齒輪建立時變彈性流體動力潤滑模型，并針對差速工況，研究了行星齒輪和左右半軸齒輪的潤滑特性。

1 差速器齒輪轉矩及轉速分配

研究對象為對稱式圓錐齒輪差速器，差速器結構如圖1所示，其半軸齒輪和行星齒輪主要參數如表1所示。

圖1 差速器結構示意圖

表1差速器錐齒輪相關參數

Table1Theparametersofdifferentialbevelgear

參數行星齒輪左右半軸齒輪齒數zz1=10 z2=16壓力角α22.5°22.5°模數mm1=3.74 mm m2=3.74 mm節錐角ψ32°58°外錐距R35.291 mm35.291 mm節圓直徑dd1=37.4 mm d2=58.6 mm齒頂圓直徑dada1=43.91 mm da2=60.87 mm齒頂圓直徑df df1=32.55 mm df2=53.78 mm齒寬bb1=10 mm b2=10 mm

差速器中殼體與齒輪的轉矩關系如下：

T0=T1+T2

(1)

Tr=T2-T1

(2)

(3)

式中:T0是輸入扭矩;T1和T2分別是左右半軸扭矩；Tr是內摩擦扭矩。

差速器中半軸齒輪、行星齒輪的轉速關系為

n1+n2=2n0

(4)

(5)

式中：n1和n2分別是左右半軸齒輪的轉速；n0是差速器殼體的轉速；n3是行星齒輪的轉速；r2和r3分別是半軸齒輪節圓半徑和行星齒輪節圓半徑。

通過差速器的轉速和轉矩特性方程，可以得到差速器轉速和轉矩分配情況[3]。圖2所示是差速器左右半軸齒輪的轉速曲線，圖3所示是差速器輸入扭矩曲線，圖4所示是差速器轉矩分配結果，圖5所示是差速器轉矩分配比。

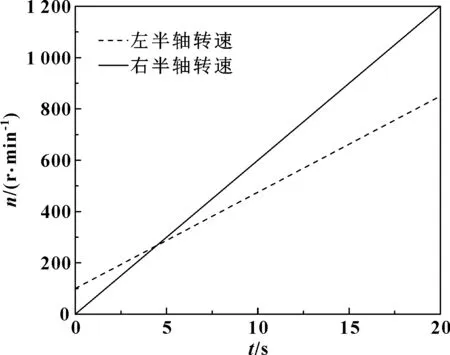
圖2 左右半軸齒輪轉速隨時間的變化

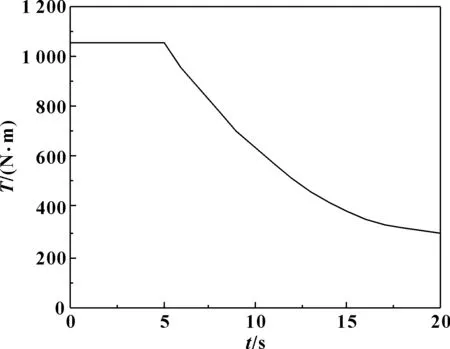
圖3 輸入扭矩隨時間的變化

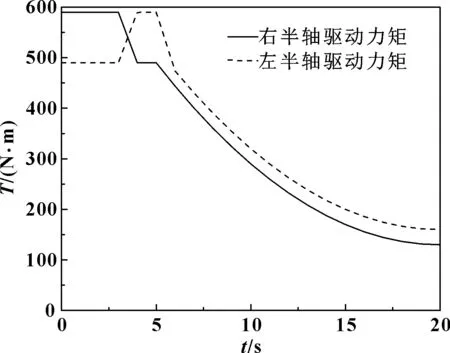
圖4 差速器轉矩分配結果隨時間的變化

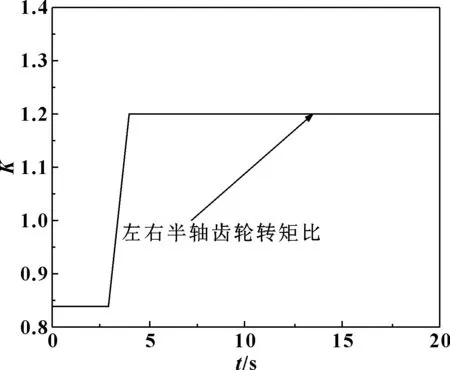
圖5 差速器轉矩分配比隨時間的變化

由圖2可知，起始階段左半軸齒輪轉速大于右半軸齒輪轉速，在第3 s左右出現轉速相同的情況，隨后右半軸齒輪轉速增長幅度大于左半軸齒輪轉速增長幅度。由圖3可知，差速器輸入轉矩在5 s之內保持不變，隨后輸入轉矩逐漸減小。由圖4可知，起始階段分配給左半軸齒輪的驅動力矩小于右半軸齒輪的驅動力矩，隨后左半軸齒輪的驅動力矩開始大于右半軸齒輪的驅動力矩。由圖5可知，起始階段差速器左右半軸齒輪驅動力矩分配系數略小，隨后分配系數穩定在1.2附近。

2 數值分析

以汽車差速器為研究對象，結合實際工況，分離出汽車差速器行星齒輪和半軸齒輪，建立時變無限長線接觸彈性流體動力潤滑模型。等效模型圖如圖6所示。

表2給出了數值分析中涉及到的潤滑劑和材料基本參數。

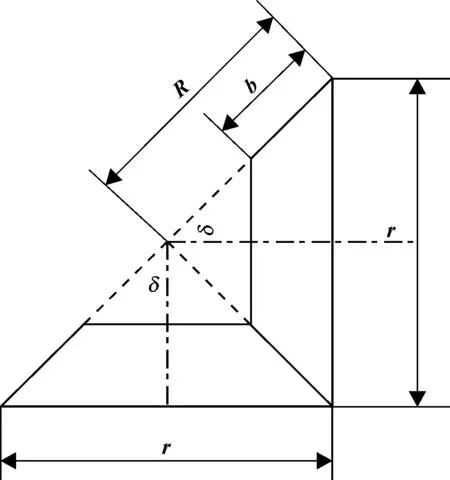
圖6 直齒圓錐齒輪的接觸等效圖

表2基本參數

Table2Basicparameters

參數數值潤滑油的環境黏度η0/(Pa·s)0.08黏壓系數α/Pa-12.19×10-8齒輪的彈性模量E/GPa210泊松比μ0.3

2.1 Reynolds方程

(6)

式中：x為坐標變量；p為油膜壓力(Pa)；h為油膜厚度(m)；ρ為潤滑油密度(kg/m3)；η為潤滑油黏度(Pa·s)；u為卷吸速度(m/s)。

2.2 膜厚方程

(7)

式中：h0為中心膜厚(m)；R為輪齒在嚙合點處兩齒廓的綜合曲率半徑(m)；E為兩輪材料的綜合彈性模量(GPa)。

2.3 黏壓關系

η=η0exp{(lnη0+9.67)[(1+5.1×10-9p)z0-1]}

(8)

式中：η0為潤滑劑環境黏度(Pa·s)；z0為Roelands黏壓系數。

z0=α/[5.1×10-9(lnη0+9.67)]

(9)

2.4 密壓關系

密壓關系采用Dowson-Higginson公式

(10)

2.5 載荷方程

記w為單位長度上的載荷(N/m)，則壓力應該滿足載荷方程：

(11)

3 直線轉曲線行駛差速工況下的潤滑特性分析

如圖7所示，差速器由直線行駛工況向差速工況過渡時，行星齒輪與左右半軸齒輪的轉速和轉矩均發生瞬時變化，差速工況下的行星齒輪與半軸齒輪進入嚙合狀態，兩齒面開始發生相對滑動；相對直線行駛工況，行星齒輪需要承受較大的嚙合力。由于行星齒輪需要同左右半軸齒輪同時參與嚙合，故行星齒輪可以作為主要研究對象。圖8所示是直線行駛工況和差速工況下行星齒輪與左半軸齒輪嚙合時的中心膜厚分布。圖9所示是2種不同工況下的滑滾比變化。圖10所示是差速工況下行星齒輪分別與左右半軸齒輪嚙合時的中心壓力。圖11所示是差速工況下行星齒輪分別與左右半軸齒輪嚙合時的最小油膜厚度。

圖7 直線行駛工況轉差速工況

圖8 直線行駛工況和差速工況下的中心膜厚分布

圖9 直線行駛工況和差速工況下的滑滾比Δs變化

圖10 差速工況下行星齒輪分別與左 右半軸齒輪嚙合時的中心壓力

圖11 差速工況下行星齒輪分別與左 右半軸齒輪嚙合時的最小膜厚

圖12所示是差速工況下行星齒輪分別與左右半軸齒輪嚙合時的最大壓力。圖13所示是差速器行星齒輪的滑動速度。圖14所示是左右半軸齒輪的滑動速度。圖13和圖14中的滑動速度是量綱一化滑動速度，該滑動速度用來表征行星齒輪和左右半軸齒輪的滑動趨勢。

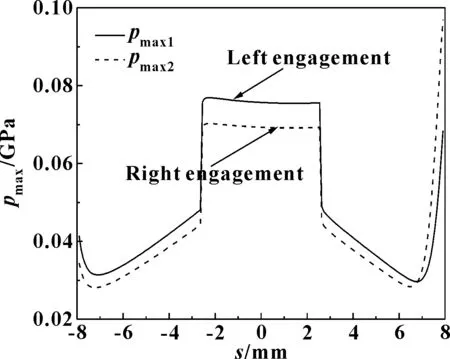
圖12 差速工況下行星齒輪分別與左 右半軸齒輪嚙合時的最大壓力

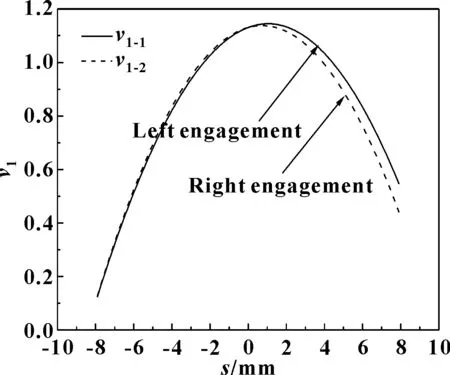
圖13 差速工況下行星齒輪分別與左 右半軸齒輪嚙合時的滑動速度

圖14 差速工況下左右半軸齒輪的滑動速度

由圖8可知，在直線行駛工況下，中心油膜厚度在整個嚙合區間呈現出增加的趨勢；在差速工況下，中心油膜厚度在整個嚙合區間呈現出減小的趨勢，且差速工況下的中心油膜厚度相比直線行駛工況下的中心油膜厚度較小。由圖9可知，差速工況下的滑滾比相對直線行駛工況下的滑滾比較大，通過2種工況滑滾比對比可知，差速工況下行星齒輪與半軸齒輪的齒面滑動相對較大。 由圖10可知，行星齒輪與左右半軸齒輪嚙合的中心油膜壓力在整個嚙合區間有所不同，在嚙入區間，行星齒輪與左半軸齒輪嚙合時的中心油膜壓力大于行星齒輪與右半軸齒輪嚙合時的中心油膜壓力，越過嚙入區間后，行星齒輪與左右半軸齒輪嚙合時的中心油膜壓力先減小后增加。由圖11可知，行星齒輪同右半軸齒輪在嚙入區間的最小油膜厚度大于行星齒輪與左半軸齒輪在嚙入區間的最小油膜厚度。

圖13和圖14分別反映的是行星齒輪和左右半軸齒輪的速度變化，由圖13可知，行星齒輪同左右半軸齒輪嚙合時的齒面滑動速度均為先增大后減小的趨勢。由圖14可知，左右半軸齒輪齒面滑動速度在差速工況下逐漸較小，由差速器轉速方程可知，差速器左右半軸齒輪的轉速變化同行星齒輪的轉速變化無關。

在差速工況下，行星齒輪發生自轉，同時與左右半軸齒輪參與嚙合，行星齒輪齒面同左右半軸齒輪齒面發生相對滑動，行星齒輪和半軸齒輪的轉速發生變化，當差速器由直線行駛工況轉向差速工況時，行星齒輪的轉速發生瞬時變化，左右半軸齒輪的轉速變化不同，右半軸齒輪的轉速大于左半軸齒輪的轉速，其轉矩也隨之發生變化。

4 曲線行駛路段差速變工況下的潤滑特性分析

曲線行駛路段差速變工況分為2個部分，其一是直線行駛工況過渡到左轉彎工況，其二是左轉彎工況過渡到右轉彎工況。圖15所示是曲線行駛路段變工況簡圖。

圖15 曲線行駛路段變工況

圖16所示是2個工況下同左半軸齒輪嚙合的行星齒輪齒面量綱一化滑動速度，圖17所示是2個工況下行星齒輪與左半軸齒輪嚙合時的最小油膜厚度變化。圖18所示是2個工況下行星齒輪與左半軸齒輪嚙合時的最大壓力變化。其中第一個工況是左轉彎工況，第二個工況是右轉彎工況。

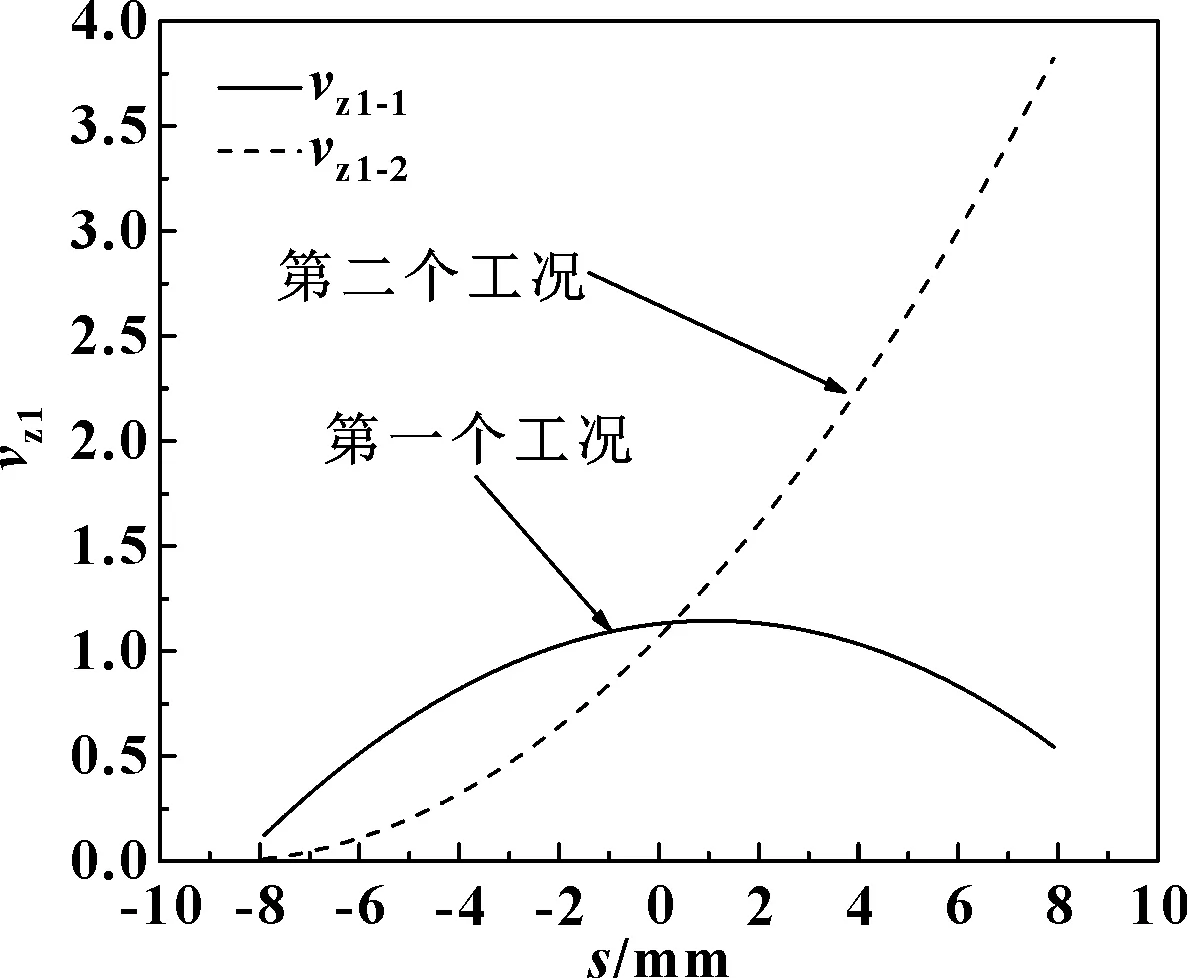
圖16 變工況下行星齒輪的滑動速度

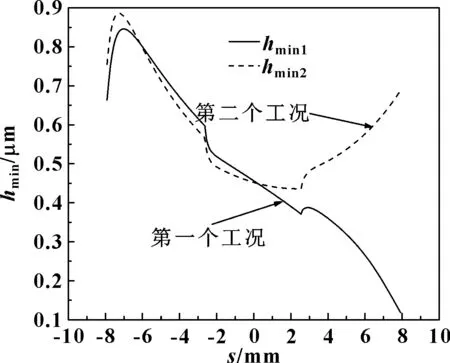
圖17 變工況下行星齒輪與左半軸齒輪嚙合時的最小油膜厚度

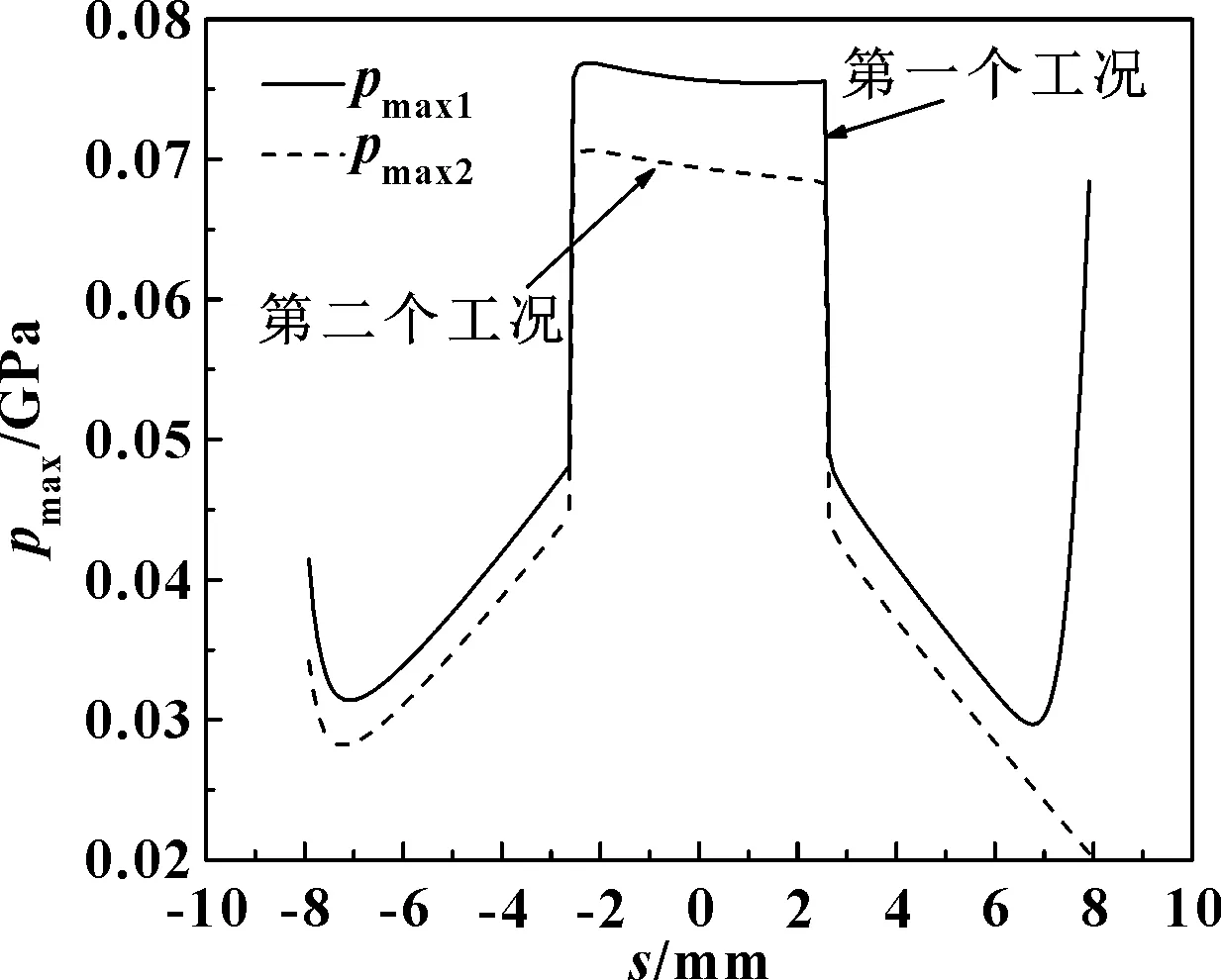
圖18 變工況下行星齒輪與左半軸齒輪嚙合時的最大壓力

由圖16可知，在開始進入嚙入區間時，第一個工況下的行星齒輪齒面滑動速度比第二個工況下的行星齒輪齒面滑動速度大，伴隨著行星齒輪與左半軸齒輪的嚙合，第一個工況下的行星齒輪齒面滑動速度逐漸減小，而第二個工況下的行星齒輪齒面滑動速度逐漸增大。由圖17可知，第二個工況下行星齒輪與左半軸齒輪嚙合的最小油膜厚度，大于第一個工況下行星齒輪與左半軸齒輪嚙合的最小油膜厚度。由圖18可知，第二個工況下行星齒輪與左半軸齒輪嚙合的最大油膜壓力，小于第一個工況下行星齒輪與左半軸齒輪嚙合的最大油膜壓力。

5 結論

(1)當差速器由直線行駛工況進入差速工況時，行星齒輪同半軸齒輪嚙合時的中心膜厚減小，行星齒輪同半軸齒輪嚙合時的滑滾比增大，兩齒面發生較大的相對滑動。

(2)差速工況時行星齒輪同左半軸齒輪嚙合時的最小油膜厚度和最大油膜壓力，明顯有別于行星齒輪同右半軸齒輪嚙合時的最小油膜厚度和最大油膜壓力，由于左轉彎工況下的左半軸齒輪轉速小于右半軸齒輪轉速，而速度對最小油膜厚度的影響較大，所以在整個嚙合區間行星齒輪同左右半軸齒輪的潤滑狀況有所不同。

(3)差速變工況下的左右半軸齒輪的轉速發生變化，當由第一個工況轉入第二個工況時，行星齒輪的轉速逐漸增大，此時行星齒輪與左半軸齒輪的相對滑動加劇，行星齒輪與左半軸齒輪嚙合時的最小油膜厚度瞬時增大。