二維板條梁模型水彈性計算
薛繼陽 熊鰲魁 桑騰蛟
(武漢理工大學交通學院 武漢 430063)
0 引 言
超大型浮體大尺度、小剛度的特點,導致結構在外載荷的作用下的彈性變形比較重要.相對于傳統將結構物作為剛體計算結構物的運動就不能很好的預測超大型浮體結構的變形,必須在考慮結構物剛體運動的同時考慮到結構的彈性體變形.關于超大型浮體結構的變形計算的兩種思路:①利用模態疊加法,即將彈性體的變形位移由很多運動模態疊加而成,然后分別計算各個模態所對應的水動力,最終帶入運動方程求解位移;②直接將結構位移進行離散處理,將結構的振動方程作為邊界條件進行求解.而對于流場的計算,同樣存在格林函數和特征函數匹配兩種方法.其中格林函數法是在邊界上分布滿足控制方程的格林函數,通過滿足相應的邊界條件求解邊界上分布格林函數的源強求解速度勢.而特征函數則是通過匹配其他邊界條件求解級數系數從而得到速度勢.
Newman[1]對模態疊加法求解水彈性問題進行了詳細的敘述.Chong等[2]則利用模態疊加法對考慮吃水的平板,并且入射波帶有一定的入射角的水彈性問題進行了具體分析.Kim等[3]則對利用特征函數匹配方法求解水彈性問題進行了相應研究.Wu等[4]同樣采用模特疊加方法,其中采用了邊界元積分方法去求解散射勢和輻射勢,Ohmatsu[5]利用板的振動方程導出來修改后的自由表面邊界條件,導出新的色散關系,類比與光學中的折射定律導出了結構彈性波波幅的傳遞函數,隨后進一步對時域、拖曳情形(存在一定的航速)、裝配組合情形,以及超大型浮體系泊風險分析進行了進一步的討論.金晶哲等[6]比較了求解水彈性問題的模態展開法及特征函數展開法,表明兩種方法基本上可以比較準確地預報浮體結構的撓曲變形,模態函數展開方法與試驗結果吻合得略好,特征函數展開方法在某些波長下給出的預報結果與試驗數據還有一定的差距.閆紅梅[7]根據文獻[8]提出的一種矩形平板的撓度函數進行超大型浮式結構物在波浪中的水彈性響應分析,提出了一種滿足板振動方程的平板格林函數,將平板的位移用壓力分布函數與平板格林函數表示,而根據伯努利公式將壓力表達成速度勢的函數,即可求解流場的速度勢.
1 基本理論
對于大型浮體在線性波浪下的水彈性問題,由于其水平尺度比較大.故將其簡化成平面問題考慮,見圖1.其中入射區及透射區均存在級數解.假定流體為理想無旋流體,中間計算域速度勢滿足Laplace方程,而計算域與入射區和透射區的邊界1和邊界2均滿足速度勢及法向速度連續,邊界3即底面邊界條件,滿足物面不可穿透邊界條件,而邊界4即為兩端自由的梁,滿足梁的振動方程,同時滿足速度連續.根據控制方程以及邊界條件即可對中間計算域的流場進行求解.

圖1 計算模型圖
入射區的速度勢函數為
(1)
式中:H為波高;ω為波浪圓頻率;g為重力加速度;k為波數;d為水深;a為平板半長;Ap,Kp為相應的常數.
速度勢對于x的偏導為
(2)
設定計算域的速度勢函數為Φ,則在邊界1滿足速度勢及速度勢法向導數連續.
(3)
利用速度勢特征函數的正交性,得到邊界1上的邊界條件為

(4)
(5)
透射區域速度勢級數解為
(6)
在邊界2上仍然滿足速度勢以及速度勢法向導數連續,處理方式與邊界1類似,得到邊界2上的邊界條件為

(7)
(8)
邊界3為水底滿足物面不可穿透邊界條件,即在邊界3上有
(9)
邊界4忽略了板的吃水,將其簡化為兩端自由的梁,滿足梁的振動方程
(10)
式中:E為材料的彈性模量;I為梁截面的慣性矩;S為截面面積;ρ為材料密度;P為梁上的作用壓力.并且滿足梁兩端偏移量的兩階導和三階導等于0,物理含義為自由梁兩端的力矩以及剪力為0.
2 數值方法
建立起控制方程和邊界條件之后,即建立離散模型對方程進行求解.首先對計算域離散劃分為相應的四邊形網格,見圖2.

圖2 中心網格離散
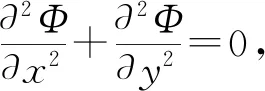
(11)
得對于計算域中心的每個節點都有對應的方程,但對于邊界上的節點無法提供方程,必須利用相應的邊界條件補充方程使得方程組封閉得以求解.這里采用的方法是將邊界上的節點再外推一排,則原始邊界上的節點即可利用控制方程給出相應的離散方程,而新增加的節點必須利用邊界條件給出新的方程.
對于邊界1,該邊界條件為第三類邊界條件,見圖3.
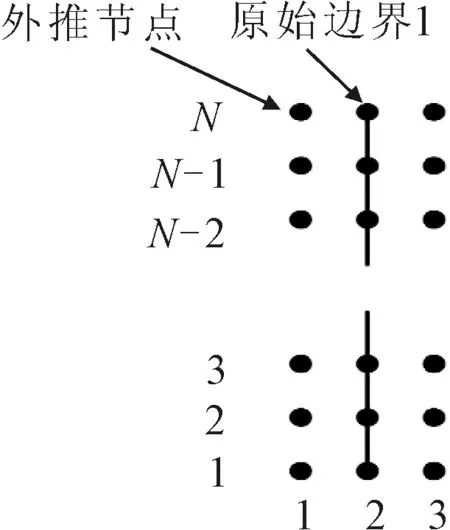
圖3 邊界1離散

對于梯形積分兩端的端點值取一半:即有A11=ikcosh (k(z1+d))·dz/2,B11=cosh (k(z1+d))·dz/2;A1N=ikcosh (k(zN+d))·dz/2,B1N=cosh (k(zN+d))·dz/2.
對于速度勢偏導采用的中心差分格式即:Φxi2=(Φi3-Φi1)/2dx.
對于式(5)是一個齊次方程,即當j>1,bj=0.且有:Api=kpcos (kp(zi+d))dz,Bpi=-cos (kp(zi+d))dz;Ap1=kpcos (k(z1+d))·dz/2,Bp1=-cos (kp(z1+d))dz/2;ApN=kpcos (k(zN+d))·dz/2,BpN=-cos (kp(zN+d))dz/2.
邊界2的處理方式與此類似,這里不在詳述.
對于邊界3和邊界4的處理方式比較類似,不同的邊界3上的法向速度為0,而邊界4上的法向速度由梁的振動解指定.采用的方式任然是采用外推一排節點,見圖4.

圖4 邊界3離散
由此可以提供邊界3上的M個方程.

3 模型驗證


圖5 固壁受力級數解與計算結果對比
同樣參數下對應平板作升沉運動時的輻射力見圖6.
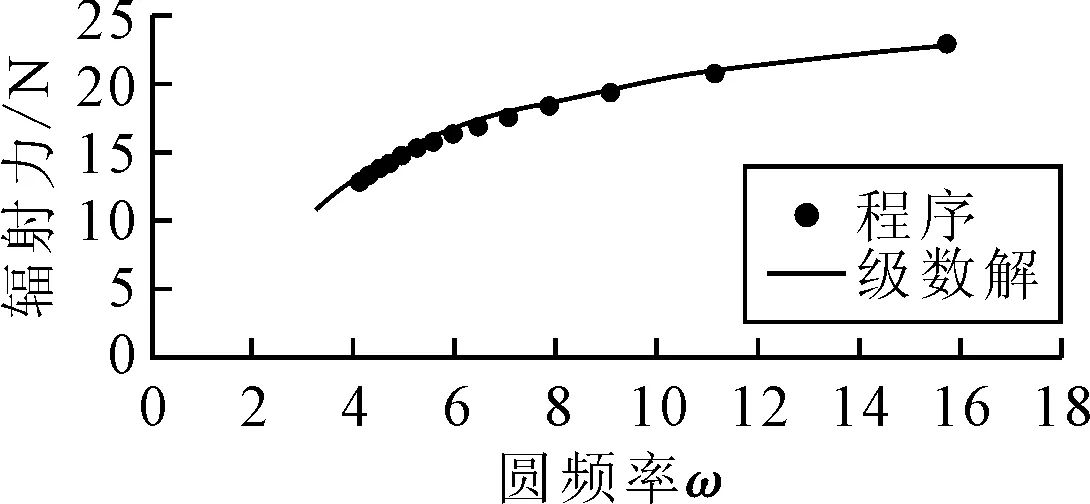
圖6 輻射力級數解與計算值對比
由圖5~6可知,通過差分匹配邊界條件求解場方程得到的結果與相應的級數解十分接近,證明了該方法的可靠性,下面即用此來研究平面梁板模型的水彈性行為.
4 梁板模型水彈性計算結果


圖7 不同波長板長比下板梁模型位移與三維實驗值比較
5 結 束 語
文中將超大型浮體結構的水彈性問題忽略吃水之后將其簡化為兩端自由的板條梁的水彈性問題,由于未考慮試驗室一側的牽引以及忽略了吃水導致計算結果一側與試驗有一定的差別,但是另一端自由端的計算結果與實驗值比較一致.并且在波長板長比在比較大的情況下結果與試驗比較一致.

