基于貝葉斯網絡的地鐵牽引變電所可靠性分析

何江海，裴衛衛，閆雅斌，魯曉珊，邢宗義

（1. 廣州地鐵集團有限公司，廣州 510308；2.南京理工大學 自動化學院，南京 210094）

地鐵因其運輸量大、節能環保、快速安全和準時性好等優點，成為城市軌道交通發展的重要方向，是目前緩解大中型城市交通擁擠的主要方式[1]。城市地鐵線路的快速發展極大地方便了民眾的日常出行，與此同時，地鐵牽引供電系統的安全可靠運行也面臨著新的挑戰。

目前，國內外學者對牽引供電系統的可靠性研究已經取得諸多進展，其主要研究對象集中在鐵路的交流牽引供電系統[2]；而對于地鐵牽引供電系統可靠性研究方面，因其系統主接線形式、運行方式和供電方式等均與鐵路牽引供電系統存在差異，因此，也有許多學者對其展開深入研究。其中，李想結合可靠性框圖法和故障樹法對地鐵接觸網展開了綜合分析[3]；曾德容通過故障模式與影響分析法和故障樹法相結合，對地鐵牽引供電系統展開可靠性研究，提出了系統故障數據的預測方法，進一步豐富了該領域的可靠性研究[4]。曹景雷采用GO法分別構建了地鐵牽引變電所和架空接觸網的可靠性模型，并對其中的供電網絡和一段供電區間進行了可靠性計算，采用層次分析法對地鐵接觸網的主要設備展開可靠性分配[5]。徐浩結合故障樹和貝葉斯網絡各自在建模和計算過程中的優勢，簡化了基于故障樹分析法的計算復雜度，對地鐵牽引變電所頂事件的失效概率及各節點的后驗概率進行定量計算。但是，以上研究沒有考慮牽引變電所不同的運行方式和故障模式對可靠性模型結構造成的影響[6]。

本文基于貝葉斯網絡，通過GeNIE仿真軟件計算地鐵牽引變電所（簡稱：變電所）可靠性模型頂事件的故障率，并采用聯合樹推理算法對變電所的網絡模型展開推理計算，得到各個節點的后驗概率排序，定量地識別出變電所的薄弱環節；同時，基于動態貝葉斯網絡建立變電所的可靠性模型，并在時間維度上對該模型展開計算，得到了變電所隨時間變化的故障率曲線及后驗概率排序等，進而得到影響變電所穩態可靠性的主要因素，為變電所監測與設備維護提供理論支撐。

1 貝葉斯網絡

1.1 貝葉斯網絡的基本原理

貝葉斯網絡采用有向圖的方式表述系統變量間的概率關系，解決系統各元件因條件相關性而引起的不確定性問題[7]。在實際應用中，貝葉斯網絡可以利用概率論和圖論方法系統地描述隨機變量之間的關系，進而從不完整的或者不精準的信息中做出推理和判斷；同時，貝葉斯網絡還可以方便地進行概率推理，即計算各事件發生時系統各元件的后驗概率情況。

1.1.1 貝葉斯網絡概率論基礎

概率論是貝葉斯網絡理論發展的基礎，在利用貝葉斯網絡理論進行計算推理時常用的概率論知識包括：條件概率、貝葉斯公式、先驗概率、后驗概率以及條件獨立等[8]。

設事件集合E，B為事件集合的樣本數據，且B={Bi,B2, …,Bn}是一個相互獨立的事件組，P(Bi)＞0，A是E中的任意事件，則貝葉斯公式如式（1）所示。

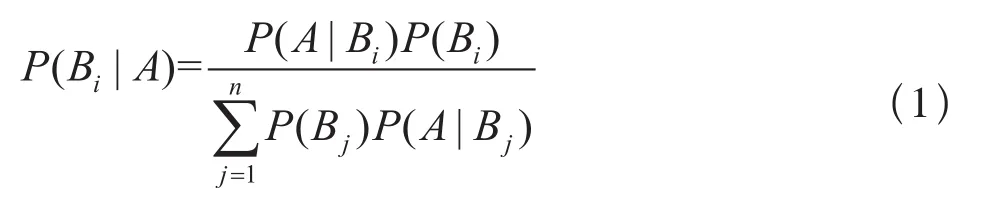
式（1）中，P(Bi)表示先驗概率，一般由專家分析判斷或者根據現有歷史統計數據計算得到，是網絡中的初始概率值；P(Bi|A)表示后驗概率，可以由元件先驗概率經貝葉斯公式修正以后得到；P(A/Bi)表示條件概率，表示在事件Bi發生的條件下，事件A也發生的條件概率。

1.1.2 貝葉斯網絡圖形描述

貝葉斯網絡圖形主要是由節點和有向邊組成的有向無環圖，其中，節點包括根節點、葉節點以及中間節點3種類型，分別代表系統中不同的隨機變量，而連接各節點的有向邊則表示節點間的邏輯關系；同時，父節點與子節點之間的邏輯關系可以用條件概率表表示。

圖1是一個貝葉斯網絡的圖形表示，包含4個節點和4條有向邊。圖中，P(C=1)=0.4，表示節點C的先驗概率，而節點B、D、S標注的是條件概率表。

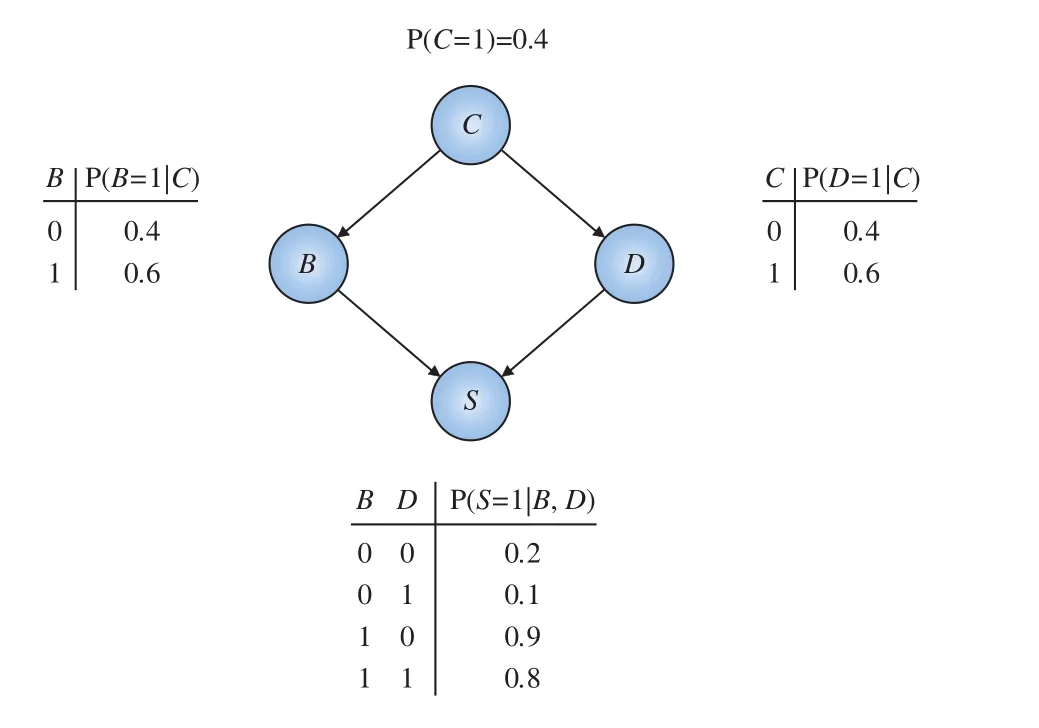
圖1 貝葉斯網絡的圖形表示

1.1.3 貝葉斯網絡推理算法

貝葉斯網絡推理是根據節點的先驗概率和條件概率表計算某一事件發生的概率。在可靠性分析的理論應用中，貝葉斯網絡的優勢在于其可以進行雙向推理，即可以利用父節點和子節點之間的互相關系，由上到下由故障原因得到推斷結果，也稱因果分析；也可以自下而上推理得到系統故障時各節點的后驗概率，從而推測出系統故障的原因，該方法也稱致因推理或診斷推理。貝葉斯網絡推理算法包括精確推理算法和近似推理算法兩類，其中，精確推理算法用于系統結構較小的貝葉斯網絡，主要包括組合優化方法、全局聯合推理算法、團樹傳播算法等。近似推理算法用于網絡結構中節點數量較多的大型貝葉斯網絡，以此來解決節點數量過多引發的計算量過大問題，主要包括基于搜索的方法、隨機模擬方法等。

在貝葉斯網絡推理過程中，選擇合理的推理算法可以提高推理速度和結果精度。其中，團樹傳播算法的推理結果精確、計算效率高、具有較強的靈活性和適應性，是目前常用的一種精確推理算法。

1.2 動態貝葉斯網絡基本原理

動態貝葉斯網絡是在靜態貝葉斯網絡的基礎上對引入時間問題的拓展，在繼承了貝葉斯網絡分析推理優勢的同時，將靜態的網絡結構拓展到時間維度，形成了可以解決時序問題的網絡模型[9]。

1.2.1 動態貝葉斯網絡表示

在用動態貝葉斯網絡描述動態系統的隨機模型時，需要得到系統隨機變量X[1]，……，X[n]的聯合概率分布。因此，在研究復雜動態系統模型時，需要基于平穩假設和馬爾可夫假設兩個約束條件來簡化處理，則動態貝葉斯網絡描述的隨機過程聯合概率分布可以由靜態的初始網絡和轉移網絡兩部分組成[10]。

初始網絡B0表示事件在初始狀態X[0]下的聯合概率分布。轉移網絡B→表示事件在X[t-1]，X[t]，t=1, 2, …,n下的轉移概率分布，記作P(X[t]|X[t-1])。則給定動態貝葉斯網絡模型B*(B0,B→)的初始網絡和轉移網絡，其隨機變量X[1], …,X[n]的聯合概率分布可以表示為：

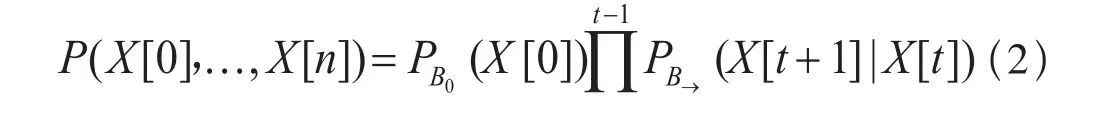
由式（2）可知，動態貝葉斯網絡模型描述了系統在動態隨機過程中時間軌跡上的概率分布情況，圖2是一個簡單動態貝葉斯網絡的圖形表示。

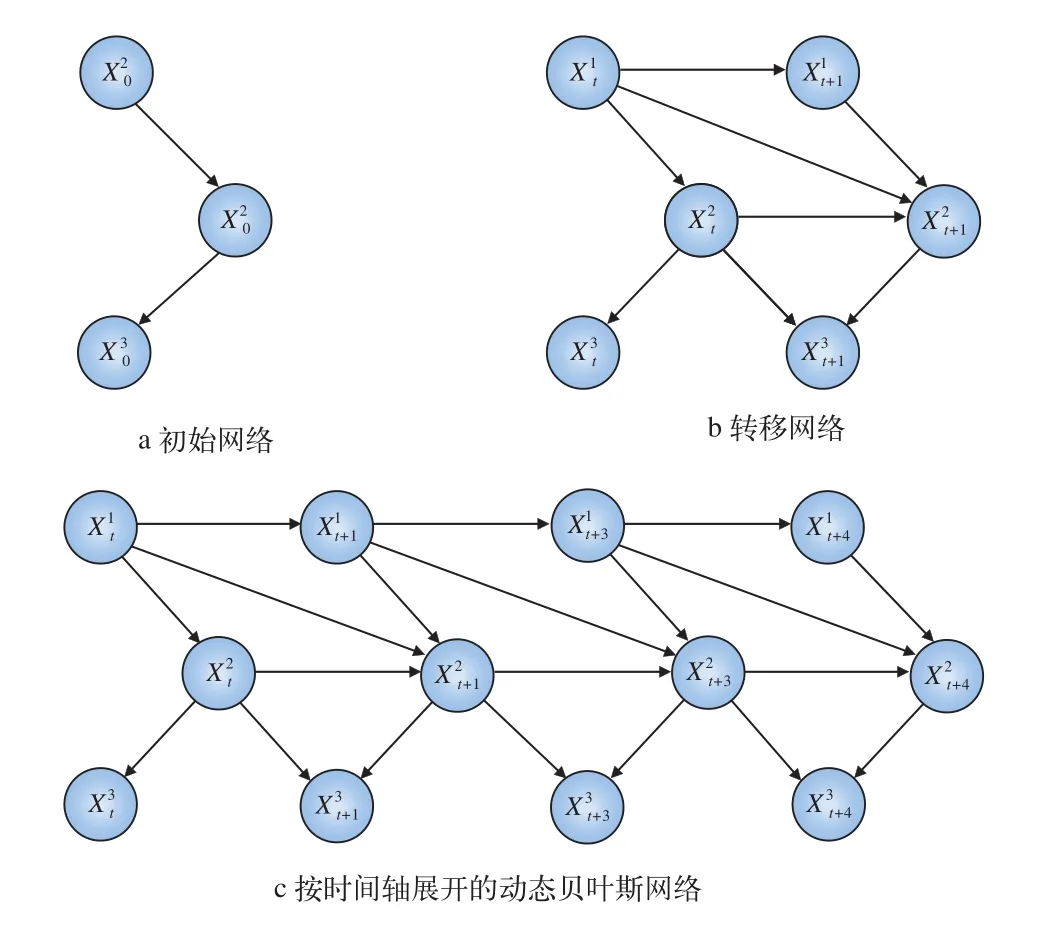
圖2 動態貝葉斯網絡示意圖

1.2.2 動態貝葉斯網絡推理算法

理論上，動態貝葉斯網絡推理可以通過不斷復制時間片的方式展開，利用靜態貝葉斯網絡對其容納的所有觀察序列進行推理。然而，如果當動態貝葉斯網絡所要觀察的時間比較長時，通過不斷復制時間片展開的動態貝葉斯網絡結構在計算時需要消耗更多的存儲空間；此外，隨著新的觀察序列加入，動態貝葉斯網絡只是簡單地重復上述運算過程，每次觀察序列的更新也需要較長的運算時間，所以，這類方法計算復雜度較高，并且極大地浪費系統資源。國內外學者通過對動態貝葉斯網絡特殊結構的處理設計了一些優化算法，其中，代表性算法包括：（1）動態精確推理算法，如1.5片聯合樹推理算法、邊界（F）推理算法等；（2）動態近似推理算法，如BK推理算法、FF推理算法等。本文采用目前比較主流的1.5片聯合樹算法對變電所的穩態可靠性指標進行推理。

2 地鐵牽引變電所可靠性建模

在可靠性工程中，故障樹分析法是可靠性指標計算的常用方法，基于基本事件僅工作在正常和故障兩種狀態的假設，且通常所描述的事件之間有明確的邏輯關系。但是，對于多態系統和邏輯關系不明確的事件，該方法的應用就有一些局限。考慮到隨著變電所節點數量的增加，故障樹分析方法中最小路（割）集不交化算法比較復雜且計算量非常大，對于大型復雜網絡，一般只能求解近似值。貝葉斯網絡獨有的雙向推理既能夠對頂事件進行預測分析，又能夠方便地進行反向診斷推理，定量地計算出各單元在變電所中的重要程度，進而避免了故障樹分析法在尋找變電所最小（路）割集時的不交化過程，極大地提升了變電所可靠性分析的計算速度。因此，采用貝葉斯網絡建立變電所可靠性模型，能夠精確、快速地得到變電所的可靠性指標，同時，在考慮維修因素的情況下，建立變電所在時間維度上的動態貝葉斯網模型，進一步補充對變電所穩態可靠性的評價。

2.1 典型地鐵牽引變電所主接線

在對變電所進行可靠性研究時，既要考慮其結構組成以及運行方式，還需要充分了解變電所各元件可靠性模型及其故障形式的特性。歷史統計數據表明，對于不同類型的設備，其故障率的分布函數也有所不同，如果在構建變電所整個壽命周期的可靠性模型時分別采用不同的故障率分布函數，將會增加可靠性建模及分析的復雜度。綜合考慮到電力系統主要設備的故障率往往較低，而通過統計方法得到的可靠性參數誤差對變電所可靠性的影響可能會更大，本文根據變電所計算精度和復雜度的要求，以及某線路的實際情況，在計算過程中假設所有元件均處于壽命中期的偶然故障區，即失效率為常數，變電所元件的可靠度函數服從指數分布。

通常，在研究電力系統主要設備的可靠性時，假設這些為可修復元件，即某元件一旦發生故障就退出運行，待檢修完成后再恢復到正常工作狀態。同時，在計算過程中一般不考慮計劃檢修，而假設這些元件具有兩種狀態：正常工作狀態及故障狀態。

典型地鐵牽引變電所的主接線如圖3所示，其中，主要設備包括35 kV交流母線、交流斷路器、電動隔離開關、手動隔離開關、整流變壓器、整流器、直流母線和電流互感器等。同時，根據該牽引變電所的主接線形式，其運行方式可以分為正常運行方式和故障運行方式。

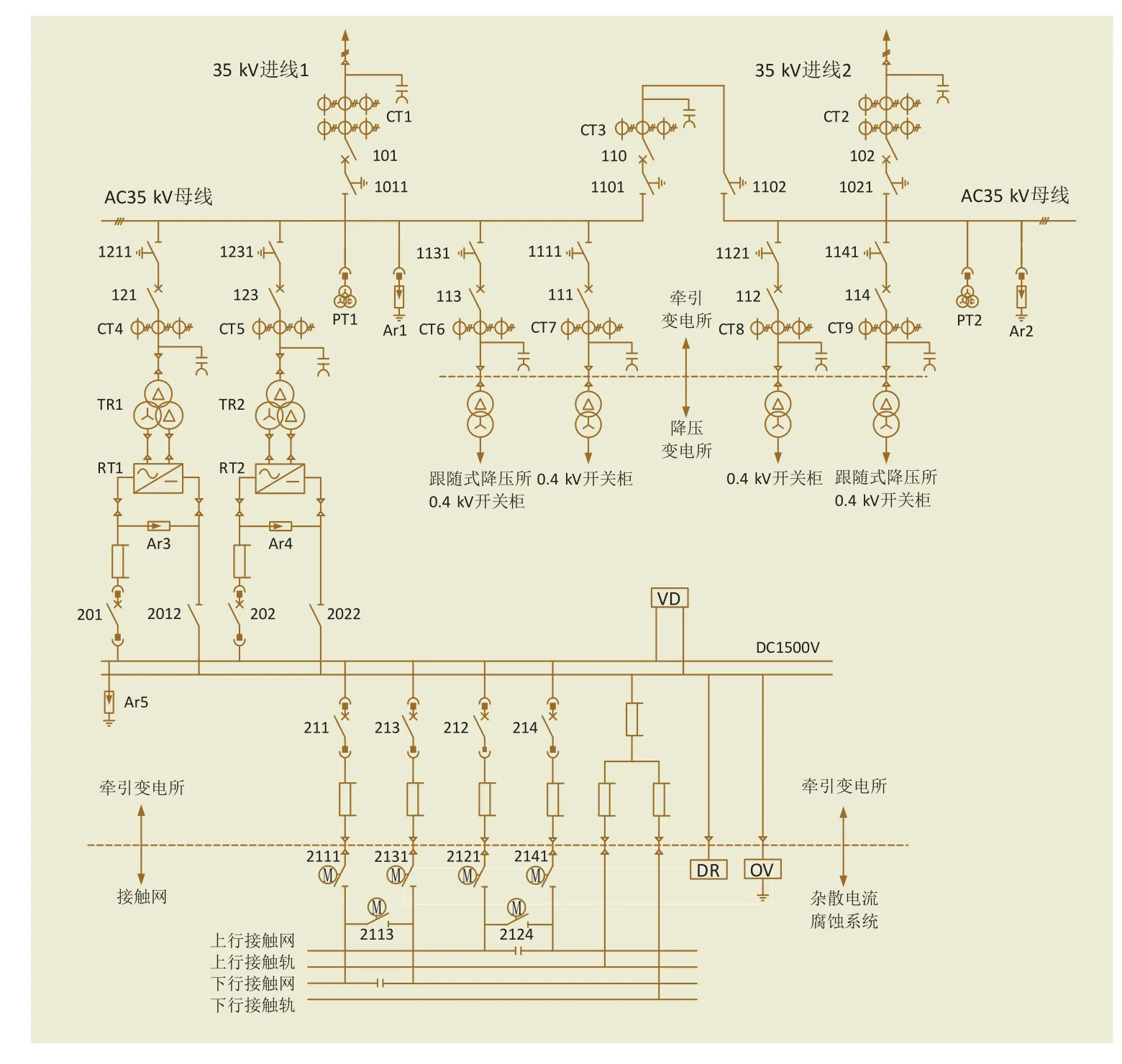
圖3 典型地鐵牽引變電所主接線圖

2.1.1 正常運行方式

正常運行方式下，變電所交流側為單母線分段形式，兩段母線分列運行，進線斷路器101、102合閘，分段斷路器110分閘；直流側兩套牽引整流機組接在同一段母線上并列運行，越區隔離開關2113、2124處于分閘位置。同時，該變電所通過接觸網與相鄰的牽引變電所構成雙邊供電。

2.1.2 故障運行方式

故障運行方式下，當一路引入電源退出運行時，分段斷路器110自動合閘，另一路引入電源負責該變電所牽引負荷和動力照明的一、二級負荷；當一套整流機組退出時，另一套整流機組在具備運行條件的情況下可以繼續運行，否則該變電所也退出運行；當直流側單臺饋線斷路器故障退出時，同一方向的縱向隔離開關合閘進行雙邊供電；當該變電所（不含終端變電所）故障退出時，由其相鄰的兩座牽引變電所通過越區隔離開關或者直流母線實行大雙邊供電，共同負責該區間的牽引負荷；當線路終端牽引變電所故障退出時，只能由相鄰的牽引變電所實行單邊供電，承擔該區間正常供電范圍內的牽引負荷。

2.2 典型地鐵牽引變電所的可靠性模型

2.2.1 貝葉斯網絡模型

貝葉斯網絡模型的構建方法：（1）在GeNIE軟件中，將圖3所示變電所主接線中的基本事件和邏輯關系轉換為貝葉斯網絡圖形中的節點；（2）根據地鐵牽引變電所基本事件之間的層次關系使用有向邊將貝葉斯網絡模型中的節點全部連接起來；（3）設置貝葉斯網絡中部分節點的條件概率表，并確定其它節點的先驗概率。最終得到典型變電所貝葉斯網絡的可靠性模型，如圖4所示。其中，各主要設備故障數據，如表1所示；模型中各個節點與基本事件的對應關系，如表2所示。

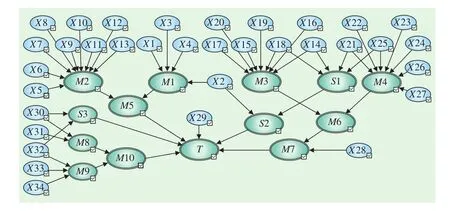
圖4 典型地鐵牽引變電所的貝葉斯網絡模型

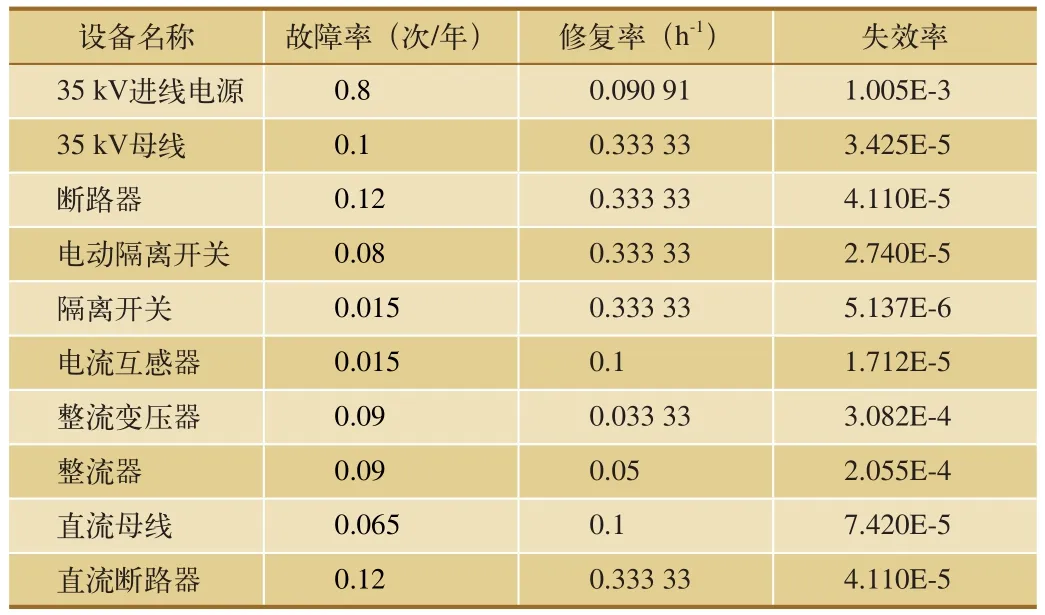
表1 牽引變電所各元件的故障數據

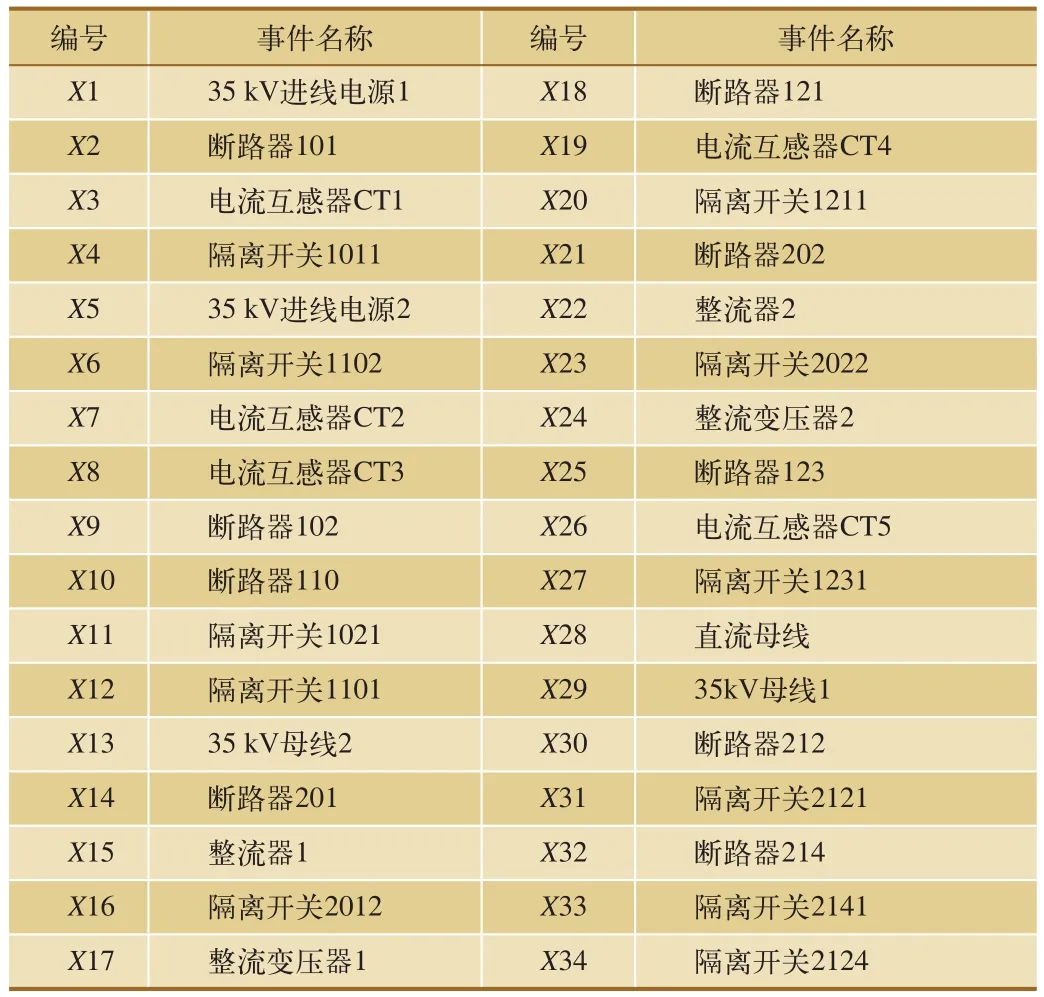
表2 貝葉斯網絡模型中各節點的含義

2.2.2 動態貝葉斯網絡模型

采用動態貝葉斯網絡建立變電所可靠性模型的方法與靜態貝葉斯網絡類似，主要包括圖形節點、有向邊、條件概率表、轉移概率表，以及先驗概率的設置等，不同之處在于動態貝葉斯網絡引入了時間因素，在網絡模型建立的過程中需要確定同一網絡節點當前時間與下一個單位時間之間的條件轉移概率。由于動態貝葉斯網絡基于平穩假設和馬爾可夫假設兩個約束條件，則：

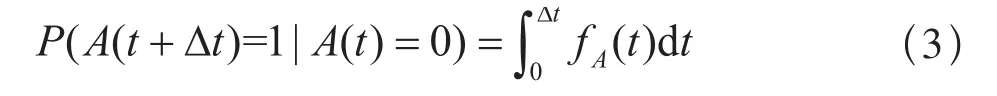
同時，動態貝葉斯網絡相鄰兩個時段之間的條件轉移概率可以表示為：

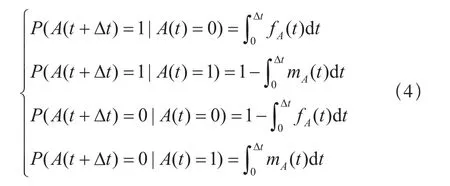
其中：1表示節點A失效；0表示節點A正常工作；fA(t)是節點A的失效密度函數；mA(t)是A的維修密度函數。則節點A當前時刻與下一時刻間的轉移概率表，如表3所示。

表3 節點A在相鄰時刻的轉移概率表

對于動態貝葉斯網絡，不僅需要對其靜態網絡進行賦值，還需要對其轉移網絡進行賦值，若假設變電所各主要設備的修復率和失效率均為常數，即設備壽命函數呈指數分布，則失效密度函數為f(t)=λe-λt、維修密度函數為m(t)=μe-μt。根據表3中轉移概率的計算過程，可以獲得動態貝葉斯網絡中各個節點的條件轉移概率表，其中，表4和表5分別是以節點X1為例的條件概率表和相鄰時刻的轉移概率表。

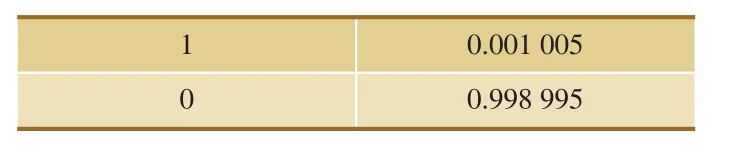
表4 節點X1在時間片內的條件概率表

表5 節點X1在相鄰時刻的轉移概率表

根據圖4所示的典型變電所貝葉斯網絡模型，在GeNIE軟件中構建其動態貝葉斯網絡，拓撲結構如圖5所示。其中，各節點的具體含義與靜態貝葉斯網絡節點相同。

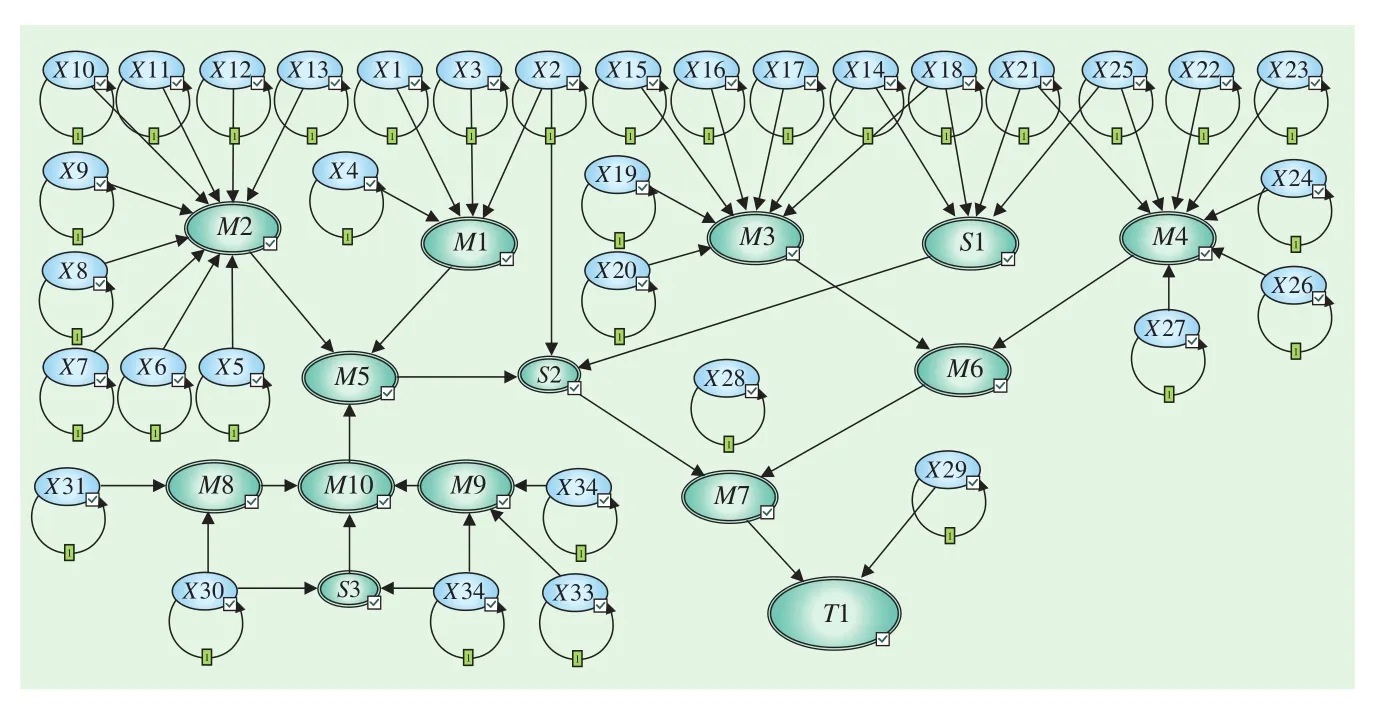
圖5 典型地鐵牽引變電所的動態貝葉斯網絡模型

3 地鐵牽引變電所可靠性分析

3.1 可靠性模型計算

在確定了變電所貝葉斯網絡的拓撲結構、節點先驗概率、條件概率后，對變電所的可靠性模型進行計算，得到該變電所不能對上行接觸網正常供電的概率為0.015 686 644%；若要求變電所的可靠度不低于0.9，為保障變電所的可靠運行，其預防性檢修的時間間隔不宜超過671 h。在動態貝葉斯網絡中設置節點初始概率和轉移概率后，可以得到考慮維修因素時變電所失效率隨時間變化情況，如圖6所示。

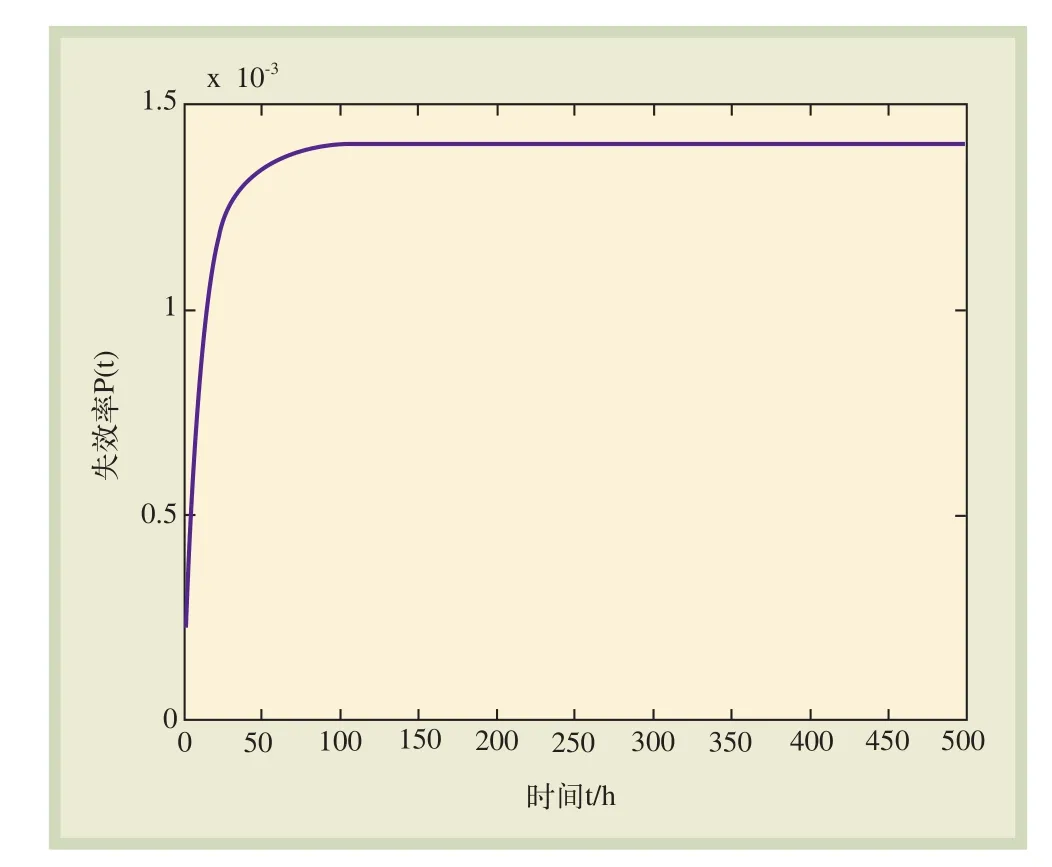
圖6 失效率隨時間的變化曲線

3.2 故障條件下主要節點后驗概率計算

在考慮維修因素時，變電所穩態運行一段時間后可以發現，在運行初期，其失效概率會迅速增長，而隨著時間的推移，在180 h后，失效率達到穩態，其穩態失效率約為0.140 355 05%。同時，利用貝葉斯網絡的反向推理功能，可以分別計算出變電所故障條件下，各元件在靜態貝葉斯網絡和動態貝葉斯網絡中的后驗概率情況，如表6所示。

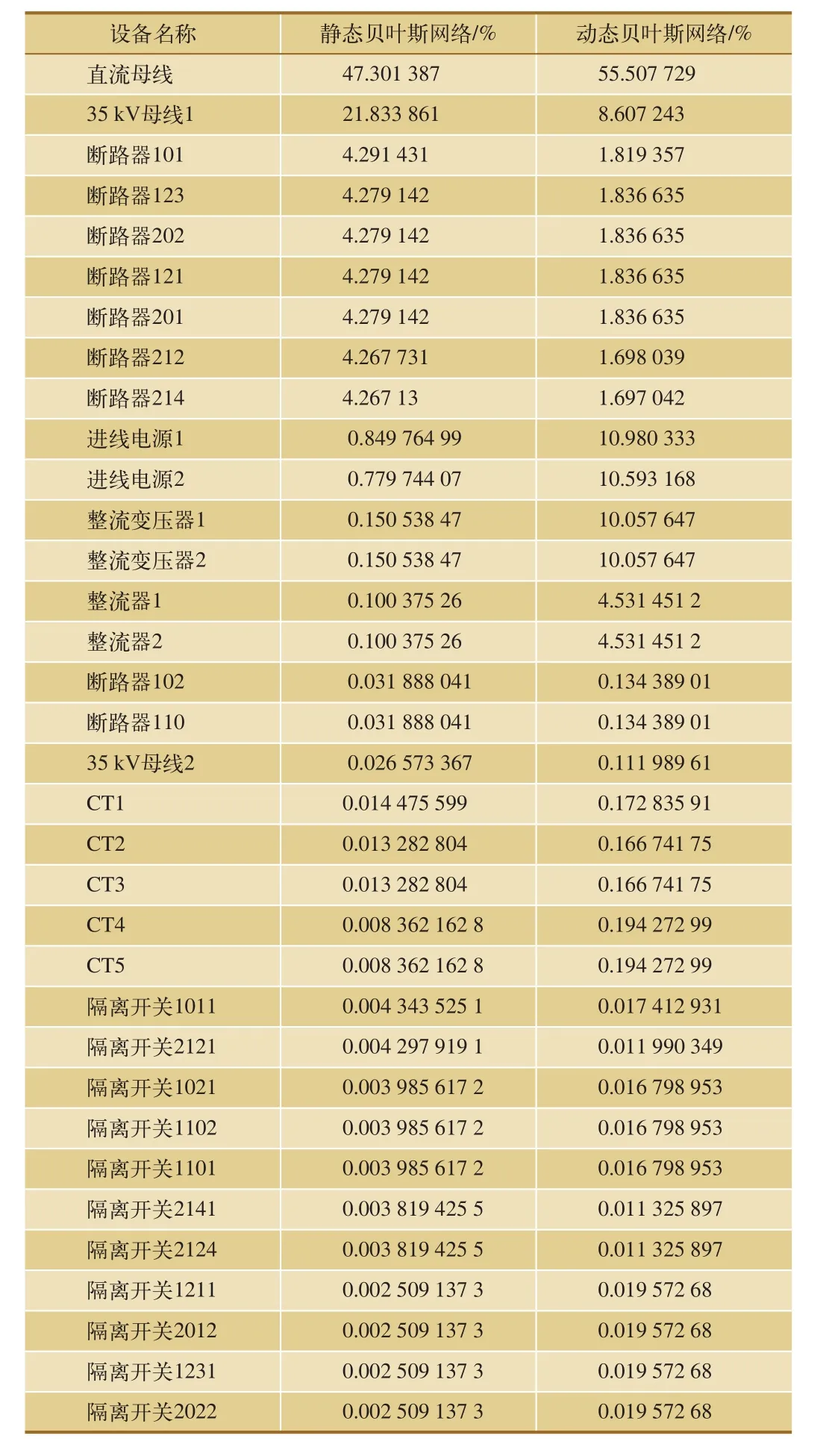
表6 牽引變電所主要節點的后驗概率表

3.3 結果分析

根據表6可知，在靜態貝葉斯網絡中，直流母線、35 kVⅠ段母線對牽引變電所可靠性的影響比較大，后驗概率分別達到了47.30%和21.83%，是變電所可靠性的薄弱環節，上述計算結果與變電所運行中導致變電所失效的直接原因為直流母線或者交流母線斷電的實際情況相符；在考慮到維修因素的動態貝葉斯網絡中，直流母線、35 kV進線電源、整流變壓器等的后驗概率排名比較靠前，說明以上節點是系統穩態后，的薄弱環節，在維護保養過程中需要對以上部件加強維護，以提升各單元的可靠性來提升雙邊供電方式下該供電分區整體的可靠性。

同時，根據表6的對比結果可知，在考慮維修因素后部分節點的后驗概率發生較大變化，其中，主要是整流變壓器、整流器和35 kV進線電源對變電所可靠性的影響大幅提升，說明在考慮維修因素時，設備的維修率會對節點在變電所中的重要度產生影響，如變壓器和整流器等是變電所的關鍵設備，雖然其故障率較低，導致變電所失效的后驗概率較小，但考慮到該設備的修復時間長、修復率低等維修因素時，其對變電所的穩態可靠度影響程度將大幅增大。因此，除了通過降低設備自身的故障率以外，還可以對變電所關鍵設備的維修策略進行優化，使變電所可以長時間維持在較高的可靠度水平上。

4 結束語

本文采用貝葉斯網絡對地鐵牽引變電所進行可靠性分析，通過GeNIE仿真軟件建立了典型變電所基于貝葉斯網絡的可靠性模型，對其發生故障的概率進行計算；利用動態貝葉斯網絡對該變電所在時間維度上展開分析，得到變電所故障概率隨時間變化的曲線；利用貝葉斯網絡的雙向推理功能，計算得到變電所在初始狀態和穩態下各元件的后驗概率排序，找到變電所的薄弱環節。對變電所關鍵節點的識別、維護，以及網絡結構優化具有一定意義。