濕陷性黃土的流變本構模型研究*

歐湘萍 閆志濠 李 塘 朱云升 呂乃芝 郭慧峰 魯 聰

(武漢理工大學交通學院1) 武漢 430063) (浙江省交通規劃設計研究院有限責任公司2) 杭州 310000)(內蒙古高等級公路建設開發有限責任公司3) 呼和浩特 010060)(湖北省交通規劃設計院股份有限公司4) 武漢 430051)

0 引 言

近年來，隨著西部地區高速公路的快速發展，大量黃土隧道建成并投入使用，由濕陷性黃土流變特性所引發的隧道等構造物的長期穩定性問題越來越受到人們的重視[1-2].由于黃土分布的地域性，不同區域的黃土的力學性質與結構特性會有所差異，因此，無論是應力、應變分析還是本構模型[3]的建立都不具有普適性，必須結合當地黃土的實際情況并通過試驗數據分析得出[4-5].文中以蘭州定遠隧道的濕陷性黃土為研究對象，在黃土三軸蠕變試驗的基礎上，對該濕陷性黃土的本構模型進行了研究，以反映濕陷性黃土的流變特性.研究可為解決黃土地區因濕陷性黃土流變而造成的隧道穩定性問題提供借鑒[6].

1 經驗本構模型

經驗模型是能夠反映試樣流變曲線形狀的數學表達式，它直接建立在對試驗數據的分析上，具有簡單明了、參數較少的優點，在工程實踐中應用起來方便快捷.但經驗模型也有其不足之處，譬如缺乏嚴謹理論依據的支持，受試驗條件等因素影響較大，在土體類型和應力狀態改變時，經驗模型的適用性仍有待提高等等.

通過對黃土試樣進行含水率試驗，得到定遠隧道濕陷性黃土的含水率范圍為1.6%～11.7%，由此選取1.6%,5%,11.7%三個含水率下的濕陷性黃土進行經驗本構模型擬合分析.

擬合優度記為R2，常作為反映本構模型擬合效果的表征指標，可以良好的表征模型的適用性.R2取值范圍為0～1，擬合優度越大(越靠近1)，則表示所建模型對試驗曲線的擬合程度越高，越能描述其土樣的實際流變特性.擬合優度的計算公式為

(1)

式中：SSE為殘差平方和;SST為總離差平方和.SSE，SST的計算公式如下.

(2)

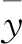
1.1 Singh-Mitchell模型

在現有的經驗模型中，由辛格和米切爾在1968年建立的Singh-Mitchell模型應用較為廣泛，模型數學表達式為[7-8]

(3)

對式(3)進行換元，令B=At1/(1-m),λ=1-m，可將模型公式轉化為

(4)

對式(4) 兩端取自然對數，得

(5)

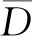
ln (ε-ε0)=λlnt+β

(6)

以1.6%，5%含水率的濕陷性黃土試樣為例，繪出ln (ε-ε0)-lnt散點圖并擬合,見圖1.

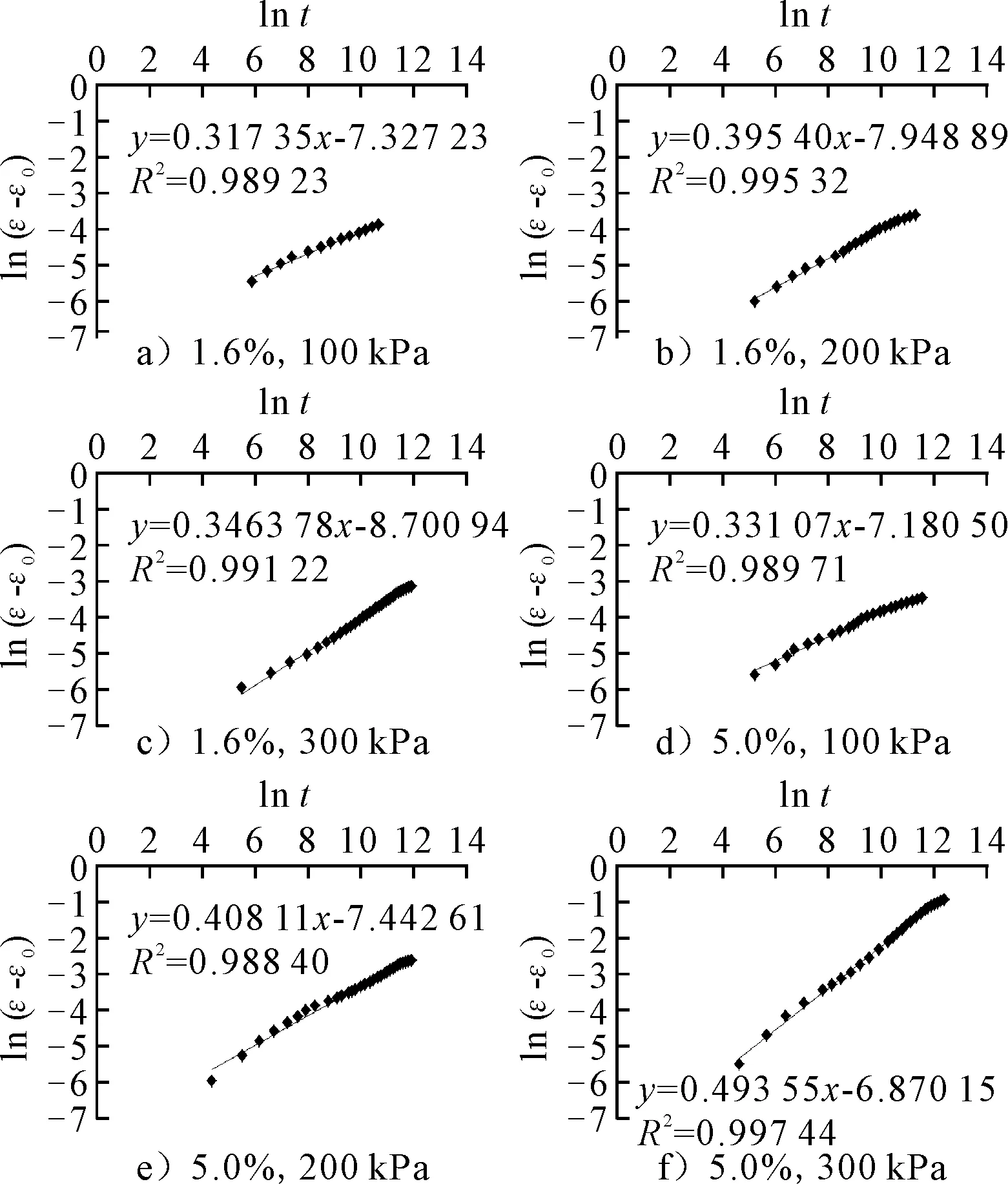
圖1 Singh-Mitchell模型的ln (ε-ε0)-ln t圖

由圖1可知，其應變差-時間雙對數曲線用一次函數擬合時，擬合優度R2均在0.988以上，具有良好的線性關系，由此求得Singh-Mitchell應變-時間本構模型中的參數λ，β取值見表1.

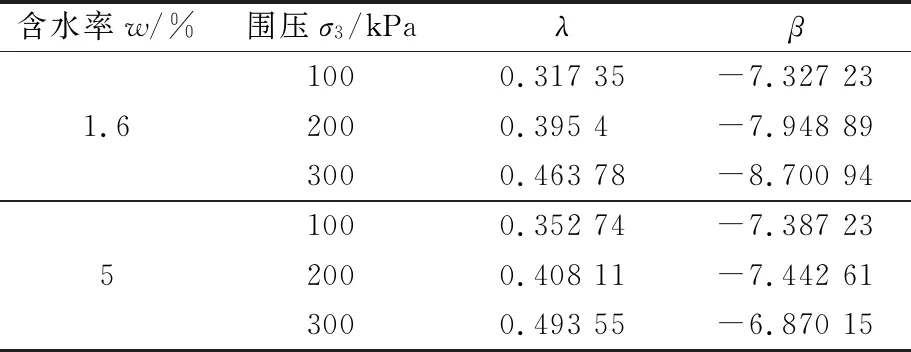
表1 模型參數λ，β取值

獲取參數λ，β后，即可根據以上由式(6)轉化而來的應變-時間式(7)，求出各時間點對應的模型擬合應變，其與實際應變的對比見圖2.

ε=ε0+eβtλ

(7)

圖2 Singh-Mitchell模型擬合圖

計算擬合應變與實際應變間擬合優度R2的值，見表2.

表2 擬合優度R2統計表

由上述相關圖表可知，采用的Singh-Mitchell模型對濕陷性黃土試樣曲線擬合優度值都在0.98以上，線形重合度良好，僅在最末端擬合值稍高于實際應變量.

當時間t與參考時間t1相等時，式(4)可化簡為：

(8)

式(8)兩端取自然對數，求得應力應變關系為

(9)

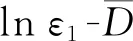
ln (ε-ε0)=aσ3+lnB

ε-ε0=Beaσ3

(10)

取參考時間t1為1 h，繪出1.6%，5%兩種含水率下濕陷性黃土試樣的ln (ε-ε0)-σ3散點圖，擬合情況見圖3.

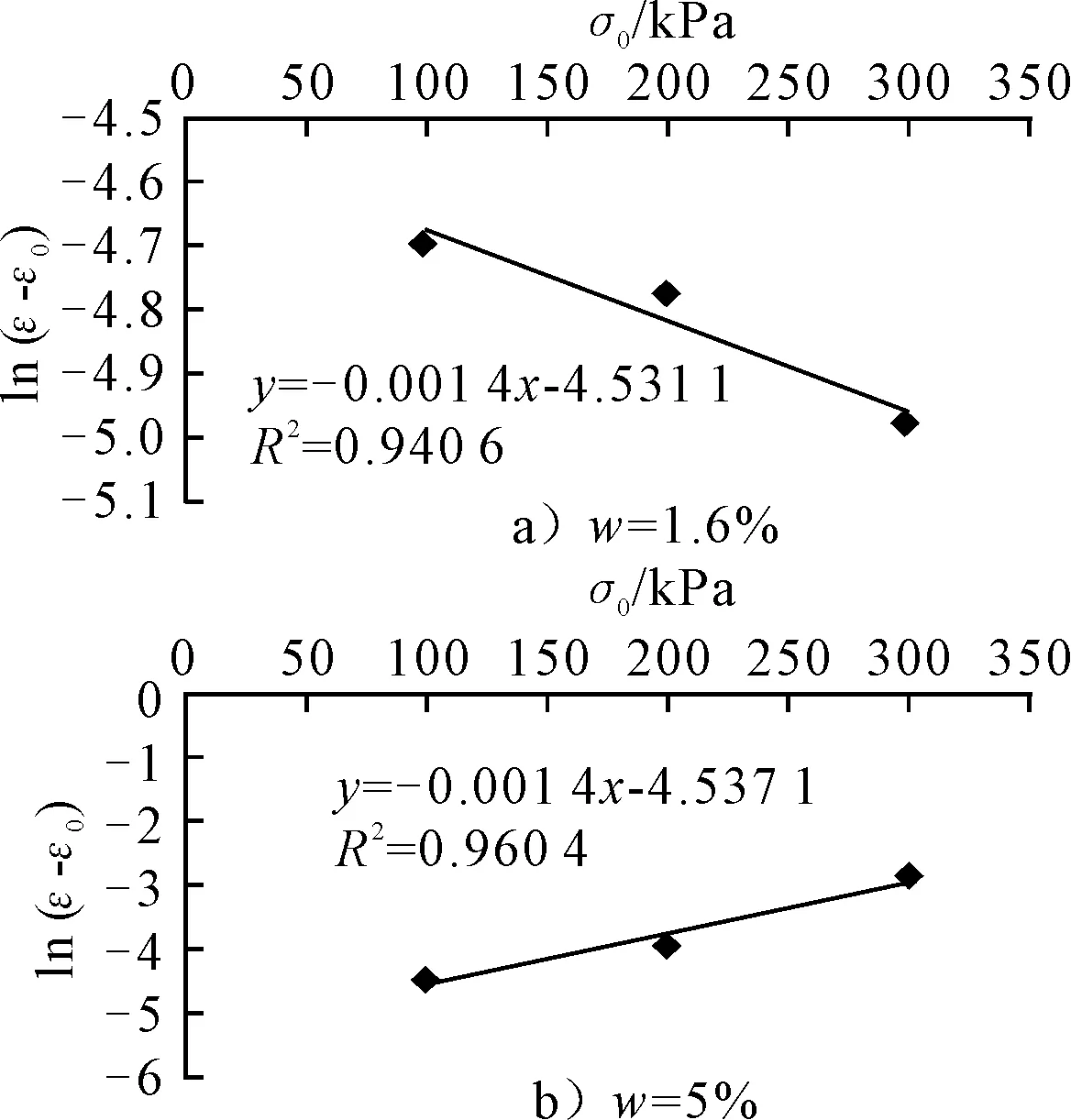
圖3 ln(ε-ε0)-σ3關系圖

由圖3中的擬合情況及擬合優度R2取值中可知，當試驗時間t=t1=1 h=3 600 s時，本試驗所用土樣的應變差對數值與試驗所用圍壓σ3有較好的對應關系，參數a，B值計算見表3.

表3 參數a，B計算值表

因此，1.6%，5%兩種含水率下的濕陷性黃土試樣在t=3 600 s時所對應的Singh-Mitchell擬合方程為

1.6%含水率土樣：ε-ε0=0.010 8e-0.001 4σ3

5%含水率土樣：ε-ε0=0.004 6e0.008 1σ3

(11)

上述所討論的Singh-Mitchell模型擬合精度相對較高，且模型參數可與圍壓建立關聯，具有一定的物理意義，但也存在著適用范圍不廣的問題.經過進一步計算發現，對本試驗中11.7%含水率試樣的試驗曲線用Singh-Mitchell模型擬合時，其擬合優度較低.Singh-Mitchell經驗本構模型無法完整描述本試驗中1.6%，5%，11.7%三種含水率黃土試樣的應變-時間關系，原因在于所取黃土在不同含水率時的應變-時間曲線會表現出較大差別：較低含水率(1.6%與5%)下，試樣蠕變曲線的應變率趨向于均勻減小；而對11.7%的較高含水率試樣，由于其結構強度偏低導致蠕變總量本就普遍高于較低含水率試樣，因此可以看出Singh-Mitchell經驗模型適用于擬合后期仍有較可觀應變的末端傾斜曲線.

1.2 對數經驗本構模型

為了建立能夠同時反應本試驗中較低含水率(1.6%，5%)與較高含水率(11.7%)的濕陷性黃土試樣流變特性的經驗本構模型，在分析得知模型擬合效果與流變后期曲線應變率有關后，決定以最常用的對數模型ε=A+Blnt為藍本，增加一個可自由控制曲線末端斜率且與時間相關的Ct因子，所得模型為

ε=A+Blnt+Ct

(12)

本對數模型中有A，B，C三個參數，選擇采用OrignPro 8.0分析軟件進行擬合，得到的對數經驗本構模型擬合結果見圖4.

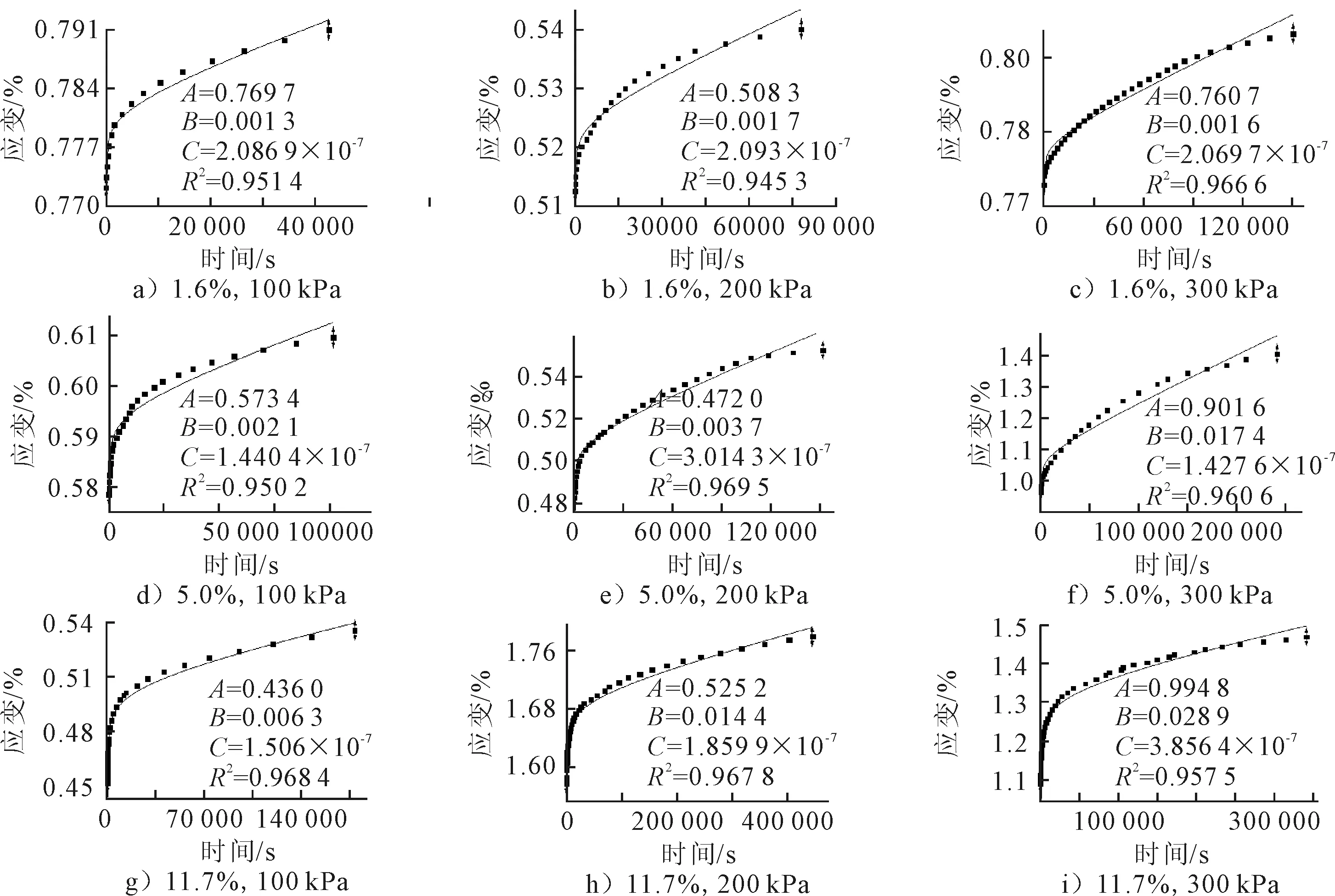
圖4 對數經驗模型擬合圖

文中采用的對數經驗模型對本試驗中1.6%，5%，11.7%三種含水率試樣的應變-時間曲線都能達到較高的擬合程度，且擬合優度處于0.94～0.97范圍內，擬合效果比較穩定.由于加入了與時間相關的Ct單項式，末端的計算應變值依舊普遍略大于試驗應變且仍保持有穩定的增加趨勢，這與實際流變試驗中試樣應變最終趨于穩定的現象有所出入.

對數經驗模型參數與擬合優度R2見表4.

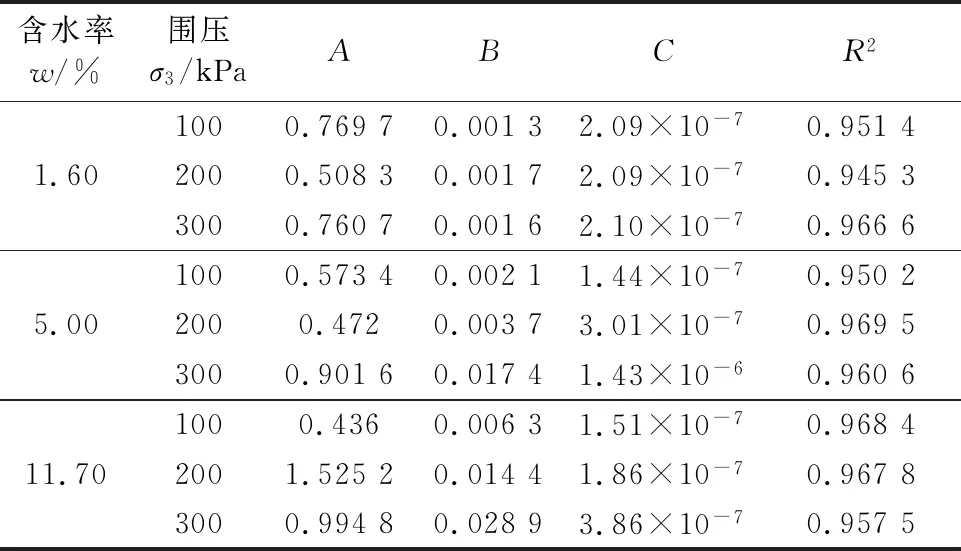
表4 對數經驗模型參數及擬合優度R2表

由表4可知，參數A取值與試樣初始應變ε0大小相近，變化規律也與之相同：較低圍壓(100 kPa)下A隨含水率的增大而變小，較高圍壓(300 kPa)下則相反，可知本模型中A值代表的含義等同于初始應變.參數B作為與對數時間相乘的因子，在100，200和300 kPa三種圍壓下都隨含水率的增大而增大；而表征曲線末端第二流變階段常應變速率的參數C則與圍壓(偏應力)的變化有明顯關聯，對同一含水率試樣，流變趨向于穩定前的應變率隨偏應力的增大而增大，見圖5.

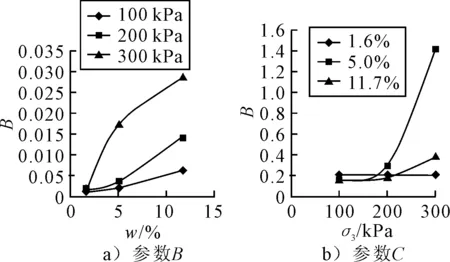
圖5 參數B，C變化規律

2 Burgers元件本構模型

元件模型法是將Hooke彈性體、Newton黏壺及St. Venant塑性體等分別反映彈性、黏滯性、塑性等不同力學特性的元件按照土體實際性質組合成力學模型，然后根據試驗數據求出組合模型各項參數的方法.

首先結合卸載回彈階段的應變情況，可知所需元件模型應至少包含造成初始應變的串聯彈性體與一個可產生彈性后效的開爾文體，此時即構成三單元的廣義開爾文模型，但該模型的曲線末端趨于平緩，僅可反映第一階段蠕變趨于穩定的情況.從建立對數模型的經驗中可知，文中所得試驗曲線的末端普遍較為傾斜，應處于具有常應變速率的第二蠕變階段，與增加可自由控制曲線末端斜率且與時間相關的Ct項類似，因此，決定在廣義開爾文模型的基礎上，增加一個反映常應變速率的串聯粘壺元件，最終形成了反映土樣粘彈性的四參數Burgers(伯格斯)模型，其結構見圖6.

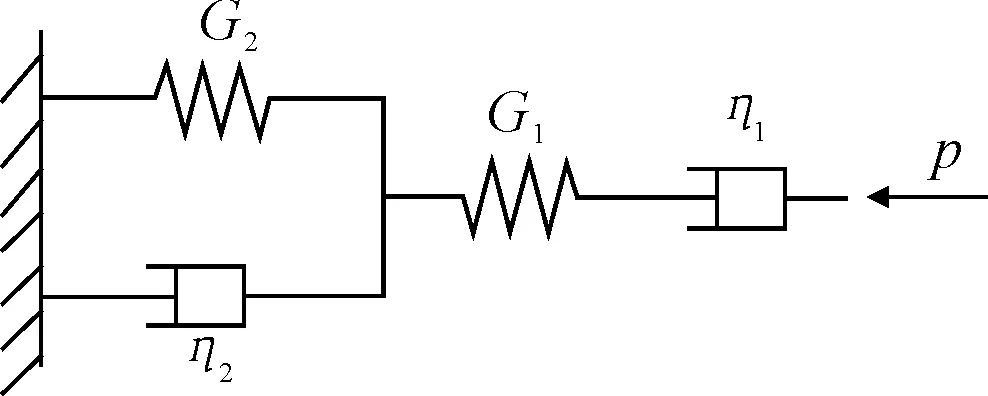
圖6 Burgers模型結構

由圖6可知，所選用的Burgers元件模型由四個單元構成：虎克彈簧G1與牛頓黏壺η1串聯形成Maxwell(麥克斯韋)模型，彈性體G2和黏壺η2并聯構成Kelvin(開爾文)模型，最后再將Maxwell體與Kelvin體串聯，最終形成Burgers模型.

本文中的濕陷性黃土流變試驗是在三向應力狀態下進行，對Burgers模型中的彈性體變形情況應采用剪切模量G與體積模量K來表示，模型變形計算公式為

(13)

式中：σⅠ，σⅡ與流變的三向應力大小有關，其公式為

σⅠ=σ1-σ3

σⅡ=σ1+2σ3

(14)

式中：剪切模量G體現的是三向加壓狀態下由于偏應力引起虎克彈性體形狀改變的性質，體積模量K則體現了在三向等壓狀態下的體變特性，其方程為

(15)

(16)

式中：E為彈性模量；μ為土體泊松比，本次試驗所取濕陷性黃土泊松比參考值μ為0.44，再通過式(15)～(16)可將Burgers模型中需擬合的未知量轉化為E1，E2，η1，η2四個參數，它們分別代表著本構關系中兩個彈性體的彈性模量與兩個粘壺的粘滯系數.

2.1 模型參數計算

對Maxwell體中串聯彈性體參數E1，令試驗時間t=0，綜合式(13)～(16)可得

式中：t=0時的初始應變ε0可從試驗中獲得，其余參數σ1，σ3及μ值均已知，則可求出E1.

對串聯粘壺系數η1，從伯格斯本構模型式(13)可知，σⅠ/3η1即為流變曲線斜率.對所得應變-時間曲線，當t較大時，將曲線末端視為直線并通過線性回歸求出斜率值k，則可通過式η1=σⅠ/3k計算出η1.

求取Kelvin體中的模型參數E2，η2時，需在Burgers本構方程(13)中令t趨于無窮大，則有

(18)

用式(18)減去式(13)可得q值：

(19)

q值為蠕變末端漸近線與實際應變之差，對式(19)兩端取對數，可得

(20)

繪出lnq-t關系散點圖，按照線性回歸對其添加趨勢線，求得擬合直線的截距和斜率，再結合式(14)～(15)分別求出E2,η2的數值.

2.2 模型擬合結果分析

按照2.1的三個步驟可計算出不同含水率(1.6%,5%,11.7%)和不同圍壓(100,200和300 kPa)下濕陷性黃土試樣的伯格斯參數值，將其代入伯格斯模型式(13)中，可得各試驗條件下的應變-時間函數，從而求出各時間點的擬合應變與實際應變值，見圖7.

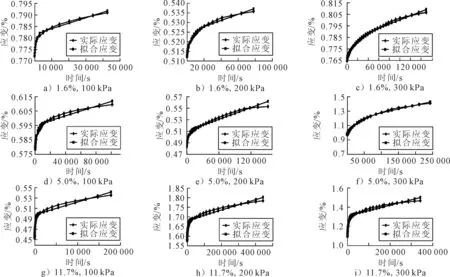
圖7 Burgers元件模型擬合圖

由圖7可知，由于Burgers模型的力學特性決定了擬合曲線末端是具有常應變速率的的第二流變階段，而實際試驗中應變時間曲線后期則是趨于平緩，應變速率逐漸減小,因此,擬合曲線的尾部均有稍高于實際應變量的現象.但從整體擬合情況上看，伯格斯模型擬合應變與實際應變間的擬合精度R2值都大于0.96，見表5.可以較好地描述本試驗中所有濕陷性黃土試樣的流變性質.

3 結 論

1) 在兩種經驗本構模型中，Singh-Mitchell模型對兩種含水率下(1.6%,5%)的濕陷性黃土流變試驗曲線的擬合優度R2值均在0.98以上，在兩種經驗本構模型中擬合優度較高，但適用范圍有限，無法反映試驗中較高含水率下(11.7%)試樣的流變特性；經過修改的對數經驗模型，其擬合優度R2在兩種經驗模型中處于中等水平，但可適用于本試驗中三種含水率下(1.6%,5%,11.7%)的濕陷性黃土試樣全部應變曲線，是擬合效果更好的經驗本構模型.

2) Burgers元件模型對濕陷性黃土流變試驗曲線的擬合優度R2高于對數經驗本構模型，也可適用于不同含水率(1.6%,5%,11.7%)與不同圍壓(100,200和300 kPa)下的濕陷性黃土試樣的流變特性分析，且各元件參數意義較為明確.因此，在對定遠隧道進行穩定性分析與變形預測中，Burgers元件模型比對數經驗本構模型更為合適.

表5 Burgers元件模型參數表