考慮目的地選擇的交通流分配雙層規劃模型及算法*

何勝學

(上海理工大學管理學院 上海 200093)

0 引 言

選擇出行目的地和具體出行路線是交通出行的兩個基本決策，也是進行交通網絡系統運行效率評價和交通系統規劃的重要組成部分.傳統的交通規劃四步驟法將上述兩個決策按序分別考慮，忽視了兩個決策間存在的相互影響.因此有研究者針對上述問題試圖將兩個決策問題整合為一個單層優化模型，但是在嘗試構建這些單層組合模型過程中出現的特殊參數標定與不合理概念使得這些模型很難應用于實際.針對上述問題，本文嘗試建立相應的雙層規劃模型來合理反映兩個決策的特征與差異，并設計有效算法求解上述雙層規劃模型.

Wardrop提出了出行路徑選擇兩原則，即Wardrop第一原則(用戶均衡)和Wardrop第二原則(系統最優).Beckman給出了用戶均衡交通流分配優化模型，即有名的Beckman變換.Leblanc首次給出了求解用戶均衡模型的實用有效Frank-Wolfe算法.近年來研究者開始應用投影動態理論對動態和擬動態的交通流分配問題進行建模分析[1-4].針對路段流量一般受限于路段通行能力的情況，研究者也提出了有邊約束的交通流分配變分不等式模型[5-6].為了反映路段行程時間函數具有的兩階段特征，最近研究者開始利用非凸規劃理論研究交通流的分配和網絡演化問題[7-8].

交通流分配中的組合網絡模型也是研究者關注的重點.大致可分為：運量分布與交通分配組合模型、方式分擔與交通分配組合模型、運量分布/方式分擔/交通分配組合模型[9].本文關注的運量分布與交通分配組合模型又可分為：單運量分布約束組合模型和雙運量分布約束組合模型.現有運量分布約束組合模型多為單層模型.運量分布約束組合模型中均需設定目的地吸引力測度指標Ms，?s∈D[10].令O和D分別為起點和終點集合.令μrs為起點r∈O與終點s∈D間最短的可行路徑行程時間.運量分布約束組合模型通常依據μrs-Ms大小決策起訖點對間交通量.Ms的量綱需要與μrs一致，在實踐中通常很難給出符合要求的合理值.為了方便后續求解，考慮終點需求函數的單運量分布約束組合模型和常見的雙運量分布約束組合模型一般會基于熵最大化理論在目標函數中加入對應項.而該加入項的系數需要利用歷史的起訖點對間完整交通需求量加以標定，而該信息在現實應用時一般很難取得的.考慮到上述問題，本文通過建立雙層規劃模型，免去對熵最大化理論加入項系數進行標定的工作，同時放松了對目的地吸引力測度指標Ms量綱的限制.在建立的新模型中，終點s作為出行目的地對出行者的吸引力系數標定將更加方便和符合實際.

本文主要的貢獻包括：①建立了考慮目的地選擇的交通流分配雙層規劃模型.上層模型拓展了目的地選擇概念，可以適用于各種已有的目的地選擇理論，如重力模型和熵最大化模型.②設計了求解上述雙層規劃的有效算法.通過將下層路徑選擇模型抽象為一個映射，并利用經典Frank-Wolfe法對其進行求解，從而可以更有效地對上層目的地選擇模型設計求解方法.將針對下層模型的Frank-Wolfe法嵌入為上層模型設計的可行下降方向法中，最終實現雙層規劃模型的求解.

1 模型構建

1.1 參變量介紹

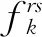
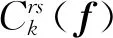
1.2 目的地選擇假設

經典的網絡交通流分配模型一般假設起訖點對間的交通需求qrs給定.而實際中，交通規劃者往往通過交通出行調查只知道任意起點總的交通需求量qr.因此需要對出行者的目的地進行選擇，使其滿足如下的起點基本流量守恒條件.

(1)

一般而言出行者對出行目的地的選取不僅需要考慮出行的行程時間長短，也許考慮備選目的地的吸引力大小.這里的吸引力主要指備選目的地滿足出行者出行目的的可能性.例如，對于出行者購物需求，如果目的地是一個商業購物中心，則具有較強的吸引力.用吸引力系數As的值表示目的地的吸引力大小.在后續分析中，假設As的值給定.

下面給出兩種情況確定目的地選擇比例wrs的方法.第一種情況下，假設wrs滿足

(2)

式中：m為一給定正整數，一般取值1或2.當m等于2時，式(2)與出行分布中的重力模型相一致，即由確定起點出發的出行者中選擇某終點為目的地的數量與該起訖點對間的行程時間平方成反比.

第二種情形源于熵最大化理論，假設wrs滿足

wrs=Asexp(-μrs)/∑d∈D[Adexp(-μrd)] (3)

至于實際中應用哪種假設則需要根據具體情況進行估計選擇.兩種情況下，∑s∈Dwrs=1均成立.

如果有了目的地選擇比例，起訖點對間的期望交通需求量為

(4)

如果μ為由所有μrs構成的列向量，可將wrs視為μ的函數，即wrs=wrs(μ).

1.3 下層路徑選擇行為模型

針對出行者的擇路行為，對應的用戶均衡模型(user equilibrium model，UEM)為

(5)

(6)

(7)

(8)

與經典用戶均衡模型的唯一差別在于上述模型中起訖點對間的交通需求量是待定的.式(6)為連接指定起訖點對的可行路段上的路徑交通流量之和等于該起訖點對間的交通需求量.式(7)為路徑流量的非負約束.式(8)為一個隱含約束條件，表明指定路段流量等于所有途經該路段的路徑流量之和.式(5)可理解為所有路段的流量逐步累計過程中單位流量行程時間的加和.

(9)

式中：上標“*”為相關量對應模型的最優解.

1.4 上層目的地選擇模型

給定起訖點對間的交通需求模式q，由下層優化模型可以確定一個唯一的μ.上述關系可以抽象為映射μ=Ψ(q)或μrs=Ψrs(q)，?rs.因此，wrs=wrs(μ)=wrs(Ψ(q))成立.

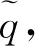
(10)

式中：q的可行集合定義為Q≡{q|qrs≥0,?rs∈W;∑s∈Dqrs=qr,?r}.

2 求解算法

下層模型(即抽象映射μ=Ψ(q)) 可利用Frank-Wolfe法進行求解，具體步驟為

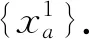
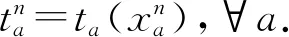
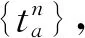
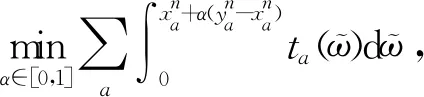
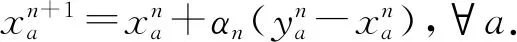
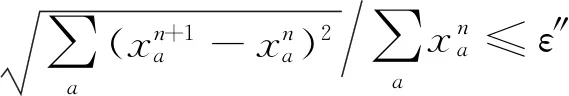
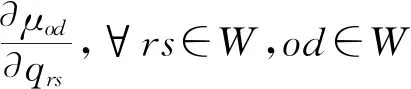
下面我們為式(10)設計一個可行下降方向法.由模型(10)的目標函數，可得

(11)

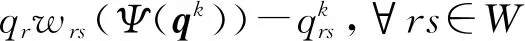
利用式(11)給出的dk可對q進行如下更新.

qk+1=qk+αkdk

(12)

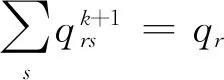
具體步長αk的確定可以利用一維搜索算法實現.鑒于實現的復雜性，應當盡量減少調用下層求解算法的次數，因此可采用一些啟發式一維搜索算法，如Armijo法.Armijo法中的步長αk=βmks，mk是從小到大滿足下式的第一個非負整數：

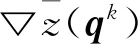
以式(2)作為目的地選擇比例的計算式，求解雙層規劃的具體步驟為

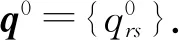
步驟2計算新的最短路行程時間.調用求解下層規劃UEM的算法，計算得到μk=Ψ(qk).

步驟3方向搜索 按照式(11)，計算可行下降方向dk.

步驟4步長計算 利用Armijo法，依據式(13)計算得到αk.

步驟5交通需求模式更新.令qk+1=qk+αkdk.

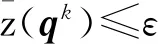
步驟6中的ε和ε′均為事先給定的較小正數，作為收斂指標.注意算法中目的地選擇比例wrs的計算方法應保持一致，可以選擇式(2)～(3)，也可以選擇其他可能的形式.

3 算例分析

本節利用Nguyen和Dupius路網[11]來對本文提出的模型和算法加以驗證.該路網包含13個節點，其中節點1和2為起點，3和4為終點.相關節點和路段的標號見圖1.算法的終止指標設定為ε″=0.001、ε=0.05和ε′=0.05.上層模型算法中Armijo步長搜索的參數設定為σ=0.6、β=0.5和s=0.5.以式(2)中參數m為2時的重力模型來確定目的地選擇比例.

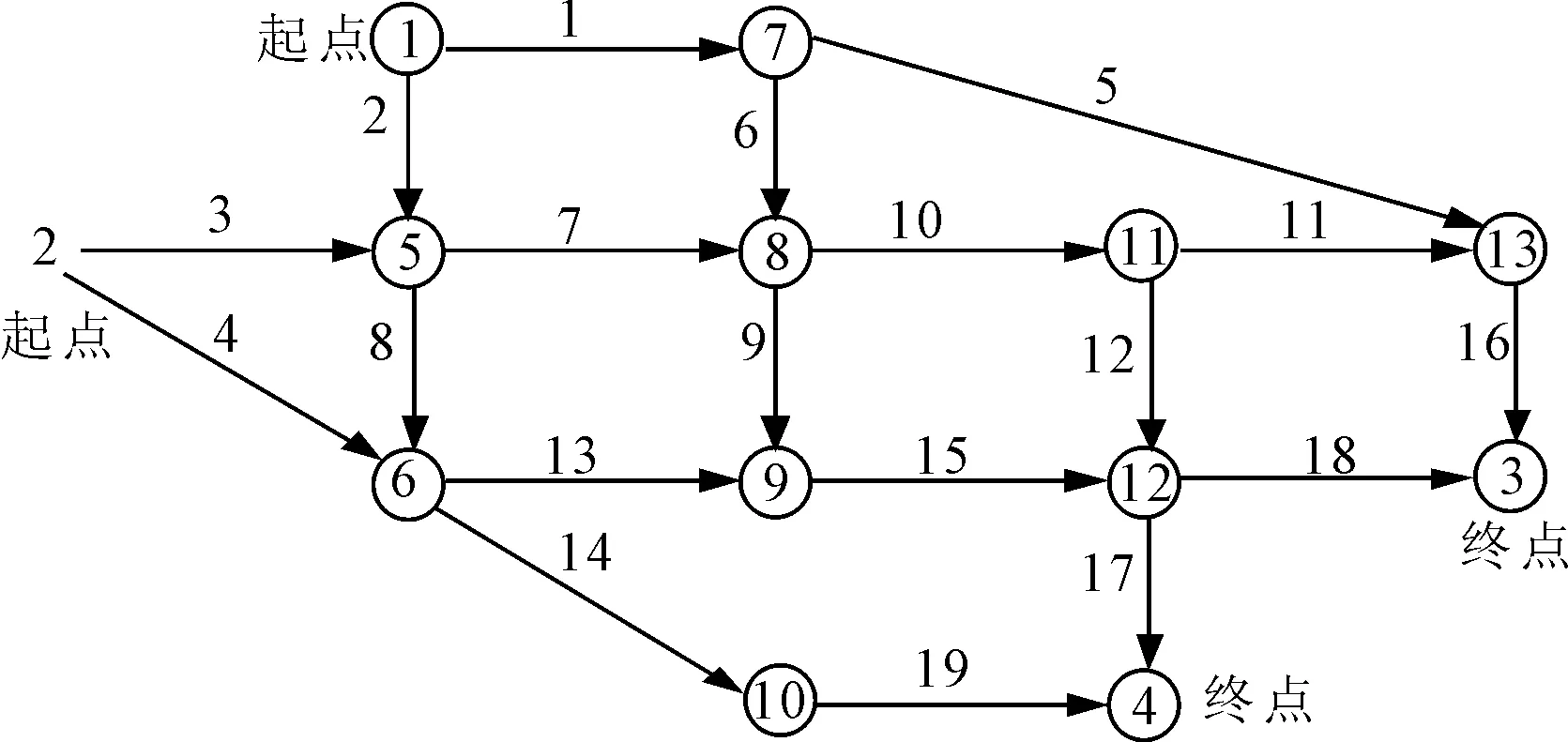
圖1 13個節點的Nguyen和Dupius路網

考慮兩個不同的情景進行計算分析.情景1設定起點①和②的交通需求量分別為1 800和1 300，而終點③和④的吸引力系數分別為100和210.情景2設定起點①和②的交通需求量分別為1 800和2 300，而終點3和4的吸引力系數分別為200和120.

利用Java程序語言實現上節的算法，并在NetBeans IDE 8.0.2環境下執行.路段均衡流量的計算結果總結見表1；最終的交通需求分布結果見表2；計算過程中上層目標函數的變化記錄見表3.兩種情境下上層算法均執行七次后收斂，雙層模型整體求解的運行時間均小于1 ms(即計算機顯示執行時間為0，小于其可給出的最小時間單位1 ms).利用節點流量守恒條件可判定計算結果的合理性.

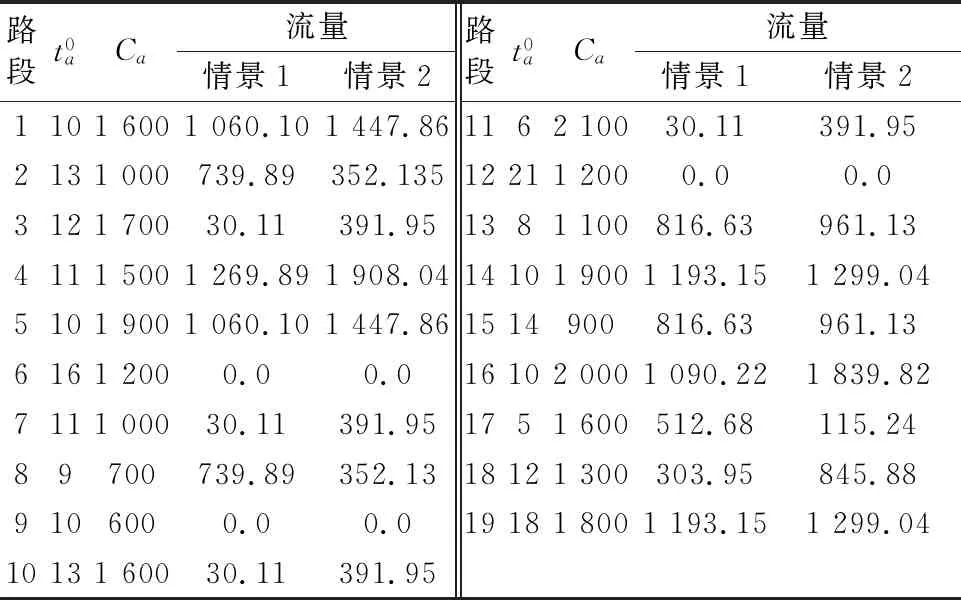
表1 路段行程時間函數的參數和均衡流量

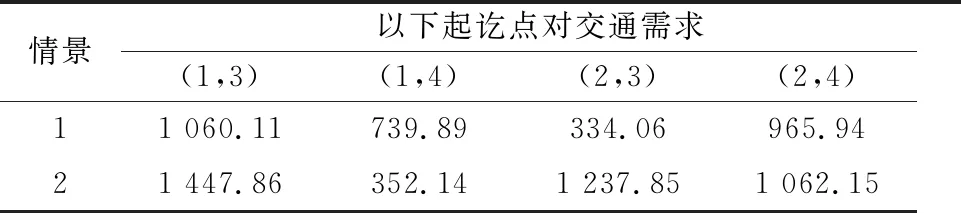
表2 交通需求分布結果

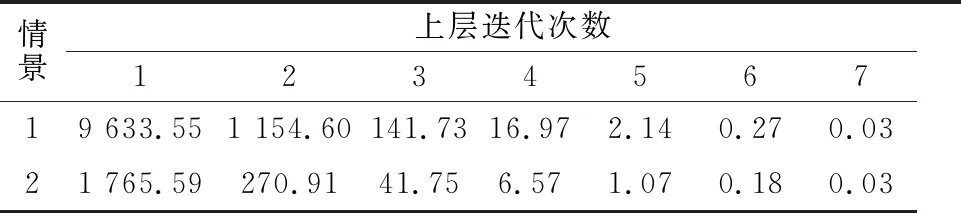
表3 上層目標函數變化情況

4 結 束 語

綜合考慮出行目的地選取和路線選取兩種決策，可以有效提高交通系統規劃和系統運行評價的準確性和可靠性.本文通過設計整合兩種決策的雙層規劃模型，不僅拓展了現有理論處理目的地選擇模型的靈活性，也降低了現有模型應用時面臨的參數標定工作.本文設計的內嵌經典用戶均衡模型的Frank-Wolfe法的可行下降算法可以實現對本文雙層規劃模型的高效求解，因此其實際應用前景良好.