突發事件下城市交通影響范圍研究*

馬庚華 鄭長江 付文進 楊淑茜

(河海大學港口海岸與近海工程學院1) 南京 210098) (河海大學土木與交通學院2) 南京 210098)

0 引 言

當前各類突發事件在大城市發生的頻率越來越高，對城市居民的生命安全和社會的穩定發展形成很大的威脅，對突發事件的相關理論與應急處理措施進行研究顯得十分重要[1].城市交通突發事件影響范圍大、破壞性強，已嚴重影響交通網絡的正常運行，造成很大的資源浪費，為了盡可能的縮小突發事件的影響及實施正確的應急疏散措施，應對城市交通突發事件影響范圍進行研究.

通過科學合理地預測城市道路突發事件影響范圍，為制定切實、有效的交通應急疏散方案提供基礎，避免突發事件所引發的交通堵塞不斷惡化[2]，同時快速清除突發事件造成的惡劣影響，使城市交通穩定健康運行.

1 基于時空消耗的道路擁堵影響分析

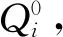
1) 時空容量損耗時間T(h)

(1)

2) 突發事件延誤時間內時空容量損耗計算 假設在車輛排隊過程中，每輛車占據路面長度為ls(m)，在突發事件完全清除之前，事發路段產生的時空容量損耗為Cs1，則有

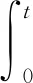
(2)

3) 突發事件消散時間內時空容量損耗計算 在突發事件處理后，交通逐漸恢復正常，但在此過程中，仍會引發一定的時空損耗Cs2，則有

(3)

4) 時空容量損耗計算 其實，當突發事件發生后，事故車輛本身會占用部分道路資源，引發一定時空容量損耗，但其損耗太小，可直接忽略[4].所以時空容量損耗為

(4)

根據對式(4)進一步研究分析，可以得知道路時空容量損耗與上游到達流量、瓶頸路段通行能力、事件持續時間等因素關系密切，總的容量損耗是基于這些參數的函數.

2 基于Van Aerde模型的突發事件影響范圍預測

突發事件影響范圍主要受瓶頸段通行能力、上游到達交通流與事件持續時間影響[5].選擇合適的交通流模型可以較為準確地描述突發事件下擁堵擴散的過程，并分析出突發事件交通影響范圍[6].在交通流模型中Van Aerde模型使用頻率較高，該模型主要通過數學方法對以往數據進行模擬以及數據分析，然后用直觀的圖形關系表現出交通流三要素之間的內在數學聯系.通常突發事件發生后，事發路段處于擁擠環境，車輛行駛速度緩慢，但此時路段的車流密度卻非常高，該模型在擁擠路段下交通流參數之間的關系基本符合二次函數，于是只要獲知其中某一個參數，就可以得到整個交通流參數之間的關系，相關變量容易測取，具有很強的適用性.因此本文選擇VanAerde模型作為基礎模型來建立城市道路突發事件影響范圍預測模型.主要針對城市快速路發生突發事件后[7]，對其影響范圍進行確定.

突發事件下車流波波速為

(5)

進一步整理可得：

(6)

式中：

(7)

如果突發事件發生后，導致車道完全封閉，則有

(8)

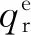
若求取的Vw值為負，表示交通波沿著相反方向往事發點上游傳播，在下文計算影響范圍時，均取其絕對值進行計算.

對波速公式進行分析可以得知，不同交通運行情況下的車流波波速是不一樣的[8]，這代表該模型與實際交通狀況相符合.并且該模型參數主要受事發點通行能力、上游交通量有關，與前文分析相符合.

設集結波波速為vgw，消散波波速為vdw，突發事件持續時間為td，在時刻tjd，集結波與消散波在事發點上游相遇，擁堵持續時間為tjdm.

假設在突發事件完全清理之前，瓶頸路段的斷面通行能力保持不變，上游路段交通量沒有顯著變化，那么事發點左右兩側密度沒有明顯變化[9]，此時在時間tjd內僅會有一道集結波和消散波.

由此可以計算突發事件后路段上游不斷積累的排隊長度：

1) 在突發事件延誤時間內上游車輛最大排隊長度為

L1=vgw·td=Lmq

(9)

2) 突發事件消散時間內事發路段排隊長度為

L2=vgw·tjd=Lmax

(10)

還存在另外一種情況，由于突發事件本身的特性，它的演化狀況無法得知[10]，所以極有可能在突發事件的作用下，引起瓶頸路段的通過車輛量發生變化，或者采取相關應急措施后，上游車流量變小，此時就會導致兩個波速不斷發生變化：

1) 在突發事件延誤時間內上游車輛最大排隊長度為

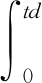
(11)

2) 突發事件消散時間內事發路段排隊長度為

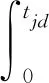
(12)

通過以上分析可知，對于不同情況下的突發事件，應該根據事件處于的時間階段和具體情況選擇正確的排隊長度計算方式，并且，只要知道模型中的波速大小和事件持續時間即可預測出事件影響范圍.

3 仿真分析

以南京市內環西線快速路路網數據為基礎，利用VISSIM軟件對突發事件下的擁堵擴散進行仿真，見圖1.通過對內環西線歷史流量數據的分析，設置仿真路網快速路參數道路總長1 km，車道數為單向3車道，仿真總時長為30 min，上游車輛到達量設置為1 500 pcu/h，自由流車速為70 km/h，假設突發事件發生在路段800 m處，在道路前方設置障礙物模擬突發事件，導致最左側一條車道阻塞，車輛需繞行通過，通過仿真獲取路段因突發事件導致的最大排隊長度.

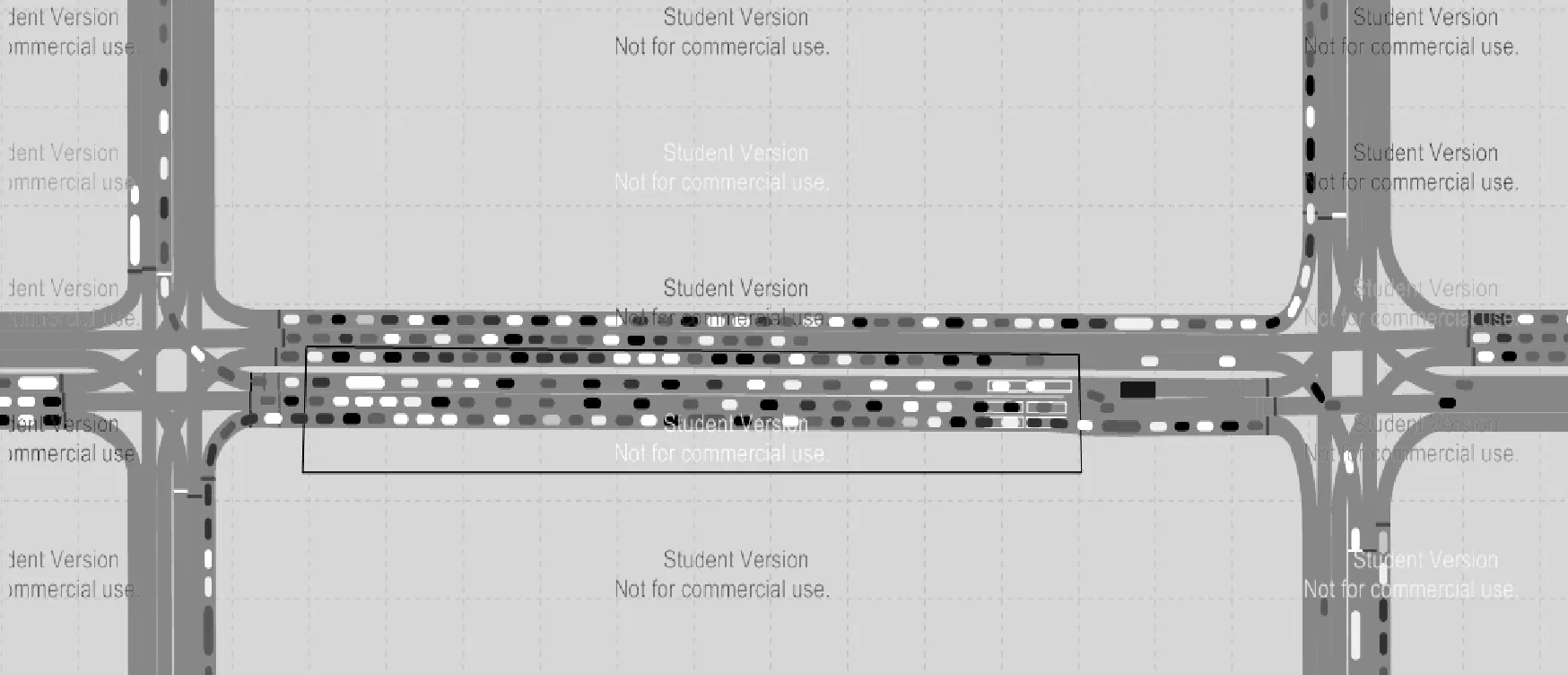
圖1 VISSIM仿真效果圖

在仿真路網快速路參數道路總長1 km，車道數為單向3車道的基礎上，改變事件持續時間、占用車道數、上有到達交通量等變量，并通過VISSIM軟件進行分析，得到不同突發情況下的排隊長度見表1.通過表中數據可以得到時間持續時間、占用車道數與上游到達交通量均會顯著影響排隊長度，并呈現出一定的正相關關系.

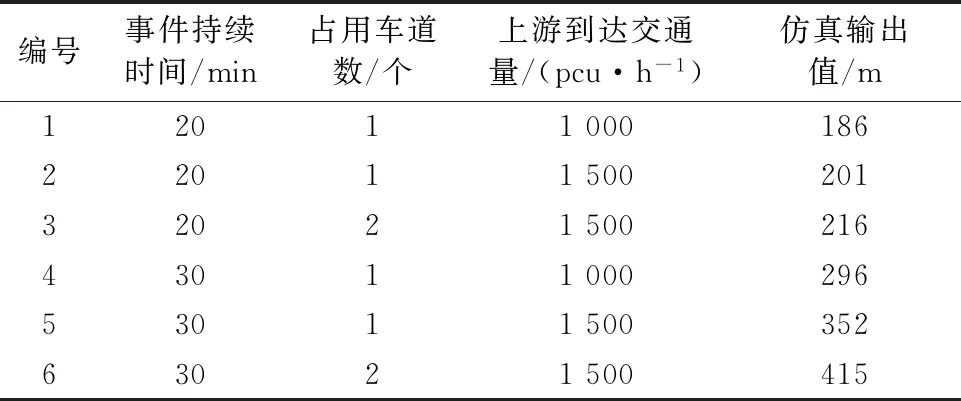
表1 突發事件下的排隊長度VISSIM 輸出結果

首先,根據內環西線快速路歷史車流量數據和區段內的車輛行駛速度，描述交通流各參數之間的內在聯系，繪制內環西線快速路06:00—18:00的12 h流量時變曲線.根據相關VanAerde模型標定成果，可知內環西線快速路的交通流特征參數值見表2.

表2 基于VanAerde模型的內環西線交通流特征參數

根據表中標定的模型特征參數vf,vm,kj,Qm的值，求取中間變量的值.

(13)

在獲得中間變量的值以后，計算0～20 km/h的速度區間內0.2 km/h速度間隔下的密度和流量,并將兩者關系繪制成圖，見圖2.

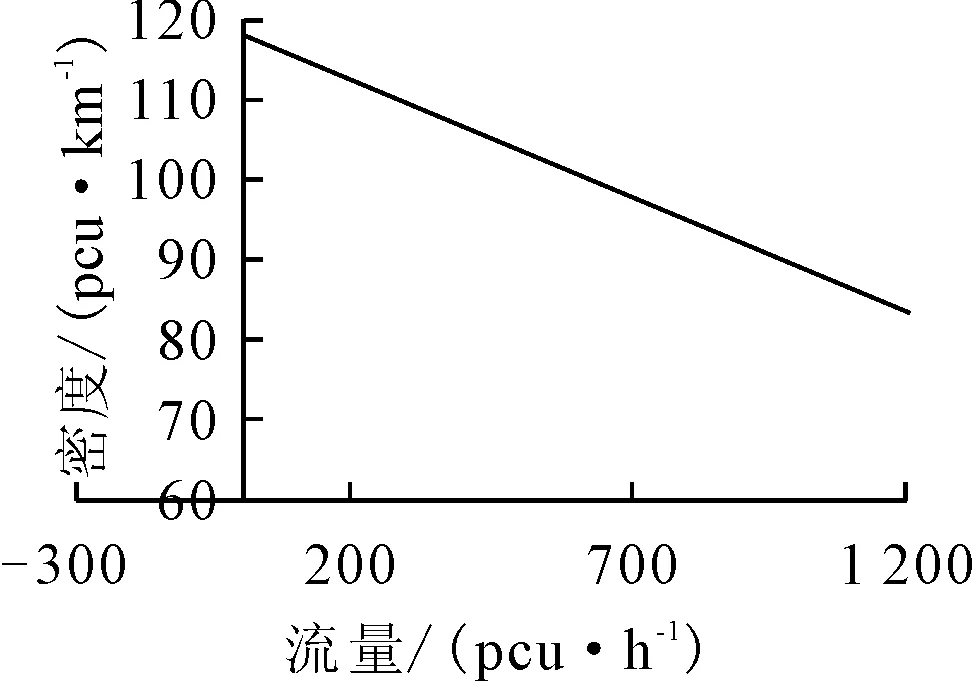
圖2 基于VanAerde模型的擁擠流下密度-流量曲線

a取值為-1.3×10-6，b為取值為0.028 36,c取值為117.9.即該路段擁堵狀態下的密度-流量關系式為

k=-1.3×10-6·q2-0.028 36·q+117.9

(14)

不同突發事件情況下的仿真輸出值與模型計算值結果見表3.

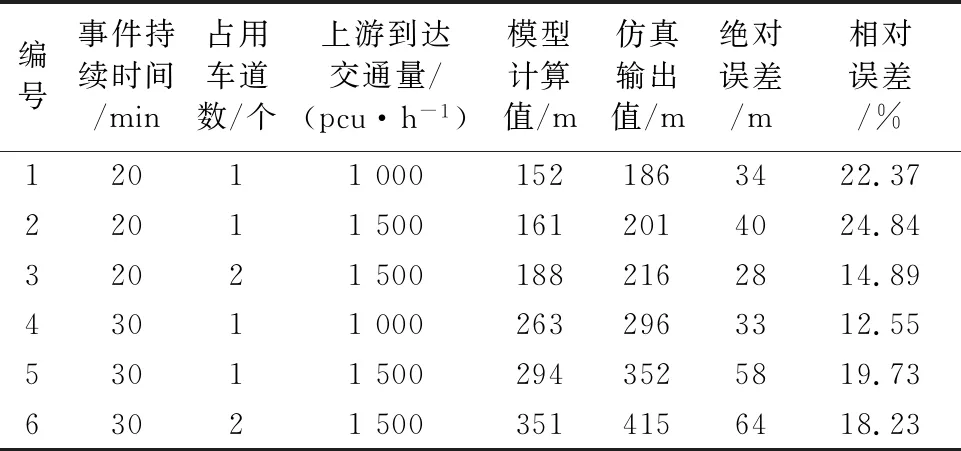
表3 突發事件下的影響范圍預測模型有效性分析

根據對上述四個不同類型的突發事件的仿真值與模型計算值對比可知，仿真值與模型計算值之間絕對誤差的絕對值為42.83 m，相對誤差的平均值約為18.77%.通過對兩個結果的對比，可以這樣認為：本文提出的排隊長度計算模型計算精度較為準確，與仿真結果雖存在一定誤差但可以接受，該模型具有較強的實用性.但是由于只是對簡單路段進行了仿真，且實驗次數偏少，仍需考慮多重因素對不同情況下突發事件進行仿真，再與模型計算值進行對比，不斷優化模型.

4 結 束 語

通過對突發事件后道路交通流的變化情況分析，使用Van Aerde模型作為基礎模型來確定突發事件下交通影響范圍，并對實際道路進行仿真分析，對比仿真結果與模型計算值，得出結論：Van Aerde模型能較好的預測出突發事件的影響范圍，具有一定實用價值.