盾構掘進施工對既有基坑影響的理論分析

盧卓，魏煥衛

(山東建筑大學土木工程學院，山東濟南250101)

0 引言

城市地鐵區間施工方法以盾構法施工為主，盾構規劃路線不可避免的鄰近既有建筑結構，包括地下建筑、樁基、基坑、地下管廊管線等。盾構法施工會擾動土層，從而對周圍環境產生影響，嚴重時會影響生活。針對盾構掘進對周圍環境的影響這一課題，張瓊方等[1]基于Mindlin解計算出盾構產生的附加應力，利用Winkler地基梁，進行疊加得到已建隧道總變形；王濤等[2]運用圓孔擴張—剪切理論，推導了盾構掘進中土體損失產生的附加應力；趙玉勃等[3]基于Mindlin應力解分析了在正面推力和盾殼摩阻力雙重影響下附加應力的分布；武崇福等[4]推導了既有上部荷載下盾構正面推力，盾殼摩擦力和刀盤摩擦力的影響；張潤峰等[5]推導計算了盾構的正面推力、盾殼摩阻力、土體損失對鄰近樁基的附加應力影響；徐林[6]研究盾構隧道開挖對建筑物樁基的影響，分析不同影響因素對建筑物樁基礎的影響變化規律。曾英俊[7]在實際工程的基礎上分析盾構掘進對既有基坑的影響；殷榕鵬[8]考慮開挖過程擠土壓力及摩擦軟化效應影響，對既有隧道因新建隧道的施工所產生的的內力的影響進行研究。

文章基于盾構掘進施工實際工況，研究了盾構掘進施工產生的附加應力對鄰近既有基坑的影響，利用Mindlin應力解[9]推導盾構正面推力和盾殼摩擦力產生作用在接觸面上的附加應力；采用Sagaseta解[10]推導土體損失產生的附加應力，結合三者得到對基坑作用附加應力解答，并與工程實測數據進行對比。

1 盾構掘進附加應力的計算

1.1 盾構掘進對支護結構影響的力學模型及假定

盾構掘進過程是一個考慮時間、空間因素的過程，受擾動土體與盾構間的作用十分復雜。根據盾構掘進施工對周圍土體影響的因素不同，可分為正面附加推力、盾殼側摩阻力和土體損失3個主要因素作用產生的影響，如圖1所示。為反映盾構掘進中主要因素對鄰近既有基坑的附加應力的影響，作如下假定:

(1)假定土體為均勻各向同性的彈性半無限空間體，不考慮盾構和基坑開挖后邊界條件的改變；

(2)假定正面推力為圓形均布荷載，盾殼摩阻力沿掘進方向分布，且分布均勻。

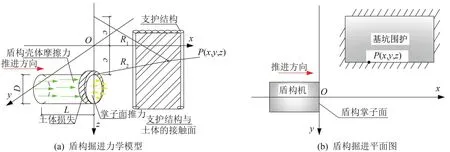
圖1 盾構掘進示意圖

1.2 掌子面推力、盾殼側摩阻力土體損失的取值計算

1.2.1 掌子面附加推力fs的取值

趙玉勃等[3]和吳崇福等[4]僅將正面推力fs取為定值進行計算，不能完全表示對地層影響的盾構正面推力。王洪新[11]在擠土效應等的影響下提出刀盤附加接觸應力求解公式，由式(1)表示為

式中:Δp′為開口的切入擠壓力，kPa，取10～25 kPa；Eu為不排水彈性模量，kPa；ν為掘進速度，cm/min；w為刀盤轉速，rad/min；k為閉口部分幅數，個；D為刀盤直徑，m；ξ為刀盤開口率，%；μ為泊松比。

1.2.2 盾殼摩阻力fm的取值

趙玉勃等[3]和吳崇福等[4]將fm取為定值，但盾殼摩阻力依據地層土體等條件的不同摩擦力并不相同，朱合華等[12]在考慮自重和周圍土體壓力下進行簡化，提出求解公式由式(2)表示為

式中:u為摩阻力系數；φ為土體的內摩擦角，°；γ為土體重度，kN/m3；c為盾構頂部埋深，m；W為盾構單位長度自重，kN/m；Pv、Ph分別為土體自重和側向土壓力，kPa；H為盾構軸線埋深，H=c+D/2，m。

砂和砂礫中的動態摩阻力系數取為0.3～0.4，而將黏土中的動態摩阻力系數取為0.2～0.3[13]。

1.2.3 土體損失Vloss的取值

盾構實際開挖面一般要比盾構機實際尺寸大，實際開挖面與盾殼間的間隙可以視為土體損失。土體損失計算模型有許多種，魏綱[14]在Lee等[15]提出的內切圓的模型基礎上推導后，得到統一的土體損失模型，如圖2所示，在這一模型基礎上進行土體損失的計算。土體損失Vloss由式(3)表示為

式中:g=αGP+U3D+ω，其中GP為開挖面與盾構機間的幾何空隙，m；α為空隙注漿折減系數，取值見文獻[14] ；U3D為盾構前的土體三維彈塑性變形，假設土體為彈性半無限空間體，U3D=0；ω為施工因素，取值見文獻[15] 。

圖2 內切圓模型圖

1.3 正面附加推力產生附加應力的計算

基于Mindlin應力解[9]，在盾構掘進正面推力的圓面上進行積分，求解得到正面推力fs引起支護結構與土體接觸面上任一點P(x，y，z)的附加應力，如圖1所示，垂直作用在支護結構上的附加應力σy1的解析解由式(4)表示為

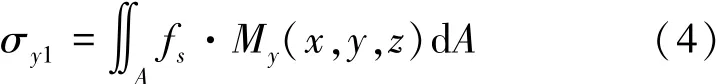
式中:My(x，y，z)為y向的應力影響系數；A為面積微元。

在Mindlin應力解中，應力可以表示為作用力與其應力影響系數My(x，y，z)乘積。My(x，y，z)由式(5)表示為

式中:c0為作用力點的埋深，m；x、y分別為所求點距作用點的x、y向間距，m；z為所求點的深度，m；R1、R2分別為計算點至力作用點的距離和計算點至力作用點沿xOy面對稱點的距離，m，如圖1所示，R1=

在盾構掌子面的圓域上運用數值積分的方法進行積分。依據實際積分條件，將直角坐標轉換為極坐標，如圖3所示。具體轉換關系由式(6)表示為

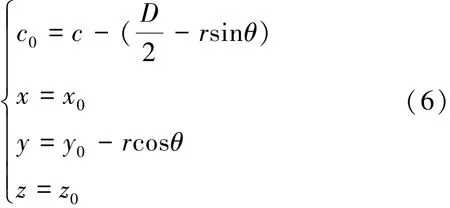
式中:x0、y0、z0分別為x、y、z坐標轉換后的值；r為積分半徑，m；θ為積分角。

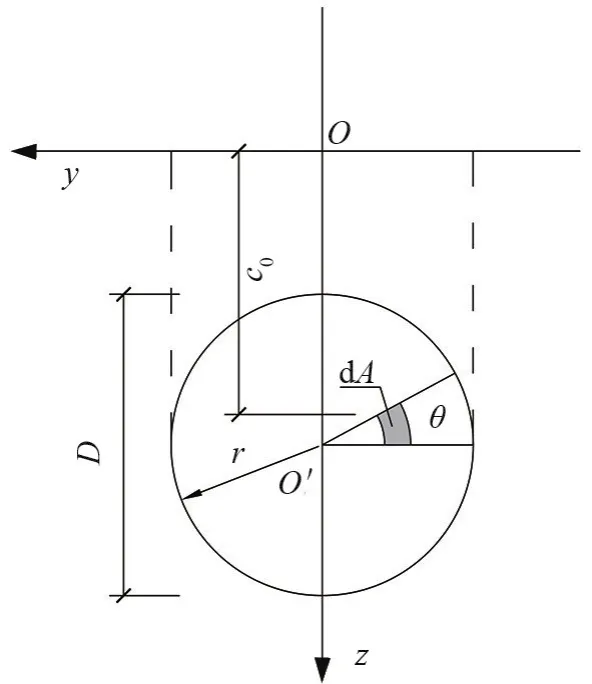
圖3 圓面積分示意圖

將坐標轉化關系(6)帶入式(4)中進行數值積分，得到式(7)為

式中:Fy1為掘進正面力作用在接觸面上的附加荷載，kN/m，；σy1為作用在接觸面上的附加應力，kPa；Aij為微元面積，m2；d為支護結構計算長度，m；k為劃分份數。

利用式(7)可得到正面推力作用在支護結構上沿深度方向的附加線荷載。

1.4 盾殼側摩阻力產生的附加應力的計算

基于Mindlin應力解[9]，在盾殼的側摩阻力的圓柱側面上進行積分，求得盾殼側摩阻力fm引起支護結構與土體接觸面上任一點P(x，y，z)的附加應力，如圖4所示。垂直作用在支護結構上的附加應力σy2的解析解由式(8)表示為

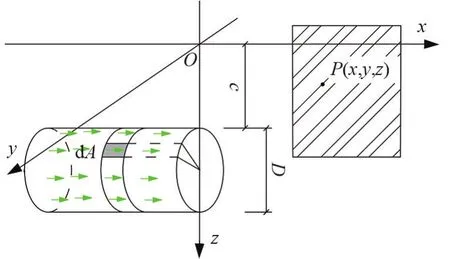
圖4 盾殼積分示意圖

同樣，采用數值積分的方式進行積分。依據實際情況對坐標系進行轉化，如圖4所示。轉化關系由式(9)表示為

將坐標軸轉化關系(9)帶入式(4)中進行數值積分，得到式(10)為

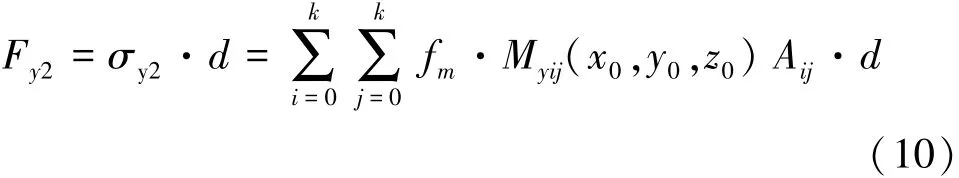
式中:Fy2為盾殼摩阻力fm作用在接觸面的附加荷載，kN/m；σy2為作用在接觸面上的附加應力，kPa。

利用式(10)可得到盾殼摩阻力fm作用在支護結構上沿深度方向附加線荷載。

1.5 土體損失產生的附加應力的計算

張潤峰等[5]為避免鏡像法的復雜，在 Pinto等[16]推導盾構土體損失引起地層位移解的基礎上，利用彈性力學公式求解盾構施工土體損失對樁基礎產生的附加應力解析解。

通過Sagaseta等[10]推導的某點產生的土體損失為基礎，推導求解適用于作用在接觸面上的點P(x，y，z)的三向解析解，如圖5所示。

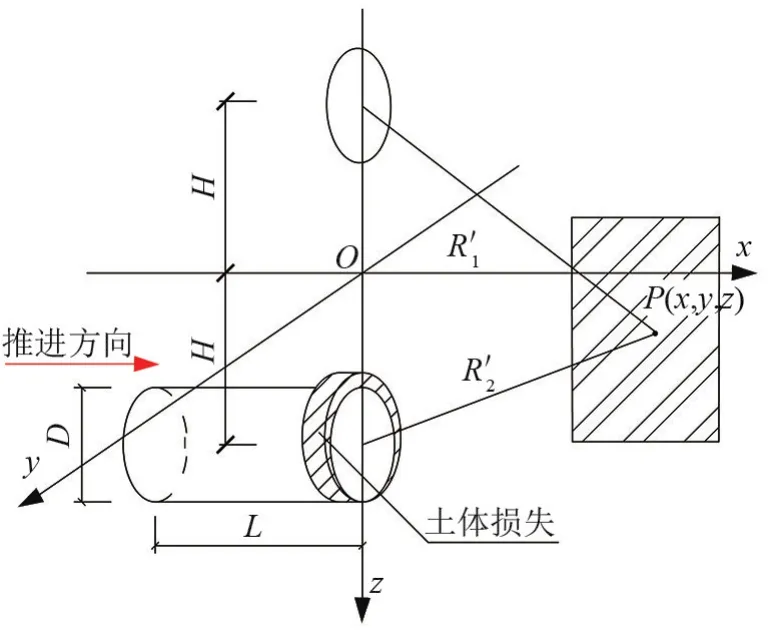
圖5 土體損失示意圖

計算點P的位移分量由時式(11)表示為

式中:sx、sy、sz分別為計算點P的x、y、z向的位移分量，m；R′1、R′2分別為計算點至力作用點的距離和計算點至力作用點沿xOy面對稱點的距離，m。R′1、R′2由式(12)表示為

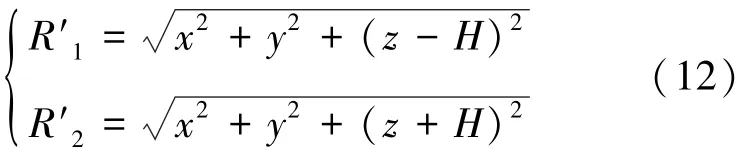
對計算的三向變形sx、sy、sz進行微分，帶入廣義胡克定律并沿盾構積分得到式(13)為

式中:Fy3為土體損失作用在接觸面上的附加應力，kN/m；G為剪切模量，MPa；E為彈性模量，MPa；d為土體與支護結構的接觸面上的計算長度，m；σy3為作用在接觸面上的附加應力，kPa。

利用式(13)可得到土體損失作用在支護結構上沿深度方向的附加線荷載。

2 盾構掘進施工附加應力對既有基坑影響分析

基坑支護結構與單樁或樁基[5-6，17]不同，樁基是土中的基礎構件，土中x、y、z三向附加荷載都會使單樁產生位移，而基坑支護主要受垂直于基坑內部的荷載(即y方向的荷載)的影響，而x、z方向荷載影響不大。當盾構在支護結構一側施工時，只考慮y方向的附加荷載Fy對支護結構的影響。作用于支護結構上的計算長度附加荷載Fy由式(14)表示為Fy=Fy1+Fy2+Fy3(14)

2.1 算例概況

張冬梅等[18]對黃浦江觀光行人隧道出入口豎井基坑一側盾構施工的監測數據進行了分析整理。盾構外徑為6.2 m，盾構襯砌管片壁厚為0.35 m，管片縱向長度為1 m，機身長度為8 m，盾構隧道頂部標高距地表18.13 m，豎井基坑與規劃盾構路線最近距離為3 m；端頭井基坑開挖深度為22 m，當開挖到15.5 m時，因盾構的掘進而停止開挖；圍護結構為地下連續墻墻厚為0.8 m，深為37 m。鋼管支撐型號為X609，厚為11 mm；標準段、端頭井分別設置六道、七道支撐；平面設置間距約為3 m，如圖6所示。土體的物理學參數見表1。

圖6 施工平面圖/mm

表1 土體的物理力學參數表

根據實際工程確定相關計算參數的取值，盾構掘進的掘進速度為 0.35 cm/min，刀盤轉速為0.2 rad/min，閉口部分幅數為 4，掌子面壓力為388 kPa，側摩阻力為57 kPa，泊松比為0.3，土層加權重度為18.4 kN/m2，加權內粘聚力為11.33 kPa，加權摩擦角為23°。利用推導的解析解進行計算分析并與實測數據進行對比。

2.2 盾構掘進對既有基坑附加應力影響分析

2.2.1 支護結構的附加應力實測對比分析

取深度-20 m進行計算和比較。盾構掘進所產生的作用在支護結構上的附加荷載與實測土壓力進行比較，如圖7所示。圖7中nD為支護結構接觸面計算點與掌子面x方向水平距離，如圖1所示。

沿盾構掘進方向，當x＞0時，實測數據與計算數值相比差別較小，隨盾構的掘進，作用在支護結構上的附加荷載增加，數值計算在x=0.25D時，達到最大值，隨之開始減小；實測數據在盾構恰好經過時，達到最大值。0＜x＜0.5D時，實測數據與計算數值的附加應力具有差異，這是由于進行數值計算時，Mindlin應力解和Sagaseta解均假設土體為線彈性體，而實際土體為非線彈性體，與實際情況差別較大，土體受盾構正面推力產生的擠壓作用和側摩阻力產生的剪切作用，導致土體發生變形。上海黃浦江地區以軟土為主，在盾構掘進產生的附加應力的擾動影響下，只能恢復少部分彈性部分的變形。

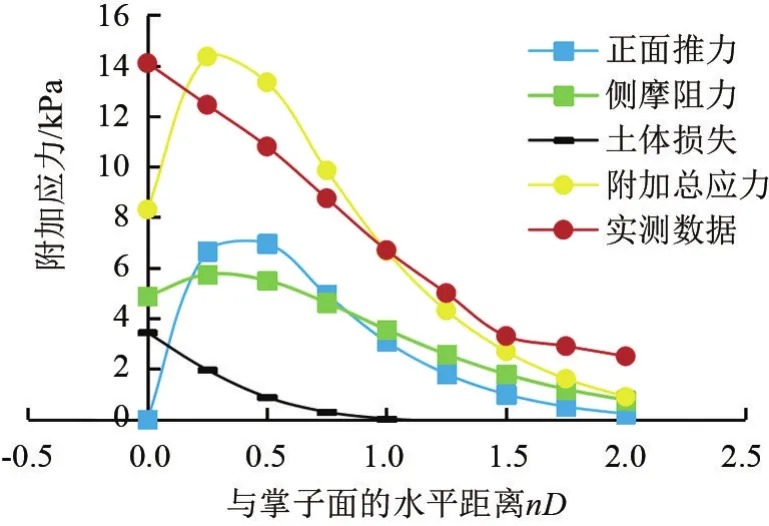
圖7 土壓力對比圖

x＞1.0D時，fm＞fs，fm為支護結構的主要影響因素；0.25D＜x＜0.75D時，fs＞fm，fs為支護結構的主要影響因素，fm與fs的大小都隨水平距離的減小而增加，fm初始值＞fs初始值，但fm增加速度比fs慢，靠近掌子面位置fs＞fm。土體損失產生的附加應力自1.0D開始增加，隨距離的減小而增大。x=0時位于掌子面位置，土體損失產生的附加應力為3.2 kPa，對支護結構的影響發揮次要作用。附加總應力在2.0D處影響開始由0增加，到0.25D增加到最大值，由于0.25D后，fs減小到0，fm減小，總應力隨之減小。

正面推力為圓面荷載，對土體以擠壓作用為主，x=0時，附加應力為0，隨距離的增加先增加后減小；摩阻力為盾殼圓柱面荷載，對土體以剪切作用為主，產生的附加應力隨距離的增大，先增加后減小；側摩阻力與正面推力對土體的作用不同，從而附加荷載曲線不同。

計算值與實測數據進行比較，計算值的最大值出現在0到0.5D之間，實測數據的最大值出現在掌子面位置，數值上二者相差不大；沿掘進方向，在掌子面前計算結果與實測數據的附加應力最大值差別不大，可按照計算最大值進行驗算。

2.2.2 正面推力與側摩阻力產生的附加荷載

正面推力和側摩擦力產生的附加應力，如圖8所示。正面推力與側摩擦力產生的附加應力最大值出現在盾構軸線 -21 m處，沿深度方向，向上下兩側逐漸減小。

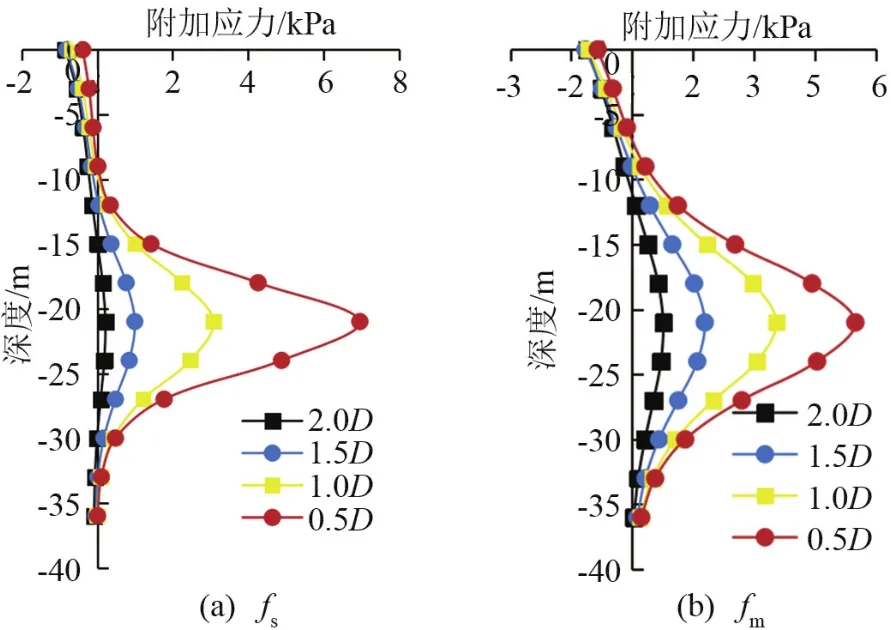
圖8 正面推力和側摩擦力附加應力圖

正面推力產生的附加應力fs比側摩阻力產生的附加應力fm減小速度要快；由2.0D到0.5D，fs變化幅度較大，fm變化幅度小；在0.5D處fs的最大值大于fm的最大值，此時fs對基坑支護結構的影響發揮主要作用，x＞1.0D時，fs的最大值小于fm的最大值，此時fm發揮主要作用。

2.2.3 土體損失產生的附加荷載

土體損失產生作用在支護結構上的附加荷載，如圖9所示。土體損失產生的附加應力的最大值在盾構軸線位置-21 m處。x＜1.0D時，盾構掘進引起土體損失擾動，周圍土體的附加應力開始增大，在盾構軸線深度處增加最為明顯，附加應力值沿深度方向向上兩側減小，減小速度很快。與fs和fm在數值上相比較，數值較小不發揮主要作用。

圖9 土體損失附加應力圖

2.3 支護結構的變形增量分析

x=0.5D時，荷載增量較明顯，按0.5D位置處計算支護結構的側移增量。將計算結果與實測結果進行對比，如圖10所示，計算結果比實測結果數值上要小，基坑在深度為15.5 m處暫停開挖，開挖完成部分設多道支撐，上部變形增量較小，隨支護結構的深度增加，側移增量先增加，后減小，支護結構底端變形增量減小為0。

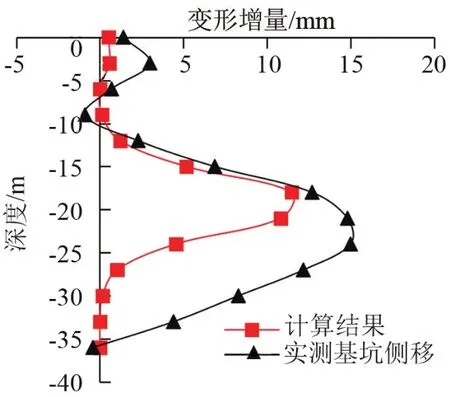
圖10 側移對比圖

對比分析解析解計算結果與實測結果，發現二者的變化趨勢規律相似。解析解計算結果在-18～-22 m某處達到最大值，此時盾構掘進產生的附加荷載最大，對支護結構的影響最明顯，在 -25 m處地下連續墻的變形增量減小，并隨深度增加趨近于0；實測結果中板樁墻的變形增量在 -25 m處達到最大值，后開始減小，在 -36 m處減小至0。基坑在深度-15.5 m處暫停開挖，開挖面以上設多道鋼管支撐，可以有效限制地下連續墻的變形，從而15.5 m以上位置變形增量小；15.5 m以下盾構施工的附加荷載增大，過盾構軸線(-21 m)后附加荷載開始減小，支護結構的變形增量隨盾構施工的附加荷載先增加后減小。

計算結果與實測數據規律相同，證明通過所推導的公式進行計算，可以反映盾構支護結構的側移變化規律。

3 結論

基于Mindlin應力解，推導盾構正面推力和盾殼摩擦力產生作用在接觸面上附加應力，并基于Sagaseta基本解推導了盾構掘進過程土體損失產生的附加應力，并通過實測數據與計算結果進行對比，得到如下結論:

(1)隨盾構掘進靠近支護結構接觸面計算點，支護結構所受的附加應力也在不斷增大；當盾構不斷遠離計算位置時，附加應力在減小。沿盾構掘進方向公式求解計算的附加應力值與實測數據在掌子面前(x＞0)相似度較高，在盾構掘進掌子面距支護結構距離x=0.25D位置，支護結構受盾構掘進影響產生的附加應力較大，導致支護結構產生的撓曲變形增大，支護結構最危險、最不利。

(2)沿掘進方向，在掌子面前可按計算值進行計算，0.25D后附加應力開始減小，附加應力最大值與實測最大值差別不大，可按計算值附加應力最大值對支護結構進行驗算。在實際工程中，支護結構受盾構掘進影響而產生的土壓力以及變形量的變化較明顯，應采取基坑停工，坑內堆土等方式保證基坑的安全。

(3)支護結構接觸面計算點與與掌子面的水平間距x＞1.0D時，盾殼摩擦力產生的附加應力fm為支護結構的主要影響因素；計算位置與掌子面的水平間距0.25D＜x＜0.75D時，正面推力產生的附加應力fs為支護結構的主要影響因素；土體損失產生的附加應力自1.0D開始增加，＞1.0D時其值很小可以忽略不計，土體損失產生的附加應力對支護結構的影響發揮次要作用。