創新教育應注重學生思維的引導和開發

朱增成

中圖分類號：G622文獻標識碼：A文章編號：1003-9082（2019）08-0-01

創新教育就是根據創新意識，創新思維、創新能力為主要目標的教育理論，數學課堂教學的創新研究，也逐漸成為許多數學教師關注的話題。由于數學具有應用的廣泛性、理論的抽象性和邏輯的嚴謹性等特點，決定了數學教學不僅是基礎教育的組成部分，也是實施創新教育的主陣地。學生在初中階段存在的主要問題是理解難、應用難。這也是各在課教師頗感頭疼的問題。究其原因是學生思維的深度和廣度不夠，所以教師應在學生思維引導和開展上尋找突破口。

一、注重定義、定理的理解、夯實學生思維開發的基礎

1.“趣”得定理

由于定理理論的抽象性、推理的獨特性， 學生理解較為困難。所以對定理的得到要盡量尋找學生易于觀察、易于發現的方法。

例如，在講授多邊形內角和定理時，由四邊形內角和定理研究方法：過四邊形個頂點作對角線， 可以把四角形分成兩個三角形，

可得：四邊形內角和=2×180 =（4-2）×1800 =3600

引導：五邊形內角和=3×180 =（5-2）×1800 =5400

六邊形內角和=4×180 =（6-2）×1800=7200

開發：n邊形內角和=（n-2）× 1800

2.“活”解定義

學生在許多題目的解答應用時出錯的原因是對定義理解不透好和不靈話而導致，所以看似簡單的定義教學也應突出學生題維引導和開發。

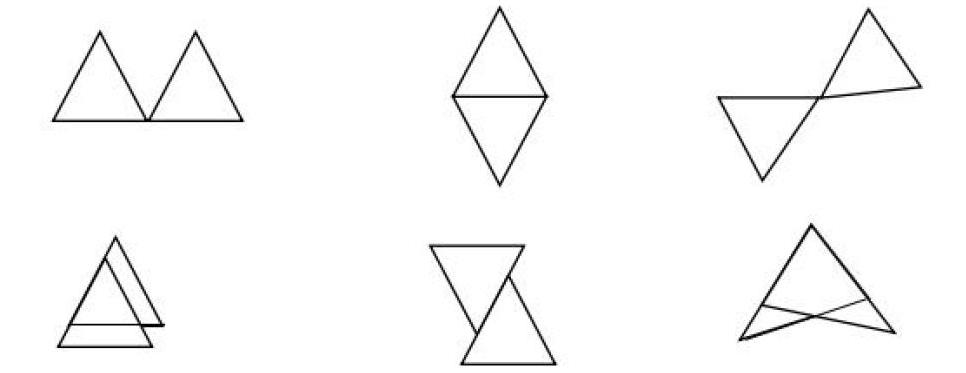
例如：在講授“全等三角形”定義時，可剪下兩個全等三角形，通過如圖那樣變換兩個三角形位置。

進一步抽象成幾何圖形，讓學生找出對應頂點、對應角、對應邊，這樣可以使學生靈活的掌握全等三角形的全等變換形式，加深學生對全等三角形定義的理解，有助于學生在復雜圖形中觀察，尋找出全等三角形。

二、注重例題的變形，引導和開發學生思維的深度

教材例題是幾何定理的初步應用，學生容易理解，但許多題目木身只是例題的簡單變動，學生往往感到束手無策。這說明學生對定理的深度把握不夠，所以以例題為切入點， 變換條件和結論，有助于學生思維深度的開發。

三、注重綜合，拔高訓練，刺激學生思維活力，引導和開發學生思維廣度。

幾何中的綜合拔高訓練題是基礎知識和基本技能的綜合訓練，也是學生學習中最困難的地方，但也是具體體現學生思維閃光點和指導開發學生思維的突破口。

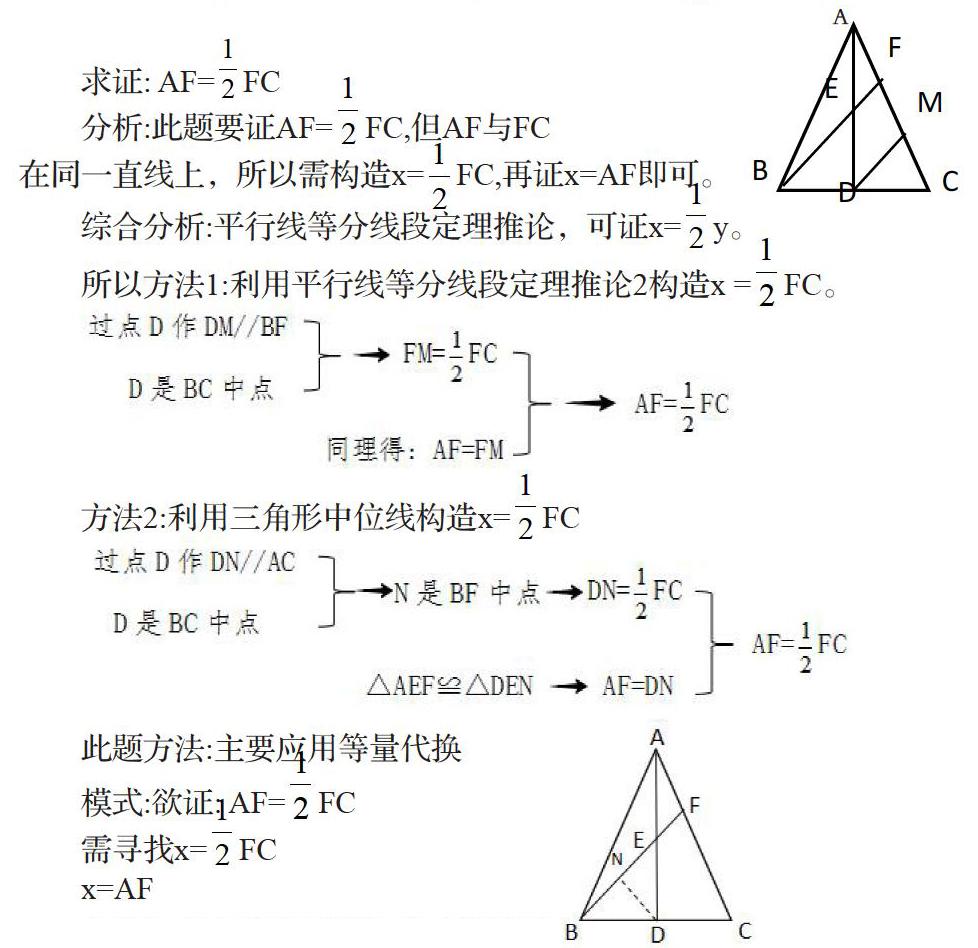
例如：已知： AD是△ABC的中線，E是AD的中點，F是BE的延長線與AC的交點。

求證： AF=FC

分析：此題要證AF=FC，但AF與FC

在同一直線上，所以需構造x=FC，再證x=AF即可。

綜合分析：平行線等分線段定理推論，可證x=y。

所以方法1：利用平行線等分線段定理推論2構造x =FC。

方法2：利用三角形中位線構造x=FC

此題方法：主要應用等量代換

模式：欲證： AF=FC

需尋找x=FC

x=AF

此題屬于由結論證明模式尋找證明方法的題型。

學生感覺綜合題、拔高題、應用題等題型困難的主要原因是方法欠缺，以致思維堵塞。所以這類題型應注重方法指導和點拔，由方法找思路，引導和開發學生思維的廣度和深度，進而培養學生的創新思維能力。

以上三個方面，遵循了學生由易到難，由簡單到復雜，循序漸進的認知規律，突出雙基聯系，更主要培養了學生思維的靈活性，思維的深度和廣度，有力地促進了學生創新思維和創新意識的形成。