插電式混合動力汽車的次優能量管理策略

吳進軍 顏丙杰 方繼根 王西峰 謝志鵬 史 洋 李 亮

1.中機生產力促進中心，北京，1000442.清華大學汽車安全與節能國家重點實驗室，北京，1000843.寧波吉利汽車研究開發有限公司，寧波，3153364.東風汽車集團股份有限公司技術中心，武漢，430058

0 引言

國內外對插電式混合動力汽車整車能量管理策略進行了大量的研究，目前，已提出的控制策略主要有基于規則的啟發式策略[1]、可實時計算的瞬時優化控制策略、基于模型預測的能量管理策略，以及基于最優理論的最優控制策略。

瞬時優化控制策略主要是指等效燃油消耗最小策略(equivalent consumption minimization strategy, ECMS)，其思想是在車輛行駛過程中的每個時刻，實時計算滿足當前駕駛員需求功率中的發動機輸出功率和電機輸出功率分別對應的燃油消耗量和耗電量，將該瞬時的電機耗電量等效為瞬時的燃油消耗量，并獲得當前時刻的等效油耗，求取使得該瞬時燃油消耗最小的發動機和電機的輸出功率(即最優分配策略[2-4])。

模型預測控制(model predictive control, MPC)是一種基于模型的、滾動實施并結合反饋校正的優化控制算法。FU等[5]利用智能交通系統(intelligent transportation systems, ITS)獲得交通流信息，基于MPC提出了一種能量優化算法，分析了預測車速信息的準確度對不同控制策略的影響。

最優控制策略是基于最優化方法或最優控制理論開發出來的混合動力汽車整車能量管理策略，研究最多的是基于Bellman動態規劃(dynamic programming, DP)的控制策略, 動態規劃分為確定性動態規劃(deterministic dynamic programming, DDP)和隨機動態規劃(stochastic dynamic programming, SDP)。

SDP是在DDP的基礎上引入隨機狀態變量發展而來的，通常針對多條工況進行研究。LIN等[6]、LIU等[7]采用SDP對并聯混合動力構型進行能量優化分配；MOURA等[8]系統地討論了可控消耗型策略相對于常規消耗維持型策略的潛在優勢，并討論了油電價格比對SDP優化效果的影響。

目前大多數能量管理策略無論是借助先進的車載終端獲取大量實時的交通數據，或是實時分析駕駛員駕駛意圖，最終目的都是通過優化擋位或功率分配來提高整車燃油經濟性能，但有關同時優化擋位與功率分配的報道較少。本文主要針對電控機械式自動變速器(automated mechanical transmission, AMT)擋位與功率分配同步優化過程中計算量大，以及最優擋位與最優功率分配嚴格一一對應實用性差的問題，提出了一種可實際應用的次優能量管理策略。通過SDP獲得最優的擋位與功率分配；創新地提出了通過算法內部約束與外部修正相結合的雙重擋位約束方法，來避免換擋過程的“反復”，以保證駕駛性能；并采用瞬時優化算法實現換擋過程中的最優功率分配，解決了換擋修正過程中的最優功率分配和擋位不匹配問題，使整個優化算法具有更好的實用潛力。

1 基于AMT的同軸并聯混合動力系統建模

1.1 駕駛員模型

駕駛員模型通常為一個PI控制器模型[9]，輸入為期望車速與實際車速之差，輸出為油門和踏板信號，則加速踏板和制動踏板位置可描述為

(1)

|θ|∈[0,100%]

式中，KP、KI分別為比例系數和積分系數，兩者可通過試錯法來確定；va為實際車速,km/h；vr為期望車速,km/h；θ為踏板開度，加速踏板為正，制動踏板為負。

通過查表得到當前踏板位置θ與AMT輸入軸轉速n,求得駕駛員的需求功率Pr，并構建需求功率MAP圖,見圖1。

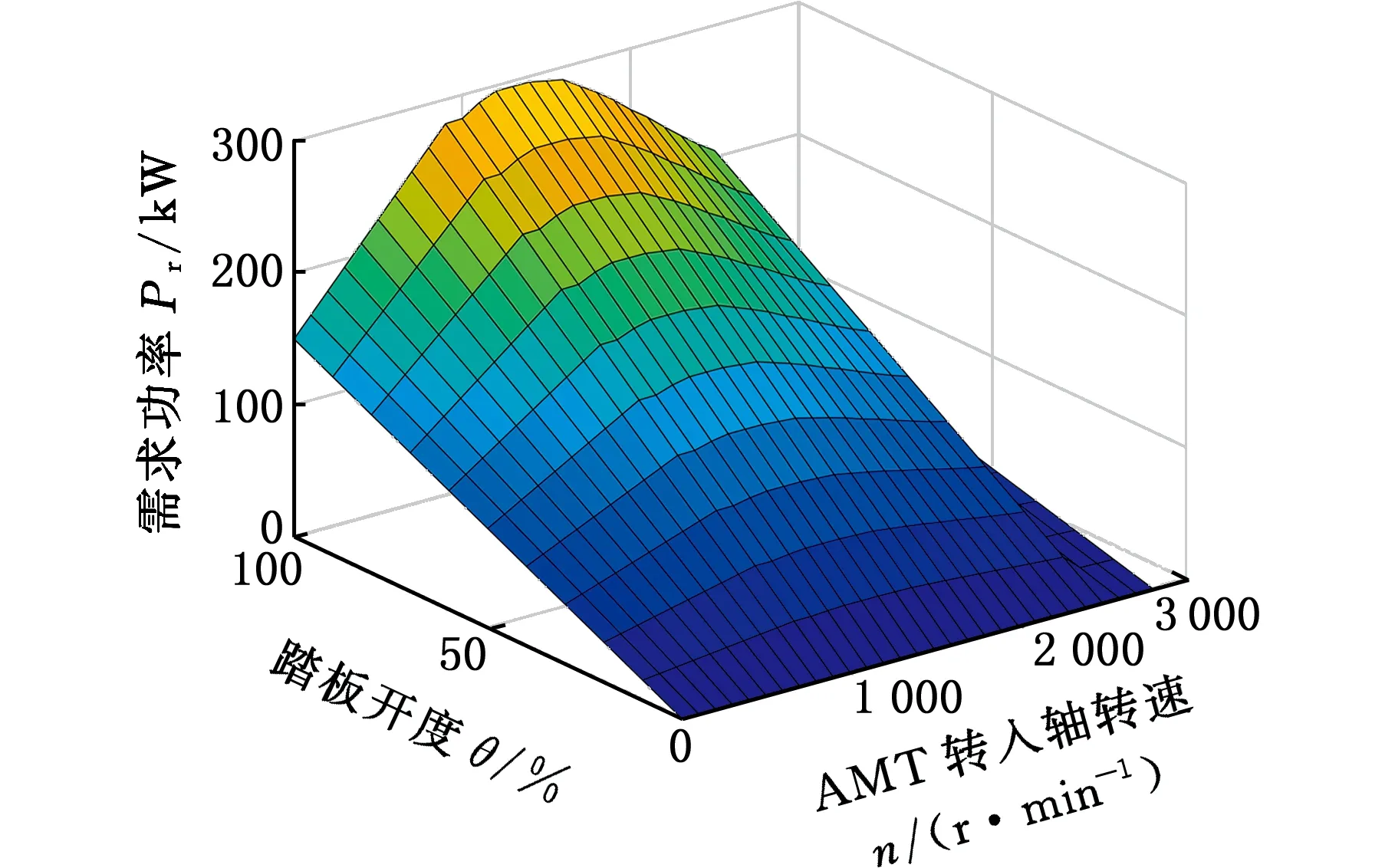
圖1 需求功率Fig.1 The damand power

1.2 發動機模型

為便于優化策略的開發，建立了簡化的面向控制的壓縮天然氣(compressed natural gas, CNG)發動機模型，單位時間內的CNG消耗量可表示為

(2)

式中，Qcng為單位時間內的CNG消耗量,mL/s；Te為發動機輸出扭矩,N·m；ωe為發動機角速度，rad/s；Pe為發動機輸出功率,W；ρcng為CNG密度，kg/m3；g為重力加速度，本文取9.8 m/s2；b為CNG消耗率，可通過一定轉速和轉矩查找準靜態發動機萬有特性MAP圖得到。

1.3 電機模型

在運行過程中，電機既可作為電動機工作，也可作為發電機工作，與發動機模型相似，電機功率計算模型可表示為

(3)

式中，Pm為電機功率，W；Tm為電機輸出扭矩，N·m；ωm為電機角速度，rad/s；ηm為電機效率，可通過一定轉速和轉矩查找電機準靜態效率MAP圖得到。

1.4 動力電池模型

忽略電池壽命及溫升影響，將動力電池簡化為開路電壓串聯一個內阻的等效電路，見圖2。

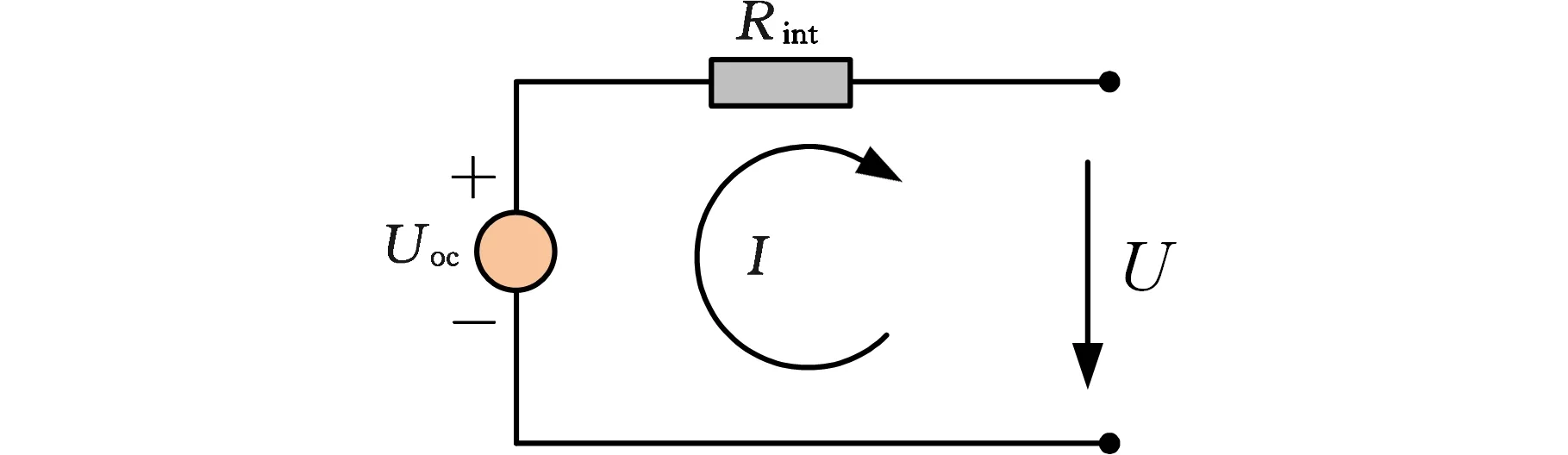
圖2 動力電池等效電路Fig.2 Power battery equivalent circuit diagram

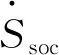
(4)

式中，Uoc為開路電壓；Qbat為電池容量，A·h；Rint為電池內阻，Ω；Pele為電池功率，W；Rdis、Rchg分別為放電狀態和充電狀態下的電池內阻，Ω。

1.5 動力學模型

汽車行駛過程的受力示意圖見圖3，汽車縱向動力學平衡方程為

(5)

式中,Ttq為作用在車輪上的驅動力矩，N·m；Tb為作用在車輪上的制動力矩，N·m；m為整車總質量，kg；f1、f2分別為第一和第二滾動阻力系數；v為車速，m/s；CD為空氣阻力系數；ρair為空氣密度，kg/m3；A為迎風面積，m2；α為道路坡道角，rad；δ為旋轉質量換算系數；r為車輪半徑，m。

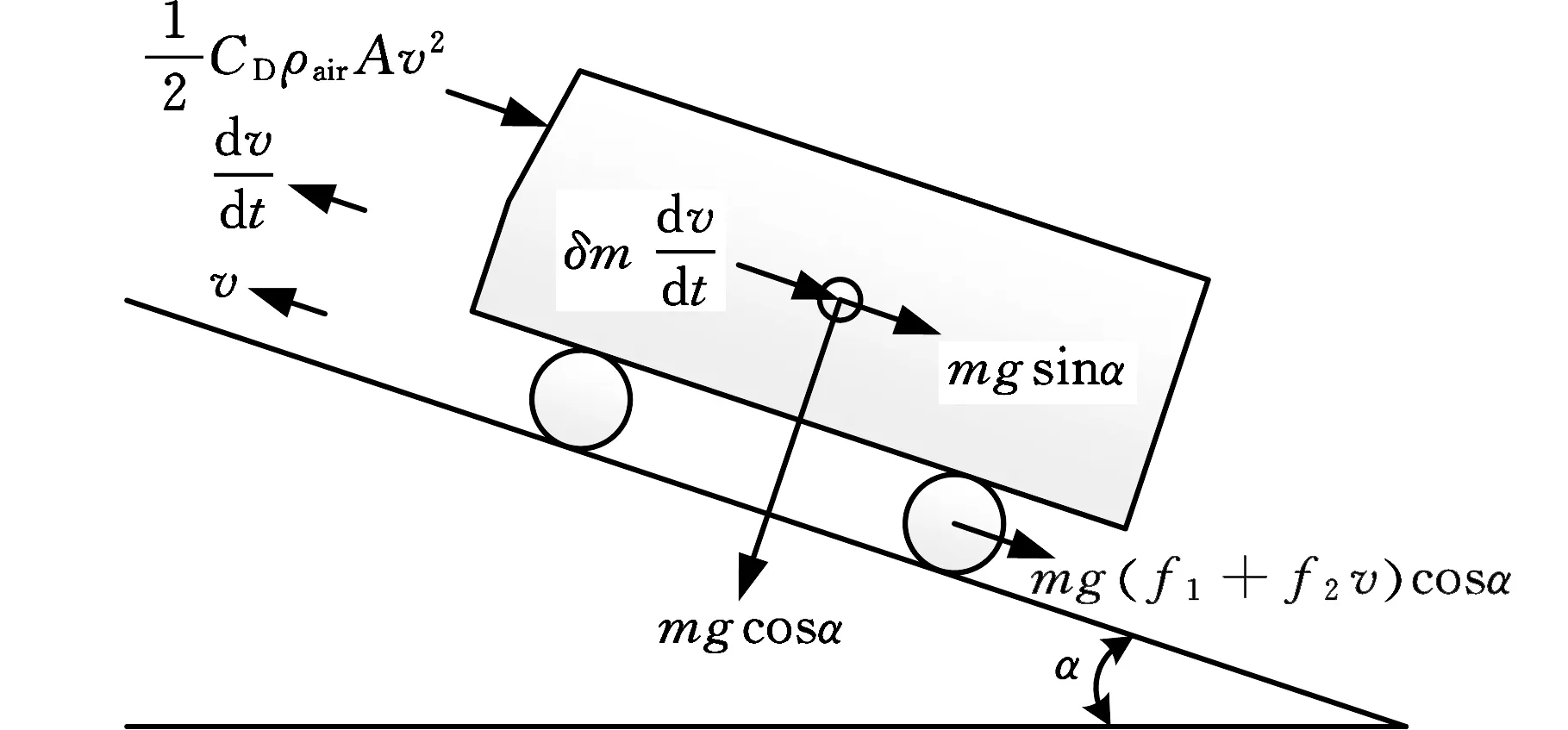
圖3 汽車行駛受力示意圖Fig.3 The schematic diagram of the driving force of a car

2 次優能量管理策略

優化發動機與電機間的功率分配和AMT擋位可最大程度地提高整車的燃油經濟性，但在一定需求功率下，最優功率分配與最優擋位之間嚴格的對應關系在實際應用過程中將難以保證。離線優化所得的最優決策組合(最優功率分配和換擋操作)，在實際應用過程中有可能造成AMT抖振，從而影響駕駛舒適性，故需要對換擋操作進行約束，但此時原有發動機和電機最優分配已無法保證燃油經濟性最優，甚至會惡化其燃油經濟性。針對上述問題，本文提出了一種可實際應用的次優能量管理策略(圖4)，具體步驟如下：

(1)將復雜的4維(需求功率Pr、車速v、SOC值Ssoc、當前擋位)2參數(擋位動作、發動機功率)優化問題轉換為3維(需求功率、車速、SOC值)2參數(目標擋位、發動機功率)優化問題，以減小計算量；

(2)針對最優決策在實施過程中可能出現的頻繁升降擋問題，提出了內部約束與外部修正相結合的方法，在內部優化過程中引入對換擋操作的懲罰項λ，對頻繁換擋進行約束，在外部(即最優結果后處理)研究不同SOC值下的最優換擋曲線，歸納出一般規律；

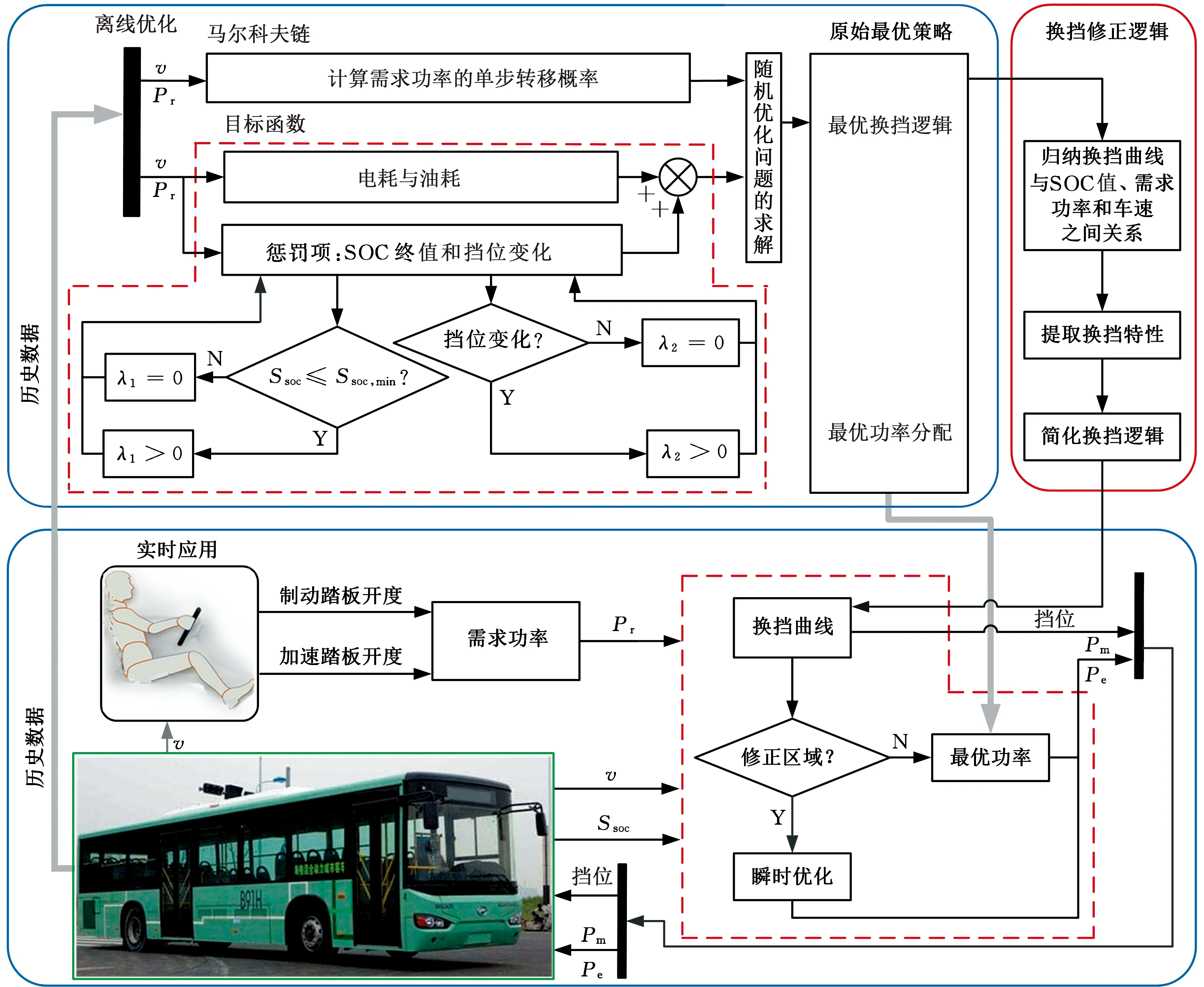
圖4 次優能量管理策略的框架圖Fig.4 Frame of the sub-optimal energy management strategy

(3)對最優擋位進行修正，將最優擋位圖轉化為簡單的二參數換擋邏輯，解決頻繁換擋問題的同時可簡化換擋邏輯；

(4)換擋邏輯的改變使得初始最優功率分配不再適用，此時采取瞬時能量優化控制策略，實時獲取最優功率分配。

最后利用實車采集的工況數據，仿真驗證在不同工況與路況條件下所提策略的有效性。

2.1 隨機駕駛員需求模型

由實車采集得到重慶303公交線路的運行工況數據，根據汽車縱向動力學方程，可計算出相應工況下的變速箱輸入端駕駛員需求功率的變化。選取駕駛員需求功率和車速作為狀態變量，并將其離散化，即

(6)

式中，NPr為需求功率的離散個數；Nv為車速的離散個數。

駕駛員需求功率的單步轉移概率可描述為：在當前需求功率和當前車速條件下，下一時刻需求功率出現的概率，其表達式為

(7)

i,j=1,2,…,NPrl=1,2,…,Nv

利用最大近似值原理，需求功率的單步轉移概率可通過數據統計獲得，即

(8)

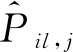
在數據統計過程中，數據取整或離散精度不高時易導致需求功率邊界值(如最大值或最小值)僅出現一次(即Mil=0)，為方便計算，規定下一時刻需求功率將以100%的概率向相同狀態轉移。

2.2 隨機優化問題的形成

采用SDP優化需求轉矩的分配，離散狀態變量可表示為

xk={Ssoc,k,Pr，k,vk}

(9)

式中，xk為優化過程中的第k步狀態變量集合；Ssoc,k為第k步電池SOC的離散值；vk為第k步車速的離散值；Pr,k為第k步需求功率的離散值。

狀態變量Pr以概率矩陣的形式隨機轉移，得到電池SOC和車速的離散狀態方程分別如下：

(10)

(11)

ck=mgf1cosαk+mgsinαk-

式中，Δt為時間步長。

同時選取控制變量如下：

uk={Pe,k}

(12)

式中，uk為優化過程中的第k步控制變量集合；Pe,k為第k步發動機功率離散值。

由于動力系統的限制，上述狀態變量和控制變量必須滿足如下約束條件：

(13)

式中，ωm,min、ωm,max分別為電機的最小和最大角速度，rad/s；ωe,min、ωe,max分別為發動機的最小和最大角速度，rad/s；Pm,k、ωm,k分別為第k步的電機功率和角速度；Pm,min、Pm,max分別為角速度ωm時的電機最小和最大功率，kW；Pe,k、ωe,k分別為第k步的發動機功率和角速度；Pe,min、Pe,max分別為角速度ωe時的發動機最小和最大功率，kW；Ssoc,min、Ssoc,max分別為電池SOC值的下限和上限。

由于系統具有時不變特性以及運行過程無終端時間約束，因此可將混合動力系統能量管理建立為一個無限時域優化問題。在約束條件下，尋找最優的控制變量，使得目標函數在無限時間域內的期望最小，并建立如下目標函數：

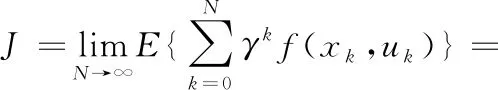
(14)

式中，J為目標函數(即代價函數)；E為期望函數；Ssoc,e為期望的終端SOC值；pcng為CNG的價格,元/kg；pele為電價,元/(kW·h)；Pele為電池功率，W;f為單步代價函數；γ為折扣因子，滿足γ∈[0,1]；λ1、λ2分別為SOC和擋位的懲罰因子;gp,k+1、gp,k分別為第k+1步和第k步的擋位值。

2.3 隨機優化問題的求解

本文主要采用值迭代法進行求解[10-12]，該方法與DDP相似，在每一個狀態離散點遍歷所有可能的需求分配以獲得最優的決策變量。迭代求解過程見圖5。

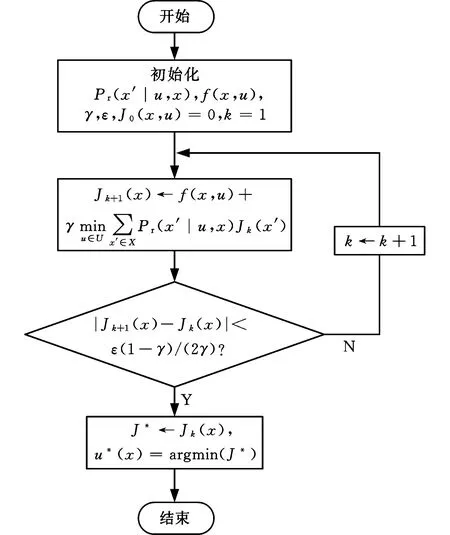
圖5 迭代求解過程Fig.5 The iterative solution process

(1)算法初始化。設定折扣因子γ=0.95，指定錯誤容差ε=1%，初始目標函數J0(x,u)=0，迭代次數k=1。

(2)貝爾曼迭代。在每一個狀態變量x和控制變量u下，將目標函數表示為貝爾曼迭代方程的形式，即

(15)

式中，X為離散的狀態變量可行域；U為離散的控制變量可行域；x′為在控制變量u下，狀態變量x轉移到的新狀態。

(3)終止條件判斷。判斷相鄰兩次迭代的目標函數值之差是否滿足終止條件，即

|Jk+1(x)-Jk(x)|<ε(1-γ)/(2γ)

(16)

若滿足終止條件，即代價函數收斂到最優，則令最優目標值J*=Jk(x)，進入步驟(4)；否則，返回步驟(2)。

(4)求解最優控制策略。最優控制策略即為使目標函數收斂時的控制變量，可表示為

u*(x)=arg min(J*)

(17)

3 仿真分析

3.1 仿真工況及優化結果

基于大量歷史工況數據，采用SDP獲得最優擋位與最優功率分配，其中在Ssoc=40%狀態下的換擋策略與最優發動機功率分別見圖6和圖7。

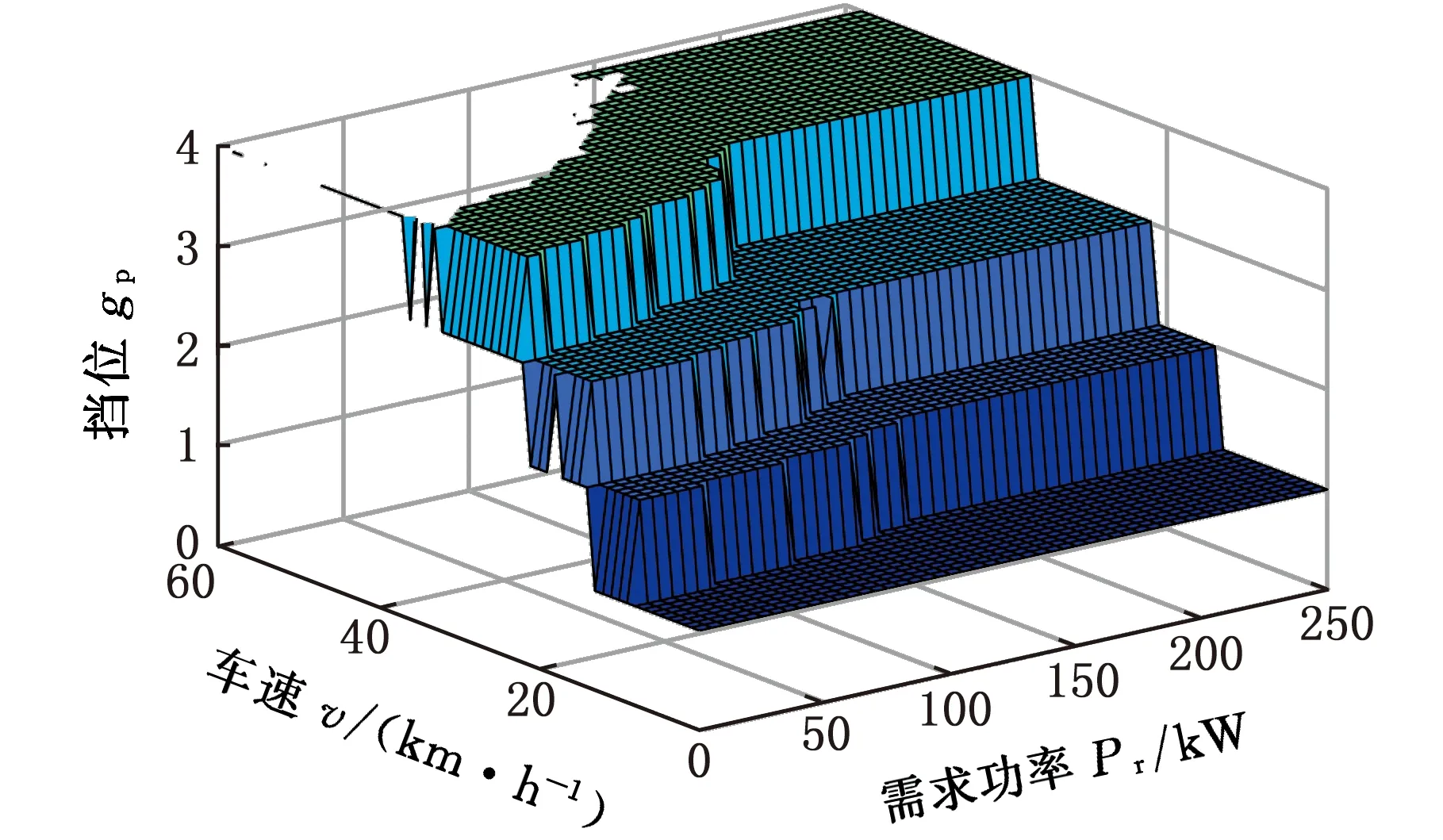
圖6 最優擋位(Ssoc=40%)Fig.6 Optimal position(Ssoc=40%)

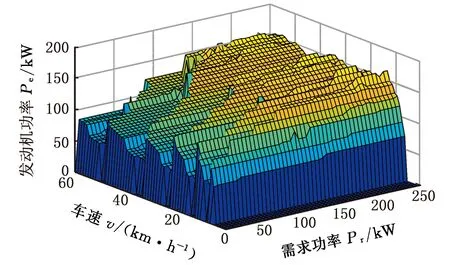
圖7 最優發動機功率(Ssoc=40%)Fig.7 Optimal engine power(Ssoc=40%)

由圖6可以看出，在Ssoc=40%狀態下，不同擋位之間有明顯的分界線，與實際過程中常用的二參數換擋曲線類似[13-14]。此外，該換擋曲線在一定車速范圍內，隨著需求功率的增大，表現出延時升擋的特性，相較于固定的一條換擋曲線具有更優異的動力性能。

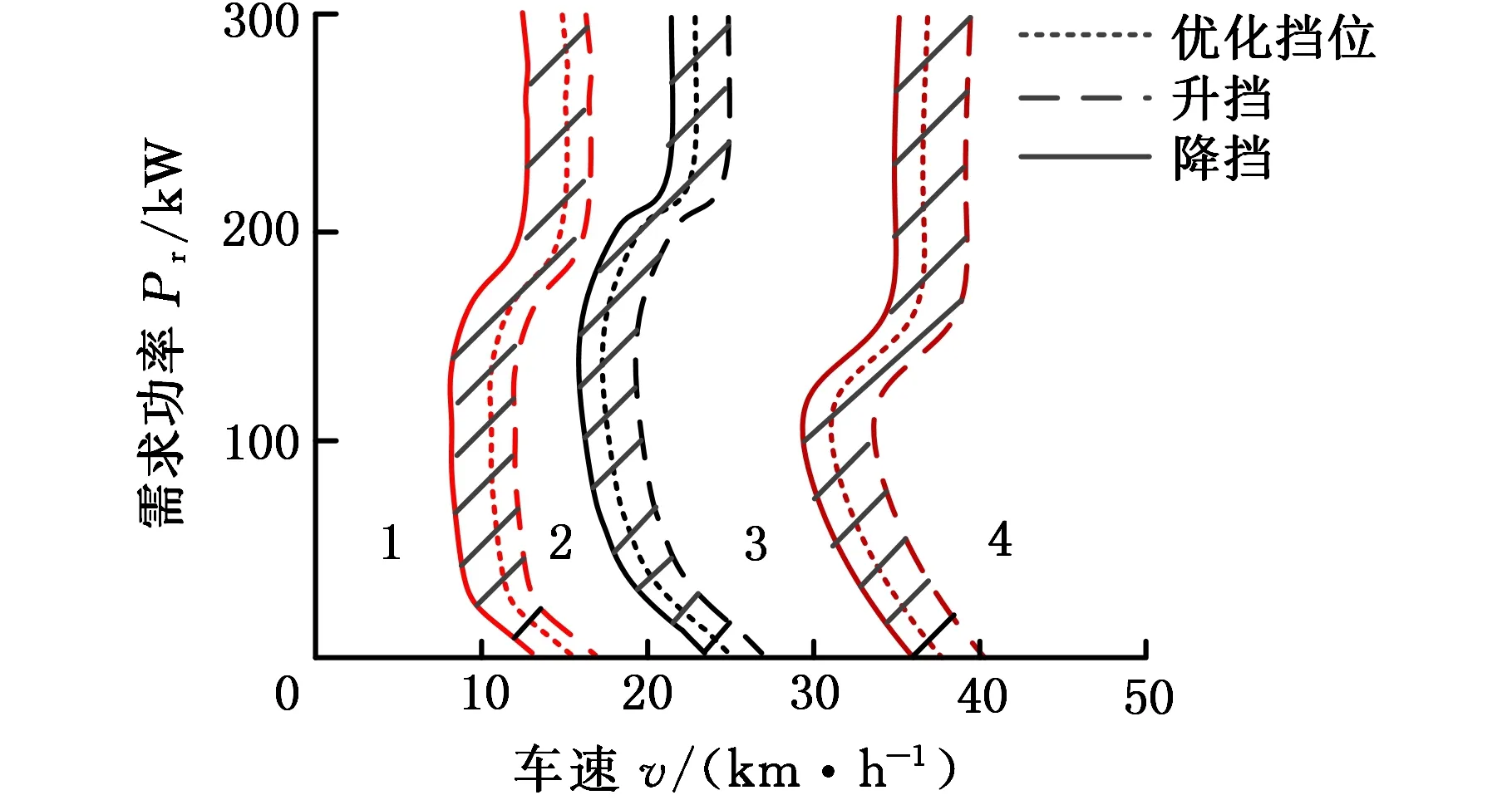
圖8 修正的換擋曲線Fig. 8 Modified shift curve

通過研究不同SOC狀態的換擋曲線，可構建完整的換擋曲線來分析，見圖8。以1擋→2擋換擋曲線為例,點線為通過SDP優化算法獲得的最優換擋曲線，其左側為1擋，右側為2擋；通過修正邏輯得到升降擋曲線，實線為降擋曲線，虛線為升擋曲線；因此在降擋曲線左側和升擋曲線右側的區域，其擋位與SDP優化的擋位結果一致，最優功率通過查表最優功率分配獲得；在擋位陰影部分以內的區域，則采用瞬時優化控制策略實時獲取最優功率分配。

3.2 與不同控制策略的對比分析

所采用的仿真工況為實車采集重慶303路公交車運行數據，線路共有33個站點。該公交運行工況的速度-時間曲線見圖9。

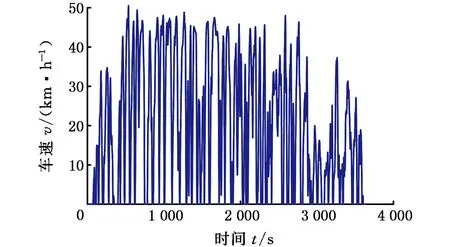
圖9 公交工況的速度-時間曲線Fig.9 The speed-time curve of bus condition

為驗證所提方法換擋策略的有效性，將基于測試工況與基于常規換擋策略的EV-CS策略進行對比，仿真結果見圖10。為分析所提方法對整車燃油經濟性改善的效果，將采用所提方法構建的換擋策略，分別與EV-CS策略、ECMS策略以及DP策略進行對比[15-16]，見圖11。為保證對比的有效性，所采用的對比策略與所提策略具有相同目標函數中的單步代價函數f(x,u)。

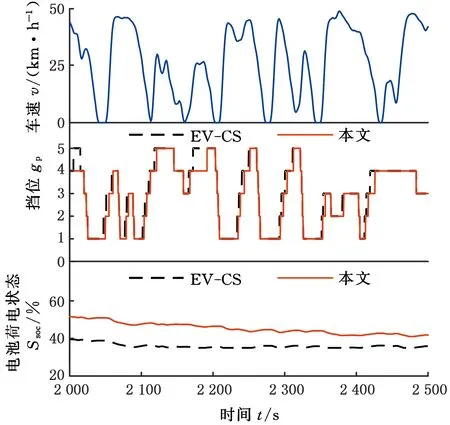
圖10 換擋曲線對比Fig.10 Gear curves of simulation

由圖11可以看出，4種控制策略均基于相同的車速工況(該工況為圖9的返程工況)，且4種控制策略的電量均在最后耗盡。由SOC值-時間曲線可知，EV-CS策略優先耗電，而在電量維持階段(Ssoc=40%)的時間最長，因此，EV-CS策略在初期的氣耗較低，在后期的氣耗變高；DP策略基于全程工況完全已知的假設，具有全局優化性能，因此該策略可將電能在全程進行平衡；ECMS策略為瞬時最優策略；本文所提策略引入了隨機狀態變量，是一種基于SDP的預測控制策略。與ECMS策略相比，本文所提策略的優化結果考慮了未來一段時間的工況變化情況；與針對單一工況的DP策略相比，所提策略的優化過程是基于狀態概率的轉移，優化結果本質上是針對多條工況“平均意義上”的最優，更具有實際應用意義。不同控制策略下的終點SOC、氣耗、電耗和費用見表1。由表1可知，本文所提策略的燃油經濟性有顯著的提升效果。

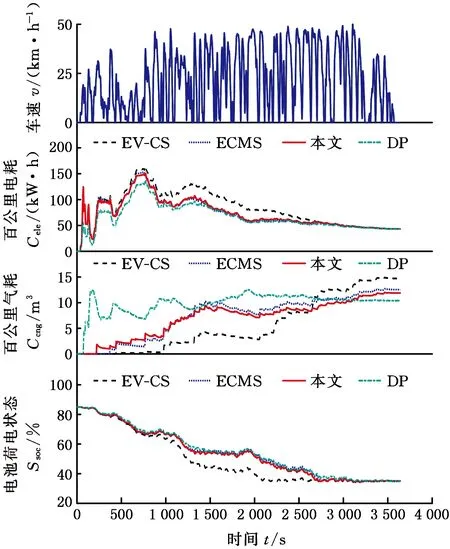
圖11 仿真結果對比Fig.11 Comparison of simulation curves

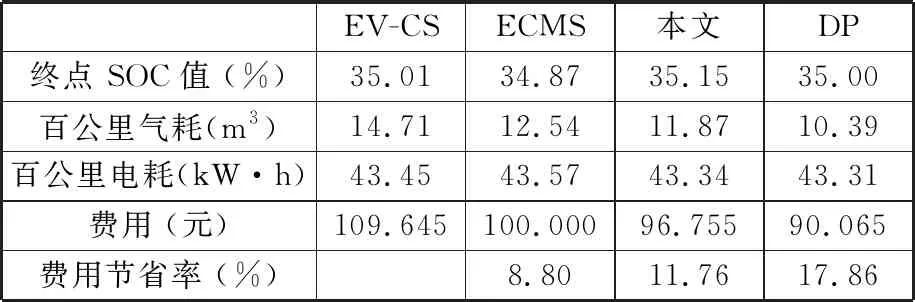
EV-CSECMS本文DP終點 SOC值 (%)35.0134.8735.1535.00百公里氣耗(m3)14.7112.5411.8710.39百公里電耗(kW·h)43.4543.5743.3443.31費用 (元)109.645100.00096.75590.065費用節省率 (%)8.8011.7617.86

4 結論

(1)本文基于隨機動態規劃方法，提出了面向實際應用的次優能量管理策略。隨機動態規劃算法在確定性動態規劃的基礎上引入了隨機過程，使得優化過程變得更為復雜，但隨機動態規劃生成的優化結果是以表格的形式存儲的，且其優化結果是車輛的全狀態反饋，具有很大的實用潛力。

(2)通過分析不同SOC狀態下的換擋曲線，獲得了具有一般性的換擋規律，也在一定程度上提高了優化算法的可用性。