基于3×3核矩陣的極化碼性能分析

葉銘 李暉

摘 ?要： 為了更好地分析基于多維核矩陣的極化碼的性能，采用基于3×3核矩陣的系統極化編碼和非系統極化編碼這兩種編碼方法，做了基于3×3核矩陣的系統極化碼和非系統極化碼的性能對比實驗。仿真結果表明：基于3×3核矩陣的系統極化碼和非系統極化碼的誤幀率性能基本上是一致的;基于3×3核矩陣的系統極化碼在誤碼率性能上相對于非系統極化碼有一定幅度的提升。可見，基于3×3核矩陣的系統極化碼在性能上比非系統極化碼更具優勢。

關鍵詞： 多維核矩陣; 極化碼; 系統極化碼; 非系統極化碼; 誤幀率仿真; 誤碼率分析

中圖分類號： TN919.3?34 ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼： A ? ? ? ? ? ? ? ? ? ? ? ? 文章編號： 1004?373X（2019）09?0011?03

Performance analysis of polar codes based on 3×3 kernel matrix

YE Ming， LI Hui

（School of Information Science and Technology， Hainan University， Haikou 570228， China）

Abstract： In order to analyze the performance of polar codes based on multi?dimensional kernel matrix efficiently， the systematic polar coding method and non?systematic polar coding method based on 3×3 kernel matrix are adopted， and the performance contrast experiments of systematic polar codes （SPCs） and non?systematic polar codes （NSPCs） based on 3×3 kernel matrix are performed. The simulation results demonstrate that the frame error rate （FER） performance of SPCs and NSPCs based on 3×3 kernel matrix is basically consistent， and the bit error rate （BER） performance of SPCs has a certain improvement than that of NSPCs. It is concluded that the performance of SPCs based on 3×3 kernel matrix is superior to that of NSPCs based on 3×3 kernel matrix..

Keywords： multidimensional kernel matrix; polar code; systematic polar code; non?systematic polar code; frame error rate simulation; bit error rate analysis

極化編碼是一種可達二進制離散無記憶信道對稱容量的編碼構造方法[1]，標準形式的極化碼是非系統極化碼。目前主要有兩種極化碼系統編碼的方法，既可保留非系統編碼的低復雜度特性，又能顯著改善誤比特性能[2?3]。仿真結果表明，基于2×2核矩陣的系統極化碼與非系統極化碼具有相同的誤幀率性能，但系統極化碼的誤比特率性能更好。多維核矩陣構造的極化碼的合理性已被證明，這類極化碼的構造方法也被提出，極化碼的碼長更加靈活，碼長為[N=2n]形式的限制被打破[4?6]。對于任意二進制輸入離散無記憶信道[W]且其對稱容量[I（W）]小于任意碼率[R]，當碼長[N]足夠大且[β<][12]時，極化編碼連續刪除（Successive Cancellation，SC）譯碼下的譯碼誤塊率[peN，R=o（2-Nβ）]，即2×2核矩陣[G2]有指數[4][12]。當核矩陣足夠大時，研究發現該指數可任意逼近1，且越接近1極化碼的性能越好[5]。因此，研究基于[l×l]核矩陣[Gl]構造的極化碼（[l≥3]的核矩陣為多維核矩陣）具有重要意義。本文主要介紹了系統極化碼的編碼方法和基于3×3核矩陣的極化碼。同時，分析基于3×3核矩陣的系統極化碼和非系統極化碼的性能。

1 ?基于3×3核矩陣的極化碼

1.1 ?信道極化模型

對于二進制離散無記憶信道[W：x→y]，其中，[x={0，1}]表示輸入，[y]表示輸出，[W（yx）]表示轉移概率。[Z（W）]表示信道的可靠性（Bhattacharyya參數）：

碼長為[N=ln（l≥2）]的極化碼的合理性已被證明。極化碼的主要思想是信道極化，對于信道合并與信道拆分，碼長為[N=3n]的極化碼與碼長[N=2n]的極化碼的信道極化相似，其信道合并的模型如圖1所示[5，7]。

圖1 ?信道[W9]合并示意

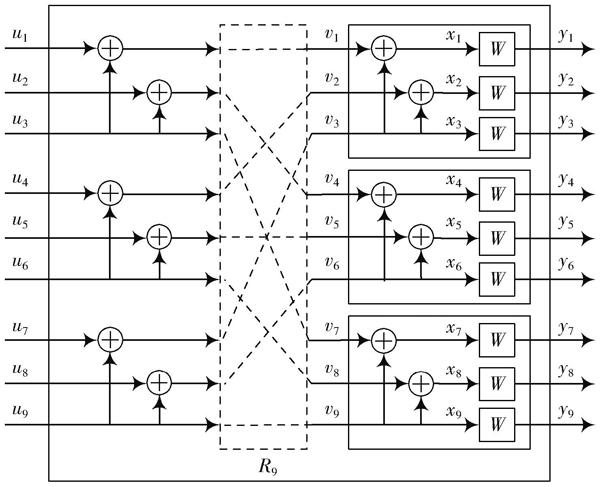
對于基于核矩陣[G2]的極化碼，在信道容量相等的情況下將信道[W]近似看成二進制刪除信道，信道[W（i）N]的可靠性可由遞歸公式（3）計算，也可通過密度進化或高斯近似的方法計算[8?9]。

1.2 ?編碼構造

基于2×2核矩陣的極化碼只有一種核矩陣，即[G2=1011]，而多維核矩陣[Gl]隨著[l]的增大擁有更多的形式，碼長為[N=ln]的極化碼在編碼構造上更靈活的同時也更難找出一個更好的核矩陣形式。例如，碼長為[N=3n]的極化碼的核矩陣[G3]就有24=16種可能形式，不同的[G3]將使構造的極化碼具有不同的性能，不同的核矩陣[G3]滿足信道極化條件的有[5]：

核矩陣[G3]后的數字如427表示[G3]每行元素對應的十進制數值，在不同的核矩陣[G3]中更好的形式為[G3]427。

2 ?系統極化碼

非系統極化碼已被系統地介紹了[1]，系統編碼的極化碼為系統極化碼。通過將[u]分成兩部分，即[u=（uA，uAc），][A?{1，2，…，N}]，用式（5）表示一類碼率可調節的碼：

[uA=（ui： i∈A）]包含在每一輪傳輸中可自由變動的用戶數據，而[uAc=（ui：i∈Ac）]包含的是在傳輸開始階段就已固定并為譯碼器已知的信息。式（5）可修改為：

式中：[GA]和[GAc]是矩陣[G]的子矩陣，分別包含[A]和[Ac]指定的行。式（6）表示非系統極化碼的編碼，其中，[uAcGAc]是固定向量;碼率[R]可通過改變集合[A]的大小調節。為了將非系統極化碼轉換成各種可能的系統極化碼，令碼字[x]分成兩部分，即[x=xB+xBc]，其中[B]是[{1，2，…，N}]的任意子集，那么式（6）可改寫為式（7）和式（8）：

式中：[GAB]表示[G]的子矩陣，包含的元素是[（Gi，j），][i∈A，j∈B]。所謂的系統極化碼編碼就是設法讓[xB]發揮和[uA]在非系統編碼中攜帶用戶數據一樣的作用。對于給定的參數為[（A，uAc）]的非系統極化碼編碼，若式（6）和式（7）中的集合[uA]和[xB]的數值存在一一對應的關系，則存在參數為[（B，uAc）]的系統極化碼編碼[2]。相似地，若集合[A]和[B]有相同的元素數目且[GAB]為可逆矩陣，參數為[（A，uAc）]的非系統編碼定義的極化碼可轉換為編碼參數為[（B，uAc）]的系統極化碼[2]。事實上，通過計算式（7）得：

此外，極化碼系統編碼的另一種方法是將連續刪除（Successive Cancellation，SC）譯碼器作為編碼器[2?3]。具體地，在二進制刪除信道上發送碼字[x]，那么用戶數據部分[xA]被完整地接收而其余部分則被刪除。

3 ?性能分析

在加性高斯白噪聲信道下對碼長為243的極化碼進行仿真實驗。對于系統極化碼和非系統極化碼，使用相同的連續刪除列表（Successive Cancellation List，SCL）譯碼器[10?12]。為了逼近極化碼的最大似然性能，譯碼器的列表大小[L]設為32。調制方式為BPSK。對于非系統極化碼，譯碼器產生一個碼字源[u]的估計[u]后就停止工作。通過比較[u]和估計[u]，對誤幀率和誤碼率統計數據進行編譯。對于系統極化碼，譯碼器在產生估計[u]后還要計算[x]的估計[x]，并且輸出[xA]。誤幀率和誤碼率統計數據通過比較[xA]和估計[xA]進行編譯[2]。

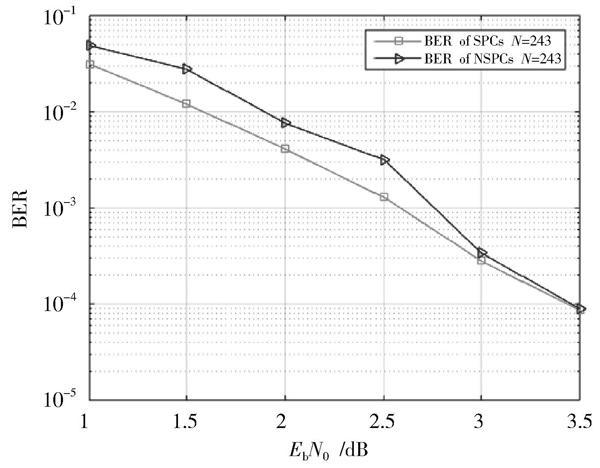
圖2給出了基于3×3核矩陣的極化碼的誤幀率性能曲線。基于3×3核矩陣的系統極化碼和非系統極化碼的誤幀率性能雖然有一些很小的差距，但基本上是一致的。通過觀察圖3發現，基于3×3核矩陣的系統極化碼與基于3×3核矩陣的非系統極化碼相比，具有較好的誤碼率性能。因此，可以認定3×3核矩陣的系統極化碼和非系統極化碼具有相同的誤幀率性能，前者的誤碼率性能要優于后者。這與基于2×2核矩陣的極化碼得出的結論是一樣的。其余多維核矩陣構造的系統極化碼和非系統極化碼的性能尚待研究，基于多維核矩陣的極化碼的構造理論和譯碼算法也是未來研究的主要課題。

圖2 ?基于3×3核矩陣的系統極化碼和非系統極化碼的誤幀率

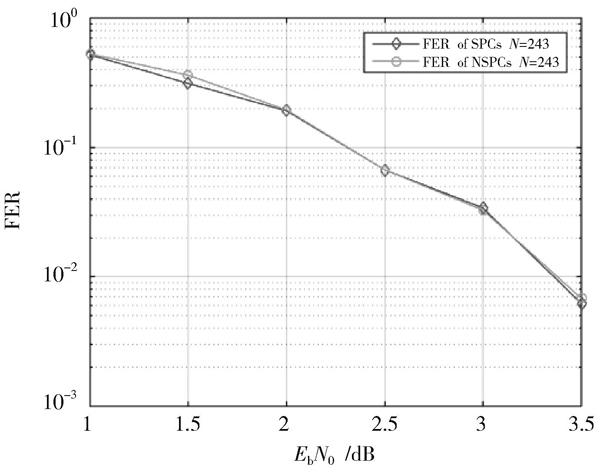
圖3 ?基于3×3核矩陣的系統極化碼和非系統極化碼的誤碼率

4 ?結 ?論

基于3[×]3核矩陣的極化碼的出現，打破了標準形式的極化碼在碼長上的限制。多維核矩陣構造的極化碼的編碼構造更加復雜，其碼長類型和核矩陣形式也靈活多樣。仿真結果表明，與標準形式的極化碼一樣，基于3×3核矩陣的系統極化碼在誤碼率性能上比非系統極化碼更具優勢，同時它們具有相同的誤幀率性能。

參考文獻

[1] TAL I. How to construct polar codes [J]. IEEE transactions on information theory， 2013， 59（10）： 6562?6582.

[2] ARIKAN E. Systematic polar codes [J]. IEEE communications letters， 2011， 15（8）： 860?862.

[3] LIU Zhenzhen， CHEN Kai， NIU Kai， et al. Distance spectrum analysis of polar codes [C]// 2014 IEEE Wireless Communications and Networking Conference. Istanbul： IEEE， 2014： 490?495.

[4] BENAMMAR M， BIOGLIO V， GABRY F， et al. Multi?kernel polar codes： Proof of polarization and error exponents [C]//Proceedings of 2017 IEEE Information Theory Workshop （ITW）. Kaohsiung， Taiwan， China： IEEE， 2017： 101?105.

[5] ZHANG Liang， ZHANG Zhaoyang， WANG Xianbin. Polar code with block?length N=3n [C]// 2012 IEEE International Confe?rence on Wireless Communications Signal Processing. Huangshan， China： IEEE， 2012： 1?6.

[6] KORADA S B， SASOGLU E， URNAKE R. Polar codes： cha?racterization of exponent of exponent， bounds， and construction [J]. IEEE transactions on information theory， 2010， 56（12）： 6253?6264.

[7] PRESMAN N， SHAPIRA O， LISYN S. Polar codes with ?mixed kernels [C]// 2011 IEEE International Symposium on Information Theory. St. Petersburg： IEEE， 2011： 1?16.

[8] TRIFONOV P. Efficient design and decoding of polar codes [J]. IEEE transactions on communications， 2012， 60（11）： 3221?3227.

[9] MORI R， TANAKA T. Performance of polar codes with the construction using density evolution [J]. IEEE communications letters， 2010， 13（7）： 6253?6264.

[10] CHEN Kai， NIU Kai， LIN Jiaru. Improvement successive cancellation decoding of polar codes [J]. IEEE transactions on communications， 2013， 61（8）： 3100?3107.

[11] CHEN Kai， NIU Kai， LIN Jiaru. List successive cancellation decoding of polar codes [J]. Electronics letters， 2012， 48（9）： 500?501.

[12] BALATSOUKAS?STIMMING A， BASTANI PARIZI M， BURG A. LLR?based successive cancellation list decoding of polar codes [C]// Proceedings of 2014 IEEE International Confe?rence on Acoustics， Speech and Signal Processing. Florence， Italy： IEEE， 2014： 3903?3907.