OFDMA系統降低PAPR的DCTACE算法
梁燕楠 李艷萍 韓碩
摘 ?要: 針對正交頻分多址(OFDMA)系統的高PAPR問題,提出一種離散余弦變換(DCT)和動態星座擴展(ACE)的聯合算法。首先對調制信號在頻域進行DCT變換,從而降低大峰值信號出現的概率。對信號做星座擴展,通過改變星座點位置,減少信號同相的概率,以此降低OFDMA系統的PAPR。在16QAM的OFDMA信號模型下對新算法PAPR、計算復雜度和誤碼率(BER)進行仿真分析,與DCT算法、ACE算法和一些改進算法相比,所提算法在不增加復雜度的前提下,具有更強的PAPR抑制能力,且基本不會降低BER性能。
關鍵詞: 正交頻分多址系統; 峰均功率比降低; 離散余弦變換; 星座擴展; 性能仿真; 誤碼率分析
中圖分類號: TN914?34 ? ? ? ? ? ? ? ? ? ? ? ? 文獻標識碼: A ? ? ? ? ? ? ? ? ? ? ? ? ?文章編號: 1004?373X(2019)09?0014?04
DCT?ACE algorithm for PAPR reduction in OFDMA system
LIANG Yannan, LI Yanping, HAN Shuo
(College of Information Engineering, Taiyuan University of Technology, Taiyuan 030024, China)
Abstract: A joint algorithm of discrete cosine transform (DCT) and convex set?mapped active constellation expansion (ACE) is proposed to reduce the PAPR (peak?to?average power ratio) of OFDMA (orthogonal frequency?division multiple access) system. The DCT is carried out for the modulated signal in the frequency domain to reduce the occurrence probability of high peak signal, and then constellation expansion is performed for the signal to reduce the in?phase probability of signal by changing the positions of constellation points, by which the PAPR of OFDMA system is reduced. The PAPR, computational complexity and bit error rate (BER) of the new algorithm are simulated and analyzed by using the 16QAM OFDMA signal model. In comparison with the DCT algorithm, ACE algorithm and other improved algorithms, the proposed algorithm has higher PAPR suppression ability and can remain the BER performance without increasing the complexity.
Keywords: OFDMA system; PAPR reduction; discrete cosine transform; constellation expansion; performance simulation; bit error rate analysis
0 ?引 ?言
近些年,無線技術的高傳輸速率和高速寬帶的應用要求一直在增加。第三代合作項目(3GPP)改進了長期演進系統(LTE),LTE引入了具有高速和高通信能力的數據速率系統。3GPP LTE在上行鏈路中使用單載波頻分多址(SC?FDMA)技術,在下行鏈路中使用正交頻分多址(OFDMA)[1]技術。OFDMA系統具有很大的傳輸數據速率、有效的頻譜利用率、頻率分集、吞吐量最大化以及針對信道失真和多徑衰落信道較好的抗擾度能力等方面的優點,比SC?FDMA更受關注;但它也有較嚴重的問題,如傳輸信號的高峰均功率比(PAPR)。高PAPR會增加功率放大器的功耗,造成帶外輻射、帶內失真和頻譜擴展[2]。PAPR問題阻礙了OFDMA系統成為通信系統下行鏈路中的無線標準[3],因此,越來越多人對PAPR問題提出了解決方案,文獻中介紹了很多OFDM系統降低PAPR的方法,其中包括信號預畸變技術[4?6]、概率類方法[7?8]和編碼類方法[9?10],一般來說,PAPR的降低是以增加復雜度或犧牲誤碼率為代價。
本文提出的算法是基于動態星座擴展(ACE)和離散余弦變換(DCT)的聯合算法,在增加較小的計算量的基礎上最大程度地降低OFDMA系統的PAPR,并能保持很好的誤碼率(BER)性能。改進算法對OFDMA信號在時域、頻域都進行了處理,DCT降低了OFDMA系統中大峰值信號出現的概率,通過頻域處理降低其PAPR。ACE技術通過對信號時域、頻域的迭代處理,適當擴大傳輸信號的星座圖,改變傳輸信號的幅度和相位,避免子載波相位調制一致的情況,進而有效降低PAPR。另外,改進算法不需要任何復雜的優化技術,降低了系統實現的復雜度。仿真結果表明,與原始算法及文中其他算法相比,本文所提算法有更強的PAPR抑制能力、較低的計算復雜度和較好的BER性能。
1 ?OFDMA系統模型及PAPR定義
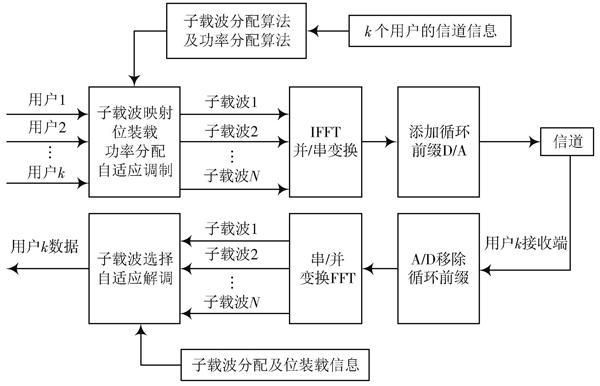
OFDMA系統是OFDM系統在多用戶環境下的應用。OFDM可以與傳統的靜態多址接入方式,如FDMA,TDMA等結合形成OFDM?FDMA,OFDM?TDMA等靜態的多用戶資源分配方式。系統框圖如圖1所示。
圖1 ?OFDMA系統框圖

用[N]個不同的子載波傳輸OFDMA信號,令[X={Xk,k=0,1,2,…,N-1}]表示OFDMA信號的[N]個符號,選擇[N]個正交化的子載波[{fk,k=0,1,2,…,N-1}]用于傳輸[N]個OFDMA符號,其中,[fk=kΔf,Δf=1(NT)],[T]為原始信號的周期,取過采樣因子[L],離散OFDMA信號可寫為:
2 ?PAPR降低算法
2.1 ?DCT
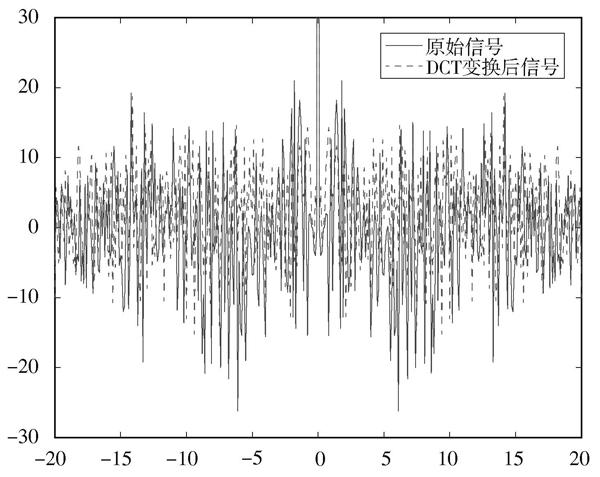
與Hadamard變換方法相似,DCT變換也是具有良好邊帶特性的正交變換。為了降低OFDMA信號的PAPR,輸入信號在進入IFFT模塊前先經過DCT變換減小大峰值信號出現的概率。圖2為原始信號和經過DCT變換后信號的仿真曲線圖,可以看出,DCT變換后,信號相對較平穩,出現大峰值信號的概率降低。
圖2 ?DCT變換前后信號曲線圖

通過DCT變換,降低大峰值信號出現的概率,從而降低式(2)中的分子,有效降低OFDMA信號的PAPR。
2.2 ?ACE
ACE方法要求對時域和頻域信號處理, 在這種方法中,時域信號首先進行限幅濾波操作,產生的噪聲會造成星座點的移動。每個符號的延伸必須在允許區域內,否則回到原始位置。通過迭代循環執行這些過程以實現PAPR的優化。ACE算法的目的是改變星座點的位置,減少OFDMA信號同相的概率,以此降低PAPR。
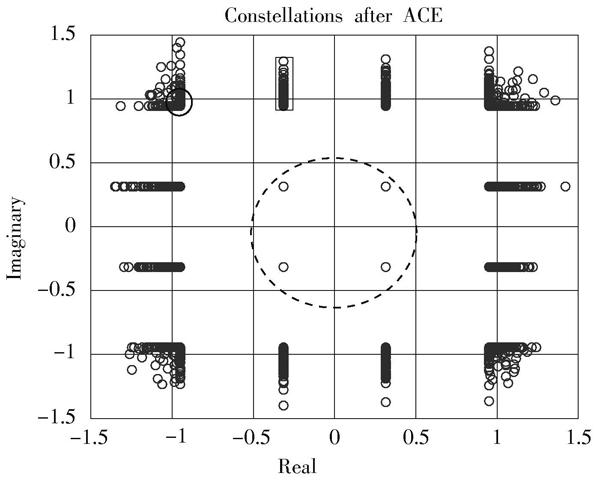
如圖3所示,ACE允許拐角(實線圓圈)QAM星座點在其標稱值之外的[14]平面內移動,為了保持星座符號之間的最小距離,內部點(虛線圓圈)不被調整,對于其他邊界點(黑色矩形)中的點,可轉移的范圍指向星座的外部。
圖3 ?16QAM星座擴展圖

ACE技術的主要優點在于降低PAPR時不會損失數據速率。此外,在恢復發送數據時,接收機不需要邊帶信息。
2.3 ?改進算法
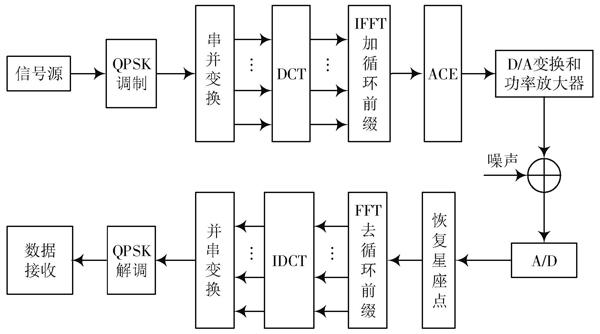
為了減少OFDMA系統的PAPR,提出一種DCT聯合ACE的算法,算法原理圖如圖4所示。
圖4 ?算法原理圖
算法的具體步驟如下:
1) 輸入序列首先經過QPSK調制后做DCT變換:
2) [X]經過IFFT模塊得到對應的[x];
3) 對[x[n]]做如下處理:
4) 對[x]做FFT得到[X];
5) 對[X]做ACE條件約束,滿足條件的保留,否則置零;
6) 將約束后的[X]做IFFT變換,則星座擴展后的時域信號為[x];
7) 返回步驟1)直到達到最大迭代次數,測量PAPR是否基本最小化。
2.4 ?復雜度分析
由于DCT變換矩陣為正交陣,所以可以忽略DCT變換的計算量,只考慮ACE的計算復雜度。ACE算法的計算復雜度與迭代次數[I]密切相關,所需的復數乘和復數加分別為[I×(2N+N2log2N)]和[I×(4N+Nlog2N)] 。在計算量基本沒有改變的前提下,本文算法對PAPR的抑制能力更強,收斂速度更快。
3 ?仿真結果與分析
本節對所提算法的綜合性能進行仿真驗證,仿真參數設置如下:OFDMA系統采用16QAM調制,符號數為10 000,子載波數[N=]256,過采樣倍數[L=4],迭代門限值為6 dB,DCT維數為256。另外,為便于比較,本文給出了一些其他算法的仿真性能曲線。
圖5顯示了DCT?ACE算法在不同條件下降低PAPR的CCDF性能,比較了子載波數為[N=256]和[N=128]時的PAPR抑制能力,由曲線可知,子載波數較小時,可以忽略子載波數對PAPR性能的影響。[N=256]時,在CCDF=[10-3]處,不同迭代次數下相較于原始信號分別優化了3 dB,4.1 dB,4.7 dB,PAPR的抑制效果較好。
圖6給出了DCT?ACE算法與DCT的其他聯合算法的比較,由圖中曲線可知,DCT?SLM較好地抑制了PAPR,在CCDF=[10-3]處,比DCT?ACE一次迭代算法優化了0.7 dB。在DCT?ACE算法進行二次和三次迭代時,PAPR性能比DCT?SLM算法優化了0.4 dB和1 dB,而且本文算法的計算復雜度遠遠低于DCT?SLM算法。由前人的研究表明,壓擴算法有很強的PAPR抑制能力。設置壓擴參數為2,對DCT?Companding仿真,改進算法三次迭代下比DCT?Companding算法優化了0.7 dB。雖然計算量較大,但不會造成誤碼率的損失。由此可以看出,新算法相對來說有著較快的收斂速度,PAPR抑制能力強,綜合性能較好。
圖5 ?不同子載波下DCT?ACE的CCDF曲線
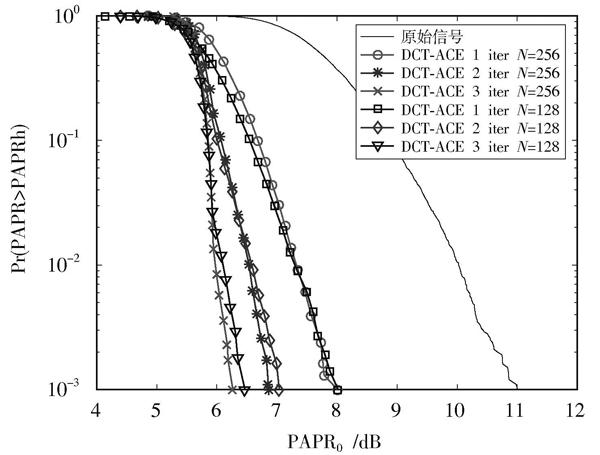
圖6 ?DCT聯合不同算法的CCDF曲線
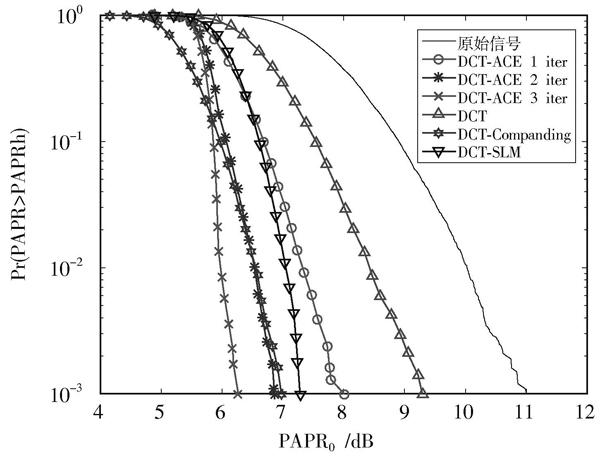
圖7給出了DCT?ACE算法與ACE算法及ACE?Hadamard算法的CCDF曲線圖。由圖中曲線可知,DCT?ACE算法比其他算法有更好的PAPR抑制能力。在CCDF=[10-3]處,DCT?ACE算法與ACE?Hadamard聯合算法相比,雖然一次迭代性能差,但是三次迭代優化了0.7 dB;與ACE 3 iter相比,DCT?ACE算法一次、二次、三次迭代分別優化了1.1 dB,2.2 dB和2.9 dB。所以,本文算法比其他算法有更快的收斂速度,總體性能較好。
圖7 ?ACE聯合不同算法的CCDF曲線

圖8給出了原始ACE和DCT以及所提聯合算法經過高斯白噪聲信道后的BER特性曲線。由圖中曲線可以看出,單獨采用DCT變換,不會造成誤碼率的損失,單獨采用ACE三次迭代算法,會帶來一定程度的誤碼率損失,DCT?ACE算法提高了誤碼率性能,在[BER=10-2]處,新算法的誤碼率比原始ACE算法優化了約0.003 dB。所以,新算法不僅有較好的PAPR抑制能力,誤碼性能也得到提高。
圖8 ?BER性能曲線

4 ?結 ?論
針對OFDMA系統中PAPR較高的問題,基于原始ACE算法和DCT算法對PAPR抑制能力較弱的仿真事實,提出聯合DCT和ACE的改進算法降低OFDMA系統PAPR的方案。使用Matlab仿真驗證了算法的可行性,與原始ACE和DCT算法以及參考文獻中的某些改進算法相比,本文算法不僅能較大程度地降低OFDMA系統PAPR,且保證了誤碼率性能。綜合考慮計算復雜度、PAPR抑制能力和誤碼率特性,本文算法具有很大實用性。
參考文獻
[1] MYUNG H G, LIM J, GOODMAN D. Single carrier FDMA for uplink wireless transmission [J]. IEEE vehicular technology magazine, 2006, 1(3): 30?38.
[2] ZHUANG Ling, LIU Lu, LI Jibi, et al. Discrete sine and cosine transforms in single carrier modulation systems [J]. Wireless personal communications, 2014, 78(2): 1313?1329.
[3] RAHMATALLAH Y, MOHAN S. Peak?to?average power ratio reduction in OFDM system: a survey and taxonomy [J]. IEEE communications surveys & tutorials, 2013, 15(4): 1567?1592.
[4] HAO M J, LAI C H. Precoding for PAPR reduction of OFDM signals with minimum error probability [J]. IEEE transactions on broadcasting, 2010, 56(1): 120?128.
[5] JORGE F S, DANIEL R, ROBERTO L V. Active interference cancellation for OFDM spectrum sculpting: linear processing is optimal [J]. IEEE communications letters, 2014, 18(9): 1543?1546.
[6] WANG Zhongpeng. Combined DCT and companding for PAPR reduction in OFDM signals [J]. Journal of signal & information processing, 2011, 2(2): 100?104.
[7] 張博葉,李艷萍,耿曉文.降低MIMO?OFDM系統峰均比的QAP算法研究[J].現代電子技術,2017,40(5):19?21.
ZHANG Boye, LI Yanping, GENG Xiaowen. Research on QAP algorithm for PAPR reduction of MIMO?OFDM system [J]. Modern electronics technique, 2017, 40(5): 19?21.
[8] ABOUTY S, LI R, ZENG F. New SLM technique with low complexity based on matrices combined with DCT transform for PAPR reduction in OFDM communication systems [J]. Journal of convergence information technology, 2012, 7(17): 232?242.
[9] KANG Ce, LIU Yi, HU Meixia, et al. A low complexity PAPR reduction method based on FWFT and PEC for OFDM systems [J]. IEEE transactions on broadcasting, 2017, 63(2): 416?425.
[10] XU Renhui, WANG Lei. A unitary precoder for optimizing spectrum and PAPR characteristic of OFDMA signal [J]. IEEE transactions on broadcasting, 2018, 64(2): 293?306.

