移相全橋魯棒性變增益控制策略的研究
宗振祥 廖冬初 蔡華鋒 孟文靖

摘 ?要: 針對傳統PID控制的移相全橋變換器難以獲得理想的動靜態特性,在分析移相全橋模型的基礎上,設計以輸入電壓和負載作為變參數的線性變參數模型。利用變參數極值組合將其變為多胞形模型,并通過對其頂點進行穩定性分析和控制器設計,得到一種建立在軟開關移相全橋變換器的多胞形線性變參數模型基礎上的魯棒性變增益調度控制。通過Matlab仿真與傳統的PID控制進行比較,表明魯棒性變增益控制器具有更好的控制效果。
關鍵詞: 移相全橋; PID; 變換器; 線性變參數; 魯棒性變增益控制; 多胞形
中圖分類號: TN876?34; TM28 ? ? ? ? ? ? ? ? ? 文獻標識碼: A ? ? ? ? ? ? ? ? ? ? ?文章編號: 1004?373X(2019)09?0081?05
Research on robust variable gain control strategy for phase?shifted full?bridge converter
ZONG Zhenxiang1, LIAO Dongchu1, 2, CAI Huafeng1, 2, MENG Wenjing3
(1. School of Electrical and Electronic Engineering, Hubei University of Technology, Wuhan 430068, China;
2. Hubei Collaborative Innovation Center for High?efficiency Utilization of Solar Energy, Hubei University of Technology, Wuhan 430068, China;
3. Hebi Power Company, State Grid Henan Electric Power Company, Hebi 458000, China)
Abstract: Since the phase?shifted full?bridge (PSFB) converter controlled by traditional PID is difficult to obtain the desired dynamic and static characteristics, the linear parameter varying (LPV) model taking input voltage and load as variable parameters is designed on the basis of PSFB model, and transformed into the polytope model by means of variable parameter extreme values combination. The stability analysis and controller design are carried out for the vertex of the polytope model to obtain a robust variable gain scheduling control based on the polytope linear parameter varying model of soft?switching PSFB converter. The control strategy is compared with traditional PID control strategy with Matlab simulation. The result shows that the robust variable gain controller has better control effect.
Keywords: phase?shifted full?bridge; PID; converter; linear parameter varying; robust variable gain control; polytope
0 ?引 ?言
DC/DC變換器中常用的拓撲結構為移相全橋,該電路對功率器件應力要求低,在高頻變壓器利用率較高的同時,保證前后級完全的電氣隔離,再加上軟開關在移相全橋中的應用,使得移相全橋在使用較多功率器件的同時保持較高的效率,所以在中大功率場合中應用極為廣泛。作為閉環的自動控制系統,工業中常用的控制方法為PID控制,其優點為結構簡單、控制方便,PID控制器對線性系統控制效果優異,但移相全橋變換器是一個非線性時延的系統,文獻[1]提出的線性控制方式理論上只能在特定的工作點附近具有較好的控制性能,研究了移相全橋DC/DC變換器當輸入電壓、負載功率、開關頻率、變壓器原邊等效諧振電感變化時對系統穩定性和動靜態性能的影響。除此之外,器件的差異與老化都會導致與設計的數學模型產生偏差,影響移相全橋變換器輸出特性的惡化。近年來魯棒性控制的發展推動了LPV(線性變參數)控制的發展,文獻[2]詳細地研究了從LPV系統建模到基于LPV模型的魯棒性變增益控制器的設計方法。本文針對輸入電壓變化與負載變化對移相全橋電路的影響,建立以輸入電壓和負載為變參數的ZVSPSFB(軟開關移相全橋)的LPV模型,設計魯棒性變增益控制器。該控制器可以增強系統對外部擾動與內在參數變化的魯棒性。最后在Matlab中進行模型搭建,通過仿真驗證該控制器的可行性,與傳統的PID控制器進行比較,可知該控制方法響應速度更快,靜態誤差更小,輸入電壓與負載變化時對系統性能影響更小。
1 ?ZVSPSFB結構及模型建立
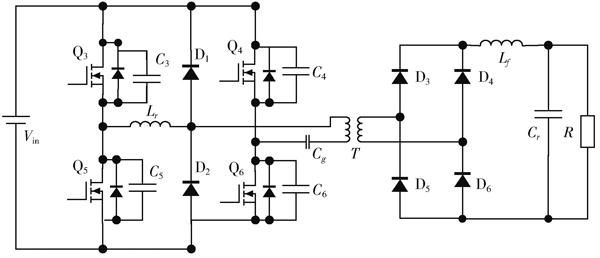
本文研究的軟開關移相全橋的主電路拓撲結構如圖1所示。
圖1 ?軟開關移相全橋變換器拓撲結構

移相全橋變換器雖然采用的是全橋結構,但是其本身產生的效果與Buck變換器中使用開關管的效果是一致的,它們都是靠控制開關管的開通和關斷達到對輸出電壓進行控制的目的。
電力電子變換器的線性模型對系統的變化十分敏感,負載與器件的參數不確定性對系統的響應有潛在的威脅,所以在控制器的設計過程中,考慮參數的不確定性具有研究意義。本文引進凸多面體表現移相全橋變換器的不確定性,移相全橋等效原理圖[3?4]如圖2所示。
圖2 ?移相全橋等效原理圖

在系統進行建模之前,假設系統工作在CCM(電感電流連續)模式下,各器件均為理想元件,其中[L]和[C]是輸出濾波電感和電容,[R]為負載,S為開關管。基于圖2的簡化模型,在S開通和關斷情況下,根據基爾霍夫電壓和電流定律:
式中:電流擾動為[ird];[Vin]和[Vo]表示輸入和輸出電壓;[n]為變壓器變比;[u]表示控制器輸出。狀態矩陣中某些元素可能是不確定或者時變的,那么狀態矩陣中取決于一些不確定或者時變的項,這樣可以將式(3)表示成帶有參數的函數:
移相全橋的LPV模型就建模完成了,接下來要針對移相全橋變換器的LPV模型設計狀態反饋魯棒性變增益控制器。
2 ?魯棒性變增益控制器設計
傳統增益調度控制方法依賴對非線性系統多工作點的選取與各控制器之間的切換,需要大量仿真,缺乏理論支持。魯棒性變增益控制可以直接設計一個連續變換的控制器,并且可以從理論驗證其穩定性,變參數的連續性又會增加計算量,考慮利用多胞形LPV系統的頂點性質[5]。多胞形LPV系統只需對頂點進行設計,頂點內部參數均滿足控制要求。
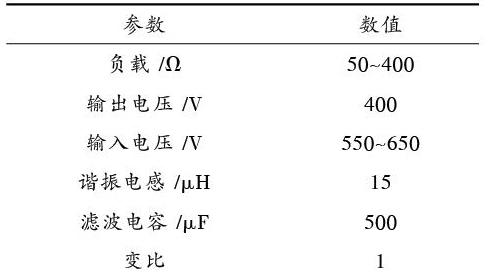
針對式(7)移相全橋變換器的凸多面體LPV模型,根據4個頂點分別設計狀態反饋增益[K1],[K2],[K3]和[K4],利用LMI技術把魯棒性變增益控制問題轉化為凸優化問題,根據[D]域穩定性定理,使閉環極點落在復數左半域圓心在[(-q,0)],半徑為[r(r [K=ρ1θK1+ρ2θK2+ρ3θK3+ρ4θK4] (9) 本文介紹一個定理,以保證最小的[H∞]范數[γ][6]。 定理1 ?對于線性時不變系統: 那么系統式(10)是可穩定的,并且這樣的狀態反饋控制器[K=LX-1],關于定理1的證明,通過有界實引理,很容易就可以得出。結合LMI 將系統的極點配置到圓盤區域,根據[D]域穩定性定理,結合式(11),取正定矩陣[X]與式(11)中的矩陣[X]相等,可以得出以下定理: 定理2 ?對于式(10)所示的線性時不變系統,給定的[γ>0],存在正定對稱矩陣[X]和[L=KX],滿足如下不等式約束: 式中[Pt=P1t,P2t,…,Pnt],其中,[Pi≤][Pit≤Pi]是系統物理參數的時變參數序列。對于凸多胞系統式(14)來說,根據定理2,對其各個頂點[SΠi]設計滿足性能要求的反饋增益之后,利用式(9)的凸多胞形LPV控制器可獲得處在任意位置[θ]的反饋控制[K]。在這之前的分析,都是給定[H∞]性能[γ],這樣的控制器稱為[γ?]次優化[H∞]控制器。但是在本文中所要設計的多胞形系統是具有[H∞]最優控制器,即對所有的[γ]進行搜索,得到使閉環系統具有擾動抑制度[γ]最小化的控制器。所以,對于多胞形系統來說,通過狀態反饋[u=Kx],如果存在一個對稱的矩陣[X]和矩陣[Li=KiX],使得以下不等式約束成立: 如果上述各頂點處的優化問題有解,那么狀態反饋增益[Ki=LiX-1]不僅可以保證閉環的極點落在圓盤域[L(q,r)]中,而且可以保證閉環的擾動抑制具有最小的[H∞]性能[γ]。基于狀態反饋的凸多胞形結構系統的LPV控制器為: 3 ?仿真驗證 本節針對建立的軟開關移相全橋電路進行Simulink仿真,并與相應的PID控制器的結果進行比較,軟開關移相全橋電路參數如表1所示。表1 ?軟開關移相全橋電路參數

圖3 ?輸出電壓響應
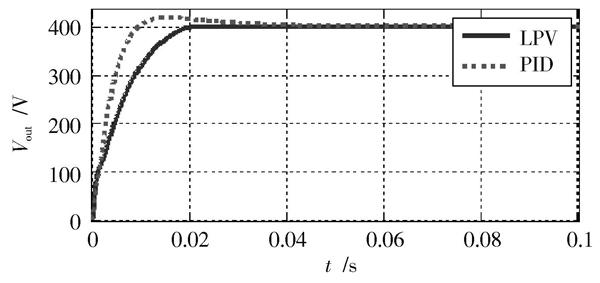
與傳統PID控制相比,LPV魯棒性變增益控制輸出在20 ms,而常規PID控制則存在超調且在40 ms時穩定,可以體現出基于LPV模型的魯棒性變增益控制下的軟開關移相全橋響應迅速且無超調。將兩種控制方法的輸出電壓穩態誤差進行比較,如圖4所示。
圖4 ?穩態誤差
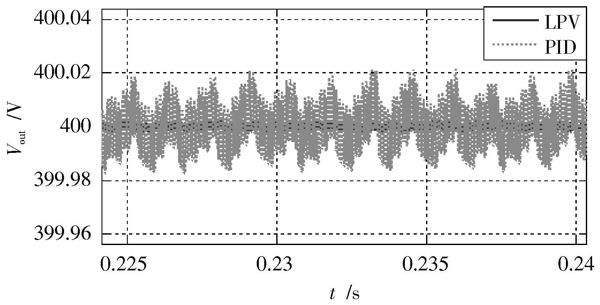
通過比較可知,LPV控制方法的控制精度比傳統PID控制的精度高,控制精度高達0.003 8 V紋波以內,是傳統PID控制精度0.038 V的[110]。將輸入電壓穩定在590 V,在0.15 s時將輸出電壓增加到650 V,觀察兩種控制方法的輸出電壓響應波形變化,如圖5所示。
圖5 ?輸入電壓突變時的輸出電壓響應
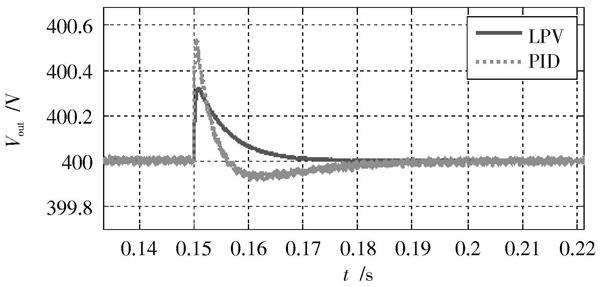
在0.15 s輸入電壓發生突變時,PID控制出現0.52 V的紋波且調節過程中出現超調,最終0.18 s時使輸出電壓穩定在400 V;而LPV魯棒性變增益控制在出現電壓突變的時刻,出現0.33 V的電壓變化,且在0.17 s時使輸出電壓穩定在400 V。可以體現出LPV控制器的系統超調小,調節迅速,過渡平滑。
在輸入為600 V,負載為100 Ω的條件下,在0.25 s時刻使負載從100 Ω變為50 Ω,兩種控制器的輸出電壓響應如圖6所示。
圖6 ?負載突變時的輸出電壓響應
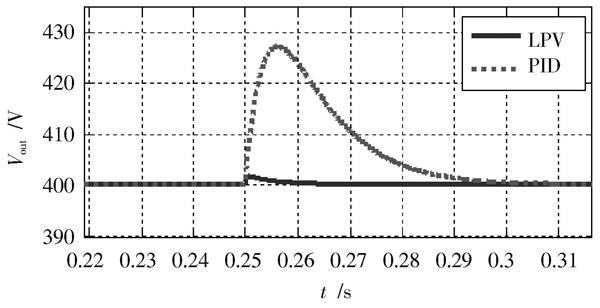
從圖6可以看出,在0.25 s時系統負載由100 Ω突變到50 Ω,LPV魯棒性變增益控制的輸出電壓紋波為1.665 V,遠遠小于傳統PID控制下的負載突變時的紋波。并且魯棒性變增益控制器的調節時間為20 ms,遠小于PID控制下的50 ms的調節時間,所以LPV模型下變增益控制器在負載突變時的系統響應與傳統PID控制相比,紋波小,響應時間快。
4 ?結 ?論
本文以輸入電壓與負載為系統的變參數,建立以兩個參數的極值組合構成的凸多面體結構的LPV模型。利用多胞形LPV系統的頂點性質,只需計算頂點的增益,計算量小,容易實現。通過與傳統PID控制器進行對比,突出基于LPV模型魯棒性變增益控制的優勢,響應較為迅速且無超調,輸出靜差小,在輸入電壓與負載電阻變化時,具有輸出電壓變化小,且調節迅速的優點,具有一定的研究價值。
參考文獻
[1] 金浩.移相全橋DC/DC變換器控制策略的研究[D].武漢:華中科技大學,2015.
JIN Hao. Research on the control strategy of phase?shifted full bridge DC/DC converter [D]. Wuhan: Huazhong University of Science and Technology, 2015.
[2] 李文強.LPV魯棒性變增益控制研究及其應用[D].北京:國防科學技術大學,2009.
LI Wenqiang. Research and application of robust gain?schedu?ling based on LPV system [D]. Beijing: ?National University of Defense Technology, 2009.
[3] GENG Jianhua, ZHANG Changfan, LUO Cheng. Research of a PWM?based new sliding?mode controller for the BUCK conver?ter [C]// 2007 the 2nd IEEE Conference on Industrial Electro?nics and Applications. Harbin: IEEE, 2007: 1907?1911.
[4] OLALLA C, LEYVA R, EIAROUDI A. et al. Robust LQR control for PWM converters: an LMI approach [J]. IEEE transactions on industrial electronics, 2009, 56: 2548?2558.
[5] CHEN C C, CHEN C L, CHANG J X, et al. LPV gain?scheduling control for a phase?shifted PWM full?bridge soft switched converter [C]// The 19th World Congress on International Federation of Automatic Control. Cape Town: IFAC, 2014: 6135?6140.
[6] 俞立.魯棒控制?線性矩陣不等式處理方法[M].北京:清華大學出版社,2002.
YU Li. Robust control?linear matrix inequality processing method [M]. Beijing: Tsinghua University Press, 2002.
[7] 殷明,陸宇平,何真.變體飛行器LPV建模與魯棒增益調度控制[J].南京航空航天大學學報,2013,45(2):202?208.
YIN Ming, LU Yuping, HE Zhen. LPV modeling and robust gain scheduling control of morphing aircraft [J]. Journal of Nanjing University of Aeronautics & Astronautics, 2013, 45(2): 202?208.
[8] 林蔭宇,張金奎,劉洋溢,等.移相全橋零電壓PWM變換器的建模與仿真[J].重慶大學學報(自然科學版),2000,23(2):49?52.
LIN Yinyu, ZHANG Jinkui, LIU Yangyi, et al. Full bridge zero?voltage?switched PWM converter [J]. Journal of Chongqing University (Natural Science Edition), 2000, 23(2): 49?52.
[9] 阮新波.脈寬調制DC/DC全橋變換器的軟開關技術[M].2版.北京:科學出版社,2013.
RUAN Xinbo. Soft?switching technique of PWM DC/DC full?bridge converter [M]. 2nd ed. Beijing: Science Press, 2013.
[10] 胡躍明.非線性控制系統理論與應用[M].2版.北京:國防工業出版社,2005.
HU Yueming. Theory and application of nonlinear control system [M]. 2nd ed. Beijing: National Defense Industry Press, 2005.

