基于[α]階逆解耦的多變量內(nèi)模控制系統(tǒng)研究

施丹 許必熙

摘 ?要： 由于工業(yè)過程控制中存在大時滯現(xiàn)象，使得單變量內(nèi)模控制難以獲得有效的控制，而多變量內(nèi)模控制成為一種較好的控制策略。文中簡單介紹了多變量內(nèi)模控制的原理，分別基于主回路為控制對象、V規(guī)范解耦的原則和[α]階逆解耦進行內(nèi)模控制器的設計，闡述了各個控制器的主要思想及其設計的具體方法。通過仿真比較模型匹配與模型失配下的內(nèi)模控制輸出仿真圖。由仿真結(jié)果可以得出，基于V規(guī)范解耦的內(nèi)模控制器具有較好的控制效果，但是解耦效果存在缺陷，針對非線性系統(tǒng)提出的基于[α]階逆解耦的內(nèi)模控制系統(tǒng)具有較好的解耦和控制效果。

關鍵詞： 多變量; 主回路; V規(guī)范解耦; [α]階逆解耦; 內(nèi)模控制; 魯棒性

中圖分類號： TN876?34; TP391.9 ? ? ? ? ? ? ? ? ? ?文獻標識碼： A ? ? ? ? ? ? ? ? ? 文章編號： 1004?373X（2019）09?0107?04

Research on multivariable internal model control system based on

[αth?order] inverse decoupling

SHI Dan， XU Bixi

（College of Electrical Engineering and Control Science， Nanjing Tech University， Nanjing 211800， China）

Abstract： Since the single?variable internal model control is difficult to obtain the effective control due to the large time delay in the industrial process control， the multivariable internal model control can better solve the problem. The principle of multivariable internal model control is introduced briefly， and the internal model controllers are designed on the basis of the main loop taken as the control object， principle of V specification decoupling and [α]th?order inverse decoupling respectively. The main ideas of each controller and its design method are described. The output simulation charts of internal model control at model matching and model mismatching are compared with simulation. The simulation results show that the internal model controller based on V specification decoupling has better control effect， but there are some defects in decoupling effect. The internal model control based on [α]th?order inverse decoupling is proposed for nonlinear systems， and the system has perfect decoupling and control effect.

Keywords： multivariate; main loop; V specification decoupling; [αth?order] inverse decoupling; internal model control; robustness

0 ?引 ?言

如今工業(yè)過程控制中存在大時滯現(xiàn)象，使得單變量內(nèi)模控制難以應用高增益，使得系統(tǒng)響應緩慢和偏差，導致工業(yè)對象難以獲得有效的控制[1]。多變量內(nèi)模控制具有和單變量內(nèi)模控制相同的特性，該特性使多變量內(nèi)模控制成為一種較好的控制策略。文獻[2?3]提出利用V規(guī)范的內(nèi)模解耦控制器，該方法創(chuàng)造性地運用了模型逆的概念，避免了矩陣求逆的過程，使設計更加簡便。

文獻[4]針對制冷系統(tǒng)設計了采用集中逆向解耦結(jié)構的內(nèi)模控制方法，在反饋通道上加入濾波器提升制冷系統(tǒng)對負荷擾動的抗擾性，解決了其大滯后、強耦合和擾動復雜的問題。為了進一步提高系統(tǒng)的抗干擾能力，文獻[5]提出一種基于支持向量機廣義逆內(nèi)模控制的方法，增強整個系統(tǒng)的魯棒性。本文采用不同的解耦策略對系統(tǒng)進行內(nèi)模控制的研究，提出一種基于[α]階逆解耦的內(nèi)模控制系統(tǒng)的研究方法，通過仿真比較，得出系統(tǒng)具有較好的解耦和控制效果。

1 ?多變量內(nèi)模控制原理

內(nèi)模控制原理如圖1所示，[GIMC，GP，GM]分別表示控制器、多變量控制對象、對象模型的矩陣。其中，[GP=g11…g1n???gm1…gmn]，[gij=gij0e-τijs]，[gij0]嚴格正則，[τij]為非負常數(shù);當[m=n]時，控制系統(tǒng)為方型系統(tǒng)。

設[I]為[n]階單位矩陣，則根據(jù)圖1可得輸出[Y]和輸入[R]之間的閉環(huán)傳遞函數(shù)關系為：

圖1 ?多變量內(nèi)模控制原理圖

所以閉環(huán)系統(tǒng)可以解耦等同于[GPGIMC]可以解耦;同樣，如果控制對象[GP]穩(wěn)定時，那么系統(tǒng)開環(huán)穩(wěn)定，即[GIMC]穩(wěn)定。但是在設計控制器的過程中，由于模型中各元素的時滯和互聯(lián)性的影響，使得多變量內(nèi)模控制不能像單變量那樣容易得到[GP+]，這就需要對控制系統(tǒng)進行適當?shù)奶幚恚缓蟀凑諉巫兞坷碚撨M行設計[6]。

2 ?主回路為控制對象的內(nèi)模控制

在多變量內(nèi)模控制系統(tǒng)中，利用內(nèi)模控制理論所具有的抗干擾性和魯棒性以克服其他回路對主回路的耦合，將主回路中的元素按照單變量控制的方法設計，并視其他回路輸出信號。該方法適合具有不同非最小項零點及通道時滯和各通道互聯(lián)性較小的多變量系統(tǒng)。研究該方法主要為了說明內(nèi)模控制本身具有一定的解耦功能[7]。

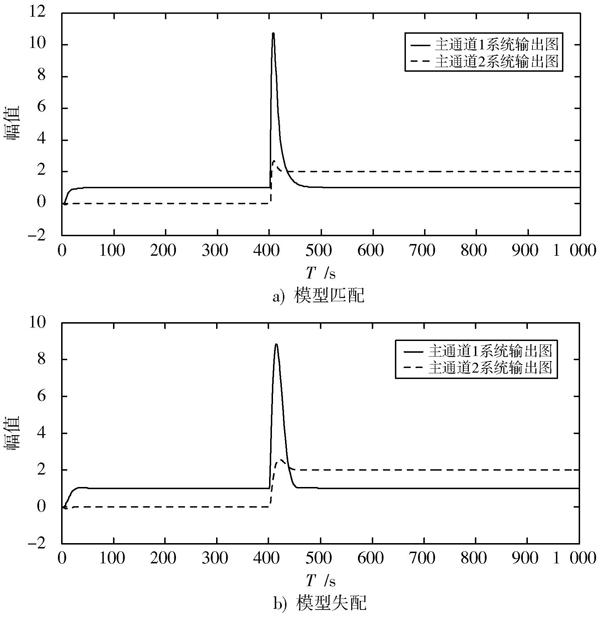
主通道1的輸入為在1 s時觸發(fā)的單位階躍信號，濾波器參數(shù)為[λ1=170]，[λ3=160];主通道2的輸入為在400 s時觸發(fā)的幅值為2的階躍信號，濾波器參數(shù)為[λ2=1]，[λ4=5]，仿真結(jié)果如圖2所示，圖2a）為模型匹配系統(tǒng)輸出圖，圖2b）為模型失配系統(tǒng)輸出圖。

圖2 ?按主回路內(nèi)模控制輸出仿真圖

從仿真圖2中可以看出，該系統(tǒng)在存在干擾或設定值變化時可能出現(xiàn)較大的波動，這對系統(tǒng)具有一定的沖擊，需要進行改進。當模型失配時，通過重新設計控制器，系統(tǒng)的輸出曲線均能夠達到設定值，分析方法與模型匹配的相同，從仿真圖2b）得到該方法對模型失配的情況具有一定的魯棒性。

3 ?V規(guī)范型多變量內(nèi)模解耦

為了體現(xiàn)上述理論方法，選擇和按主回路設計的內(nèi)模控制一樣的控制對象[8]：

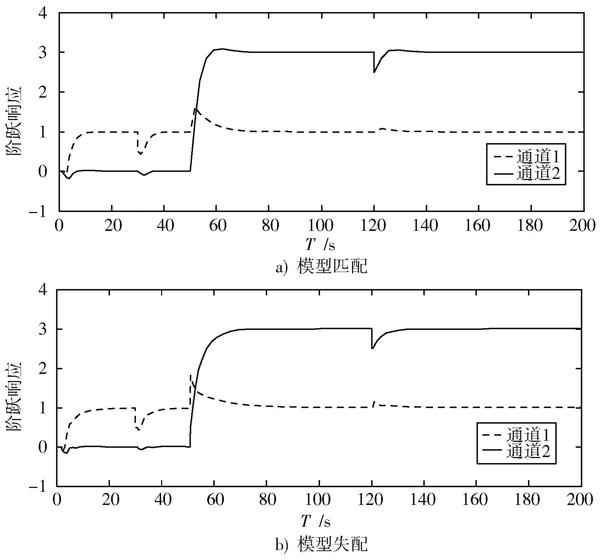
無論模型匹配或者失配，經(jīng)過V規(guī)范解耦后的內(nèi)模控制系統(tǒng)均能夠達到控制要求，如圖3所示。但在50 s時通道2的輸入信號觸發(fā)，此時對通道1存在一定的影響，解耦效果不明顯。即當一個通道出現(xiàn)干擾時，另一個通道也受到了一定的影響。

圖3 ?系統(tǒng)響應輸出曲線圖

4 ?基于[α]階逆解耦的內(nèi)模控制

所謂逆系統(tǒng)是將原系統(tǒng)的期望輸出[ydt]作為逆系統(tǒng)的輸入來產(chǎn)生原系統(tǒng)所需的控制量[udt]，以驅(qū)動原系統(tǒng)產(chǎn)生期望的輸出[ydt]。逆解耦后系統(tǒng)傳遞函數(shù)為：

4.1 ?[α]階逆解耦的多變內(nèi)模控制

基于[α]階逆系統(tǒng)解耦的內(nèi)模控制結(jié)構圖，如圖4所示。圖中[GIMC]為內(nèi)模控制器;[GP]為[n]維多輸入多輸出的原系統(tǒng);[GM]為廣義偽線性模塊;[R]表示系統(tǒng)輸入設定值;[Y]為系統(tǒng)的輸出值;[Y]為偽線性系統(tǒng)的輸出;[φ]為控制器的[α]階逆輸出信號。當存在[j=1qαj=n]時，可以省去狀態(tài)反饋[9?10]。

圖4 ?[α]階逆系統(tǒng)解耦的內(nèi)模控制系統(tǒng)

4.2 ?基于[α]階逆的內(nèi)模控制系統(tǒng)的仿真

基于[α]階逆的內(nèi)模控制系統(tǒng)選擇如下非線性控制對象。

兩通道輸入分別為：通道1在1 s處為單位階躍信號，通道2在10 s處幅值為2的階躍信號。選擇濾波參數(shù)[λ1=2，λ2=3，λ3=1，λ4=0.1]。并在通道1的干擾為：50 s觸發(fā)，幅值為0.5的階躍響應;通道2的干擾為：80 s觸發(fā)，幅值為0.5的階躍響應。仿真時間為150 s，采樣時間為1 s。控制系統(tǒng)的模型對象采用[S]?function描述，仿真結(jié)果見圖5。圖5a）為模型匹配時的系統(tǒng)輸出曲線，圖5b）為模型失配時的輸出曲線。

圖5 ?基于[α]階逆解耦的系統(tǒng)控制效果圖

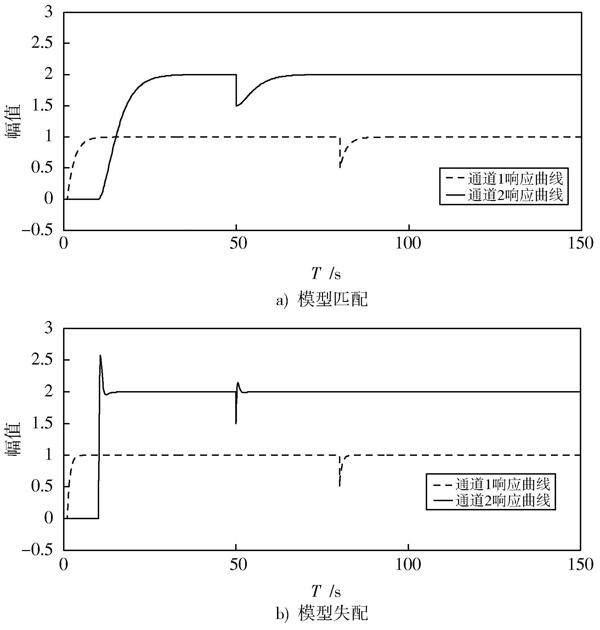
通過圖5與圖3的比較可以得出，在通道1與通道2不同時間對其加入階躍干擾后，另外的一個通道不受影響，說明進行[α]階逆解耦的效果較好，然后與內(nèi)模控制器相結(jié)合，系統(tǒng)能夠快速達到系統(tǒng)設定值且抗干擾性和魯棒性較好。但是從模型失配的圖中發(fā)現(xiàn)，無論系統(tǒng)如何調(diào)節(jié)，響應曲線均出現(xiàn)一定的超調(diào)量，但能夠快速恢復到設定值。

5 ?結(jié) ?論

本文介紹多變量內(nèi)模控制的基本原理，然后重點研究了按主通道設計的內(nèi)模控制系統(tǒng)和基于V規(guī)范解耦的多變量內(nèi)模控制，并通過舉例仿真得出基于V規(guī)范解耦的內(nèi)模控制器具有較好的控制效果，但是解耦效果存在缺陷。最后針對非線性系統(tǒng)提出基于[α]階逆解耦的內(nèi)模控制，[α]階逆解耦內(nèi)模控制是基于數(shù)學模型逆解耦控制，工業(yè)上的模型大多數(shù)都是近似等效得到，模型難以精確地獲得，因此需要采用一種有效的方法等效逆解耦模型來進一步提高控制效果。從本文的仿真對比結(jié)果來看，基于[α]階逆解耦的多變量內(nèi)模控制系統(tǒng)具有較好的解耦和控制效果。