顧及有色噪聲的自適應粒子濾波UWB定位算法

張 園,譚興龍，趙長勝，李曉明

(江蘇師范大學，江蘇 徐州 221116)

由于信號遮蔽、精度制約等問題，GPS難以實現高精度室內定位。而超寬帶UWB技術具有時間分辨率極高、阻礙穿透能力強等特點，在LOS環境下能獲得厘米甚至毫米級的測距和定位精度，適用于室內環境下的高精度定位[1- 4]。

在UWB室內定位中，濾波算法是關鍵環節。在高斯白噪聲情況下，卡爾曼濾波基本可以滿足定位需求。文獻[5]提出將有色噪聲一階AR模型的自適應卡爾曼濾波應用到精密單點定位中。文獻[6]提出為了減小室內環境中障礙物對超寬帶(UWB)傳感器測距結果的影響,使用一種基于卡爾曼濾波(KF)的超寬帶室內定位算法，在復雜環境下可達亞米級動態實時定位精度。文獻[7]提出針對傳統的卡爾曼濾波算法在運用于室內UWB系統定位時,由于初始參數不定以及在環境變化或系統運行偏差后定位誤差增大等問題,提出一種自適應卡爾曼濾波算法。傳統卡爾曼濾波要求觀測噪聲為高斯白噪聲序列，對有色噪聲而言卡爾曼濾波不能直接使用，而粒子濾波可以不受噪聲模型的約束[8]。文獻[9]提出采用多項式長除法將有色觀測噪聲模型展開成無窮級數,截斷取其有限項獲得有色噪聲的先驗信息；然后利用粒子濾波能夠處理非高斯噪聲的特點對有色觀測噪聲進行處理。文獻[10]針對含有色噪聲的語音,提出了一種基于Unscented粒子濾波的單通道語音增強方法。采用時變自回歸模型(TVAR)對干凈語音建模,通過Unscented粒子濾波器估計AR模型的參數并濾除有色噪聲。上述是學者們針對觀測噪聲為有色噪聲情況下，對粒子濾波的研究情況。從粒子濾波出發，文獻[11]提出了基于似然分布自適應調整的粒子濾波算法，該算法選取先驗密度函數作為重要性密度函數。文獻[12]針對粒子濾波算法的實時性較差,計算量隨著粒子數的增加成級數增加,提出一種基于似然分布的樣本數自適應UPF算法，將似然分布與樣本數自適應UPF結合。

本文在前人的工作基礎之上，針對高斯白噪聲和有色噪聲兩種情況，分別將拓展卡爾曼濾波與似然分布自適應粒子濾波應用到UWB定位中，研究這兩種算法的優勢與不同。

1 基于距離的UWB定位原理

考慮一般的行人室內定位問題，假定行人沿直線運動，觀測站坐標為(x0,y0)，狀態方程式為

X(k)=ΦX(k-1)+Gω(k-1)

(1)

式中，Φ為狀態轉移矩陣；G為過程噪聲驅動矩陣；ω(k)為過程噪聲。行人狀態矢量為

X(k)=[x1(k)y1(k)x2(k)y2(k)]T

(2)

式中，x1(k)為東方向位置；y1(k)為北方向位置；x2(k)為東方向速度；y2(k)為北方向速度。

行人觀測方程式為

Z(k)=h(X(k))+v(k-1)

(3)

函數h表示觀測站與行人狀態之間的非線性關系

(4)

式中，v(k)為觀測噪聲。

2 似然分布自適應粒子濾波

采用似然分布自適應調整粒子濾波方法，由精度因子α來自適應調整似然分布狀態，增加先驗和似然的重疊區。改變似然函數的分布即是改變對應粒子權值的分布，因此只對粒子濾波權值更新作改進[13]。似然分布自適應調整粒子濾波(LDAPF)過程如下：

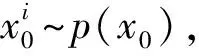
(2) 更新粒子。計算每個粒子的似然概率，同時更新權值。

(5)

(6)

式中，ε為閾值，根據經驗確定；K為比例系數，K/α>0。

(5) 歸一化權值。

3 試驗仿真與結果分析

3.1 跟蹤系統建模

假設行人在室內行走，軌跡為矩形，x方向為東方向，y方向為北方向，初始位置為(0,0)，初始狀態為(0,0,1,0)，其水平速度x2=1 m/s，其余狀態參數均為0，PF中粒子數目為N=200，采樣次數為100。選取拓展卡爾曼濾波、粒子濾波和似然分布自適應粒子濾波，研究它們在高斯白噪聲和有色噪聲下的優勢與不同。

3.1.1 高斯噪聲情況

在高斯噪聲情況下，圖1為行人真實軌跡和預測軌跡，3種算法處理后的誤差及用時對比情況見表1。

圖1表明在高斯白噪聲情況下，EKF算法、PF算法和LDAPF算法均能較好地實現對行人的跟蹤。由表1均方根誤差(RMSE)對比情況可見，位移上EKF算法x方向定位精度為0.113 m，PF算法x方向定位精度為0.134 m，LDAPF算法x方向定位精度為0.078 m。由此可以看出x方向LDAPF算法精度優于PF算法、EKF算法。y方向定位精度各算法差距不大。由速度均方根誤差(RMSE)可看出，3種算法精度均較高，EKF算法較其他兩種算法x方向均方根誤差稍大，但沒有明顯影響運動軌跡。

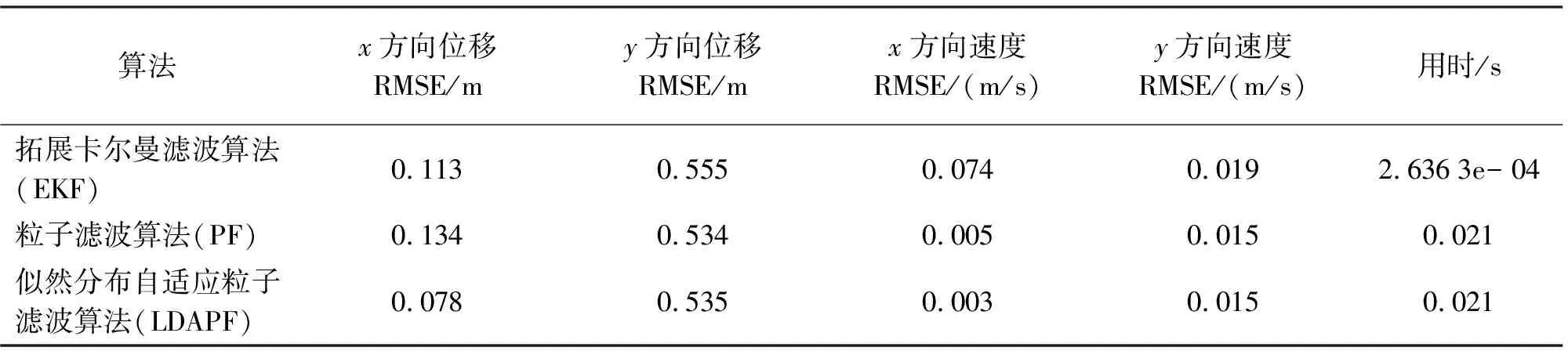
表1 3種算法處理后的誤差及用時對比

在用時上，PF算法和LDAPF算法較EKF算法用時較多，實時性上不如EKF算法。但整體上LDAPF算法在高斯白噪聲情況下的精度優于其他兩種算法，可達到較高的定位精度。

3.1.2 有色噪聲情況

傳統UKF要求噪聲是高斯白噪聲，實際上，由于載體的機制等原因，不同系統的噪聲不一定表現出高斯特性，如GPS動態定位中觀測誤差和動力學模型是具有一定時空相關、異常特性的有色噪聲[14- 15]。

在有色噪聲情況下，圖2給出了預測軌跡，3種算法處理后的誤差及用時對比情況見表2。由圖2可見，EKF算法跟蹤效果較PF和LDAPF兩種算法差。

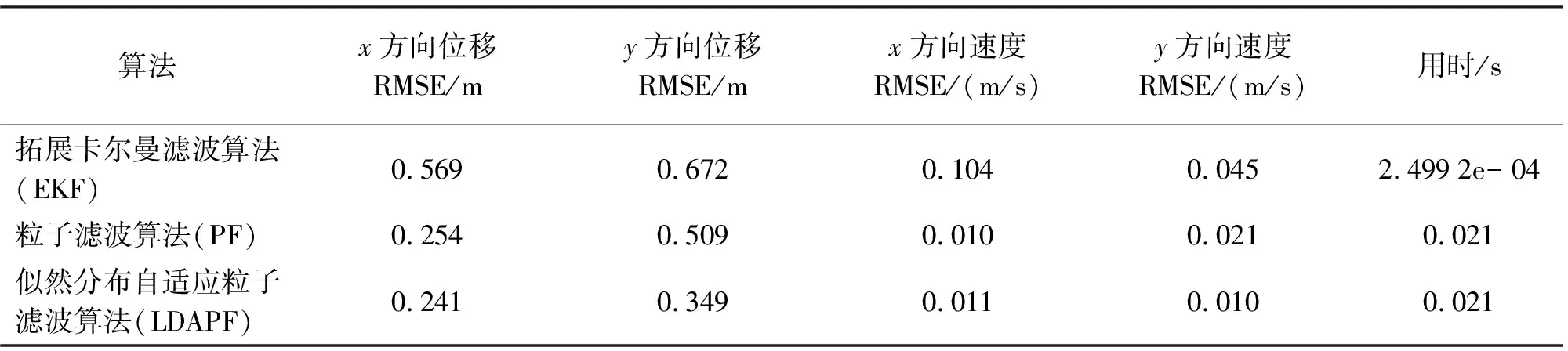
表2 3種算法處理后的誤差及用時對比情況

由表2可見，EKF算法x方向定位精度為0.569 m，y方向定位精度為0.672 m，x方向速度精度為0.104 m/s、y方向速度精度為0.045 m/s，導致x、y方向速度誤差變大，因此在圖2平面跟蹤軌跡圖中波動較大。對于PF和LDAPF算法，在y方向位移上，LDAPF算法較PF算法精度略高出約16 cm，x方向上差別不大。

在有色噪聲情況下，3種算法實時性上與高斯白噪聲情況基本一致。從定位精度上來說，拓展卡爾曼濾波不能直接用于處理有色噪聲的情況，而粒子濾波性能表現良好。在量測精度較高時，LDAPF算法能在一定程度上改善濾波結果，提高定位精度，優于PF算法。

3.2 實例驗證

試驗地點為室內，試驗場景為LOS環境，采樣80次，由測距精度厘米級的通信和測距模塊采集獲得觀測站和UWB流動站的觀測距離。UWB流動站初始坐標為(20.35,17.68),沿預定軌道緩慢移動，采用拓展卡爾曼濾波EKF算法、粒子濾波PF算法和似然分布自適應粒子濾波LDAPF算法分別進行定位解算。

用3種方法進行濾波解算，圖3給出了平面軌跡跟蹤圖。3種算法處理后的誤差及用時對比情況見表3。由圖3可看出，PF算法與真實軌跡比較接近，EKF算法軌跡偏差較大。結合表3，EKF算法x和y方向均方根誤差均大于PF算法的均方根誤差，而PF和LDAPF兩種算法跟蹤效果比較接近。

由表3分析PF和LDAPF算法的不同。x方向位移誤差，LDAPF比PF算法更接近真實值。y方向位移誤差，LDAPF算法均方根誤差小于PF算法。這說明在量測模型精度較高時，似然分布自適應粒子濾波可以進一步提高粒子濾波的精度和可靠性，從而得到精度更高、穩定性更好的UWB跟蹤效果。在速度上PF算法、LDAPF算法均方根誤差相差不大，優于EKF算法。在用時上PF和LDAPF算法時間相同，而EKF算法用時更短。

表3 3種算法處理后的誤差及用時對比情況

4 結 論

對于基于距離的UWB算法而言，重要的環節是選取合適的濾波算法。當觀測噪聲為高斯白噪聲時，可以采取卡爾曼濾波算法計算獲得更好的預測結果。在實際情況中，觀測噪聲如果是有色噪聲，這時直接采用卡爾曼濾波算法受到限制，而粒子濾波算法可以很好地處理觀測噪聲為有色噪聲的情況。同時在量測精度要求較高時，采用似然分布自適應粒子濾波能在一定程度上改善濾波結果，提高定位精度。