基于EMD和RBF神經網絡的大壩形變預測

劉思敏，徐景田，鞠博曉

(1. 中國地質大學(武漢)信息工程學院，湖北 武漢 430074； 2. 武漢大學測繪學院，湖北 武漢 430079)

全球衛星導航系統(global navigation satellite system,GNSS)能夠同時測量多個觀測點位的高精度三維變形，隨著其硬件及軟件的不斷發展和完善，GNSS在結構物變形監測方面表現出獨特的優勢。已有研究表明，利用4 h觀測數據進行基線解算，可實現水平和垂直方向精度分別優于1.5、2 mm[1]的目標。

大壩在運營過程中會發生一定程度的變形沉降。基于實測高精度變形時間序列，對變形機理進行解析，進而建立準確的預測模型對其變形趨勢進行推估，其結果對于大壩的安全監測與預警具有重要價值。目前，已有許多國內外學者在大壩變形預測領域展開了研究。在常用的方法中，BP神經網絡易陷入局部最小值，訓練效果對于網絡結構非常敏感[2- 3]；灰色模型、支持向量機法在歷史觀測數據樣本較大時的預測效果不佳；奇異譜分析法需要相關數據，如水位、溫度等[4- 7]。

GNSS大壩變形數據時間序列具有明顯的多尺度特征，且可視為非平穩時間序列[5]。本文擬采用經驗模態分解[8](empirical mode decomposition,EMD)與徑向基函數(radial basis function，RBF)神經網絡進行大壩變形預測。EMD具有多分辨率及自適應性的特點，能夠較好地處理隨機非平穩信號，與小波變換及其他時域分析方法相比，不受小波基選擇和分解層數的影響，可廣泛應用于時間序列分析、降噪領域、懸索橋動力特性分析[9- 11]。RBF具有最佳逼近及全局最優的優點，同時可快速迭代訓練，因此在非線性時間序列的預測中有廣泛的應用，在混沌時間序列預測、電力系統短期負荷預測、股票價格預測、肝移植存活率預測[12- 15]中均得到了較好的處理結果。綜上，兩者結合可以達到很高的預測精度和良好的泛化能力。

本文利用西龍池上水庫位于主壩上的測點L022的2012年3月—2014年1月共680 d的觀測數據，使用武漢大學自主研發的變形監測軟件DDMS解算獲得測站各方向的坐標時間序列[1]；然后，使用本文所提出的預測模型進行大壩變形預測，并通過與實測變形數據進行對比，分析兩者差值的均方根誤差(RMSE)和平均絕對誤差(MAE)，以評價本文模型的預測效果。經實例分析，該模型預測精度高，泛化性能好，受數據精度影響較小，自動化程度高。

1 預測原理與方法

1.1 EMD基本原理

EMD是基于非線性、非平穩數據的自適應時頻信號分解方法，通過數據的特征時間尺度來獲得本征波動模式，然后分解數據，將原始時間序列分解為一系列由高頻到低頻的本征模態函數分量(intrinsic mode functions，IMFs)和殘余項。

對于信號X(t)，EMD利用所有的局部極值來構建包絡線并確定包絡平均值m(t)，進而求臨時局部震蕩值h(t)=X(t)-m(t)，利用得到的臨時局部震蕩值h(t)代替信號X(t)，重復以上步驟并進行循環，直到m(t)的值近似為零，則h(t)即為第1個IMF分量,記為c(t)，計算殘余項r(t)=x(t)-c(t)，利用r(t)代替信號X(t)重復上述步驟，繼續求下一個的IMF分量和殘余項。

最后，原始信號X(t)經K次分解后可表示為

(1)

式中，rK(t)表示殘余項;ci(t)表示第i個IMF分量。

1.2 RBF神經網絡基本原理

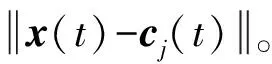
隱含層的輸出為非線性激活函數hj(t)

(2)

式中，bj為一個正標量，表示高斯基函數的寬度；m為隱含層的節點數量。網絡的輸出由如下加權函數實現

(3)

式中，w為輸出層的權值；n為輸出節點個數；y為神經網絡輸出。

1.3 基于EMD和RBF神經網絡的大壩預測模型

本文僅對大壩進行短期的變形預測，具體流程如下：首先從原始數據中通過最小二乘法去除趨勢項，得到新時間序列{X(t)}，對新序列進行自適應經驗模態分解，得到不同尺度的IMF和殘余項，采用RBF神經網絡根據高、低頻IMF采用不同的步長分別預測n個IMF和殘余項，最后疊加各尺度下的預測結果，獲得大壩變形預測值。本文數據處理流程及預測模型結構如圖2所示。

2 工程實例分析

本文以西龍池上水庫GNSS大壩變形監測系統為例，選取水庫主壩體L022號GNSS監測點2012年3月—2014年1月共680 d的變形時間序列進行建模，數據處理采用DDMS軟件，采用4 h時段靜態解算模式，共4080期數據。以1～4000期數據建立RBF神經網絡進行網絡訓練；以4001～4080期數據作為試驗數據。RBF神經網絡的迭代次數為1000，神經網絡結構為24- 1- 1或48- 1- 1，即輸入層的節點數為24或48，隱含層為1，輸出層為1。為降低建模誤差，神經網絡訓練前對4080期數據均進行歸一化處理，預測后反歸一化為真實預測值。

本文首先使用最小二乘法去除原始時間序列中的趨勢項，由于三階擬合能較好地擬合出變形趨勢，因此筆者認為最小二乘三階擬合結果為時間序列的趨勢項。圖3中黑線為原始時間序列，灰線為去趨勢項后的時間序列{X(t)}，去趨勢項后可以更加準確地看出時間序列的周期性波動。

然后進行歸一化處理，并通過EMD分解時間序列， 分解結果如圖4所示。 EMD基于信號本身特點將信號自適應地分解成9個尺度的IMF，時間序列中隱含的不同周期信號被分解成不同尺度的信息。

采用RBF分別預測各IMF和殘余項，得到各IMF和殘余項的預測值，然后疊加各尺度下的預測結果，獲得大壩變形預測值。N、E、U 3個方向的預測結果及誤差如圖5(a)—(c)和表1所示。實測值與預測值在N方向最大誤差為2.6 mm，E方向最大誤差為1.3 mm，U方向受數據本身精度影響，有異常值存在，最大誤差為8 mm，3個方向的RMSE分別為0.878 6 mm(N)、0.360 4 mm(E)和2.235 mm(U)，且預測期數越短，誤差越小。3個方向的高頻部分預測值與實測值吻合度較好，能明顯預測出高頻的走勢。

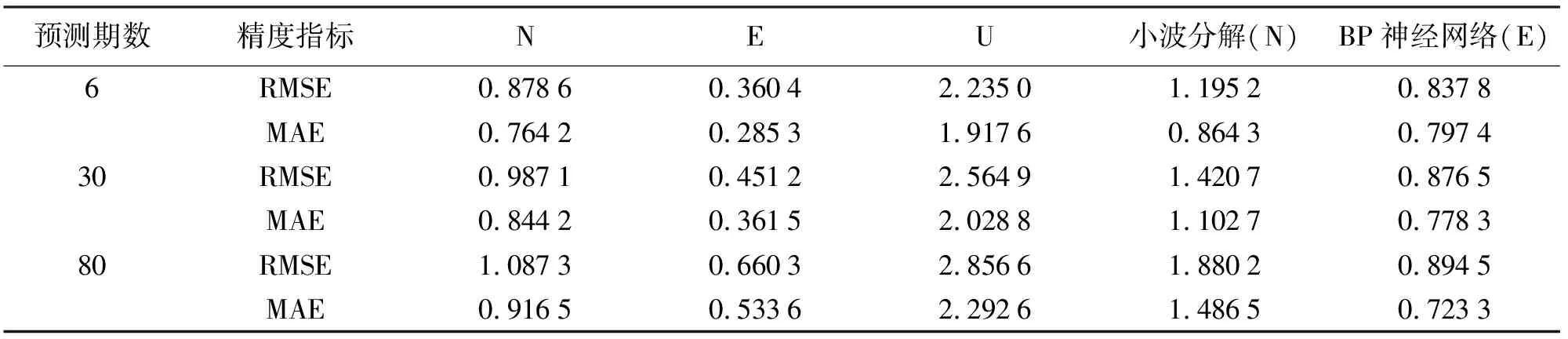
表1 L022號站3個方向的RMSE與MAE mm

為比較EMD方法與小波分解方法在預測準確性上的差異，分別使用兩種方法對N方向的變形時間序列信號進行分解，對分解后的各個分量使用RBF進行預測，并對比其預測精度，結果如圖5(a)、(d)及表1所示。由圖1可知，使用EMD方法對信號進行分解，明顯比小波分解的預測精度更高，高頻部分符合更好。通過表1對比兩者預測結果，本文使用的方法在不同預測期數下的預測精度均明顯高于小波分解。

為了評價本文預測方法的整體預測效果，選用BP神經網絡與本文預測模型的預測結果進行對比。以E方向為例進行對比試驗，兩種預測方法的預測結果如圖5(b)、(e)及表1所示。本文預測方法最大誤差為1.3 mm，高頻部分和低頻部分都與實測值符合較好，能較為準確地反映真實的變形信息；BP方法預測結果的最大誤差為2.7 mm，低頻趨勢預測結果較好，但高頻部分不能準確預測。RBF預測結果的MAE、RMSE較BP分別最高可提高63%、57%。

3 結 語

隨著GNSS自動化變形監測技術在大壩、滑坡、橋梁等領域的廣泛應用，基于大數據、神經網絡等理論和方法的變形預測已成為當前的一大研究熱點。本文針對GNSS大壩變形時間序列的預測問題，提出了一種結合EMD與RBF神經網絡的預測大壩變形的新方法。經對比試驗表明，該方法的預測值與真實值在N、E、U 3個方向的RMSE分別為0.878 6、0.360 4和2.235 mm，具有很高的預測精度和良好的泛化能力。