考慮過程阻尼的銑削穩定性分析
王田,于慎波,范季錚,梁贏東
(沈陽工業大學 機械工程學院,遼寧 沈陽 110870)
0 前言
機械加工中的顫振不僅會降低被加工表面質量和加工精度,而且嚴重時還會損壞刀具與機床[1]。在銑削加工中,顫振是國內外研究的熱點。最早的機床顫振理論是由F.W.Taylor在20世紀初提出的,他認為顫振是由于切削頻率與機床結構中某一部分的固有頻率相同,產生共振所引起的[2]。1946年Arnold首次提出摩擦型顫振理論,他認為摩擦型顫振是由于切削過程中刀具與工件之間在切削速度方向上摩擦作用引起的[3]。T.R.Sisson指出切削過程中切削力與切削速度成反比是產生摩擦型顫振主要原因之一[4]。Peter Stelter將車刀簡化成懸臂梁模型,指出其在受到干摩擦力作用時會發生摩擦型顫振[5]。1954年J.Tlusty首次提出振型耦合型顫振,他指出振動系統在兩個自由度方向上剛度接近時,產生耦合效應從而導致振型耦合型顫振發生[6]。于俊一等通過考慮耦合效應、耦合效應與再生效應的綜合作用,指出機床工藝系統剛度主軸的最佳方位與動態切削力的構成有關[7]。Gasparetto通過建立耦合型顫振模型,分析刀具在切削過程中的運動軌跡,得出了切削的穩定性條件[8]。R.S.Hahn在1954年提出再生型顫振理論,他指出在有振紋的工件表面上進行切削從而引起振紋再生效應,當滿足顫振產生的條件時,就會產生再生型顫振[9]。在此理論基礎上,J.Tlusty和S.A.Tobias在同年指出再生型顫振中的動態切削深度與動態切削力會相互影響,并通過繪制顫振穩定性葉瓣圖分析了切削加工系統在某一切深下的穩定性[10,11]。后來有實驗表明,低速切削加工時,過程阻尼可提高切削穩定性極限,即抑制了顫振。過程阻尼的分析和建模是近年國際學術界的研究熱點[12,13]。Altintas 等將其列為尚未解決的切削顫振中的難點[14]。
Sisson和Kegg等最早注意到低速下工件切削表面和刀具后刀面接觸是阻尼增加的主要原因[15]。李忠群等以考慮過程阻尼的單自由度車削和二自由度銑削穩定性建模分析為基礎,實現顫振穩定性的預測[16]。Tyler等將表面法線方向的過程阻尼力描述為切削深度、切削速度、刀具進給速度和單一經驗系數的函數,獲得了多自由度的動力學系統[17]。Li和Sun等在高階時域算法中把再生效應、螺旋角和過程阻尼引入到銑削系統擴展動力學模型中,保證了計算效率和精度[18]。李鐘昀運用柯西變換改進了二階半離散法,采用該方法和不動點理論預報了銑削穩定性與表面位置誤差[19]。
本文在傳統的銑削動力學基礎上,建立了一種考慮過程阻尼的銑削動力學模型,得到了銑削加工的穩定性葉瓣圖。實驗結果表明,利用考慮過程阻尼的銑削動力學方程得到的穩定性葉瓣圖,比未考慮過程阻尼得到的穩定性葉瓣圖精度更高,在低速區,穩定性區域顯著增加。
1 過程阻尼
在銑削加工中,如果顫振發生,振幅增大。當銑削刀具后刀面和工件加工表面之間存在相互作用時,產生過程阻尼。該阻尼增加了銑削穩定性,特別是在低切削速度下,會對顫振產生抑制作用。圖1描述了過程阻尼機理。
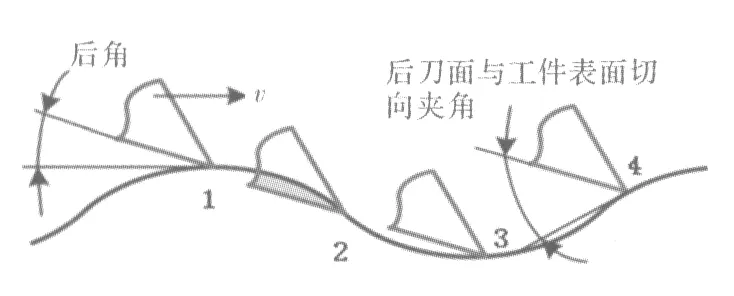
圖1 過程阻尼的描述示意圖
當每個刀齒從被加工工件波紋表面移除切屑時,在1點和3點之間產生過程阻尼力。人們普遍認為,過程阻尼取決于刀具后刀面與工件接觸壓力和刀具后刀面壓入工件的體積。例如2點,后刀面與工件表面切向夾角逐漸減小為負值,壓入體積逐漸增大,干涉作用逐漸增強,這直接導致過程阻尼力的產生。然而,在點4,當刀具在被加工工件波紋表面上向上移動時,干涉消失。Ahmadi和Ismail等[8]指出過程阻尼可以用等效粘性阻尼表示為:
(1)
式中,Ksp為壓痕系數,W為刀具后刀面的磨損帶寬度,a為軸向切削深度,v為切向速度v=πDΩ/60,D表示刀具直徑。
2 考慮過程阻尼的銑削穩定域預測
在二自由度銑削系統中,考慮過程阻尼的銑削動力學模型方程表示為
式(2)中切削力系數表達式為
過程阻尼力表達式為
將式(2)轉換成狀態空間表達式為
(3)
其中,M、C、K、q、H和G分別表示矩陣。
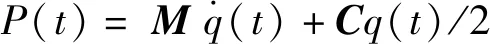
(4)
式中,矩陣A0為系統中時不變的常數項,矩陣A(t)和B(t)由動態切削力決定的周期性矩陣,滿足A(t)=A(t+T)、B(t)=B(t+T),T為時間周期且與時滯量相等。
A(t)=
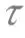
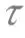
(5)
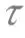
Xk+1=[I-Fk+1]-1[(F0+F0,k)Xk
+Fm-1Xk+1-m+FmXk-m]
(6)
其中
F0=φ0
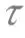
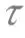
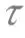
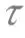
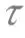
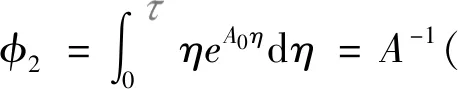
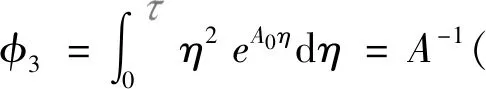
根據式(6)構造離散映射表達式
Yk+1=DkYk
(7)
其中Yk可表示為
Yk=[Xk,Xk-1,…,Xk+1-m,Xk-m]T
(8)
(9)
矩陣P、Pm-1和Pm分別為
P=[I-Fk+1]-1(F0+F0,k
Pm-1=[I-Fk+1]-1Fm-1
Pm=[I-Fk+1]-1Fm
一個完整周期的狀態轉移矩陣可以通過Dk構造出來。即
φ=Dm-1Dm-2…D1D0
(10)
最后,由Floquet理論可知,如果狀態轉移矩陣φ的所有特征值模均小于1,則系統穩定;否則系統處于不穩定狀態。
3 試驗分析與驗證
銑削穩定性驗證試驗在某機床有限公司的G7-龍門式加工中心進行,測試系統如圖2所示。所用銑刀型號為400R16R1006B32和刀片型號為APMT1604PDER-H2。刀具直徑100 mm,刀具齒數為6。進行刀具結構實驗模態分析時,采用B&K3050A型6通道數據采集系統;沖擊力錘型號為B&K8207;加速度傳感器B&K4508B。加工方式為銑槽,工件材料為45#鋼,尺寸為400 mm×400mm×50mm。由槽銑快速標定法獲得切向力系數Kt=827 MPa,徑向力系數Kr=576 MPa,壓痕系數Ksp=1.5×105N/mm3,庫侖摩擦系數μ=0.3[8]。測得刀具的頻響函數如圖3所示。刀具模態參數見表1。

圖2 銑削試驗測試系統
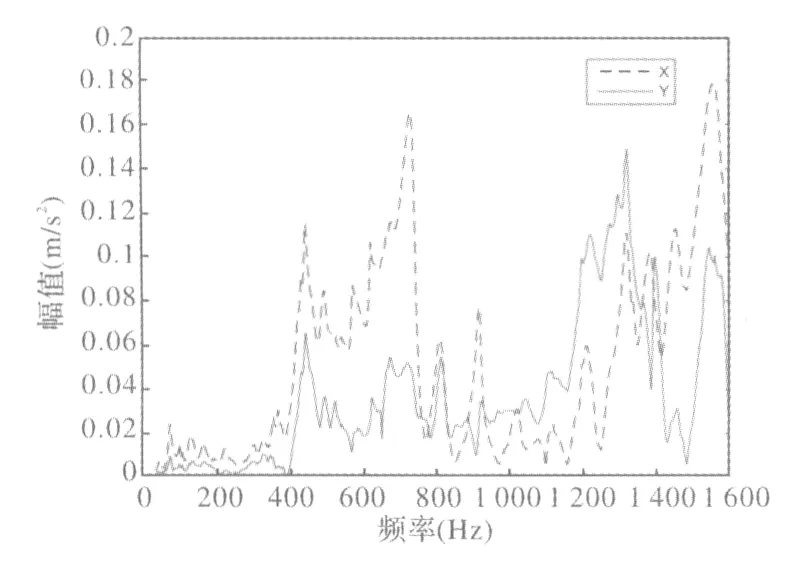
圖 3刀具的頻響函數
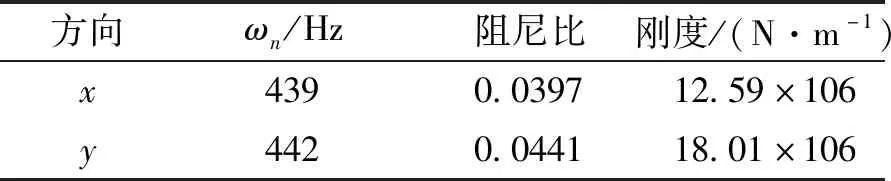
表1 刀具系統模態參數
結合上述參數,利用Matlab編程計算,繪制出未考慮過程阻尼和考慮過程阻尼的穩定性葉瓣圖,如圖4所示。對比分析發現:與未考慮過程阻尼影響相比,考慮過程阻尼影響后低速區的穩定切削區域增加顯著,在高度區穩定性葉瓣圖幾乎是一致的,這意味著在高速切削條件下,過程阻尼對穩定性葉瓣圖的影響不明顯。為了驗證仿真結果的正確性,根據繪制的穩定性葉瓣圖,選取考慮過程阻尼的穩定性葉瓣曲線以下A點(主軸轉速為400 r/min、切削深度為1.5 mm)和以上B點(主軸轉速為400 r/min、切削深度為2 mm)的切削參數進行測試分析,如圖5、圖6所示。通過對所采集加速度信號進行FFT變換,觀察其時域信號及頻域信號的特征,判斷是否發生顫振。
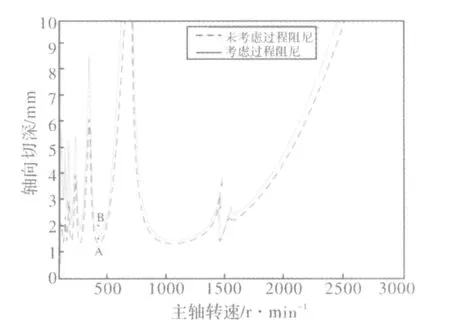
圖4 考慮過程阻尼和不考慮過程阻尼的穩定性葉瓣圖
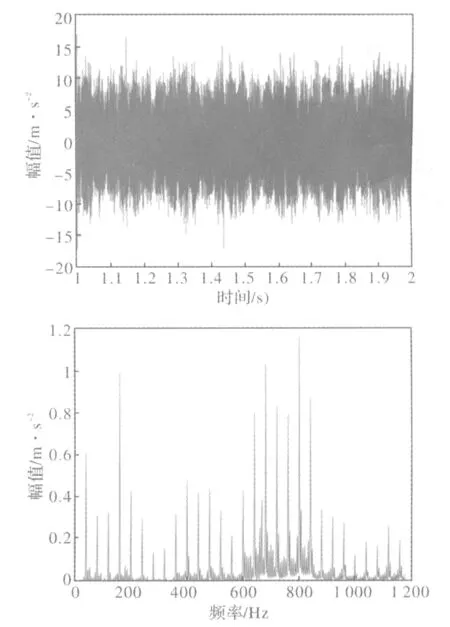
圖5 A點加速度時域及頻域信號(n=400 r/min,a=1.5mm)
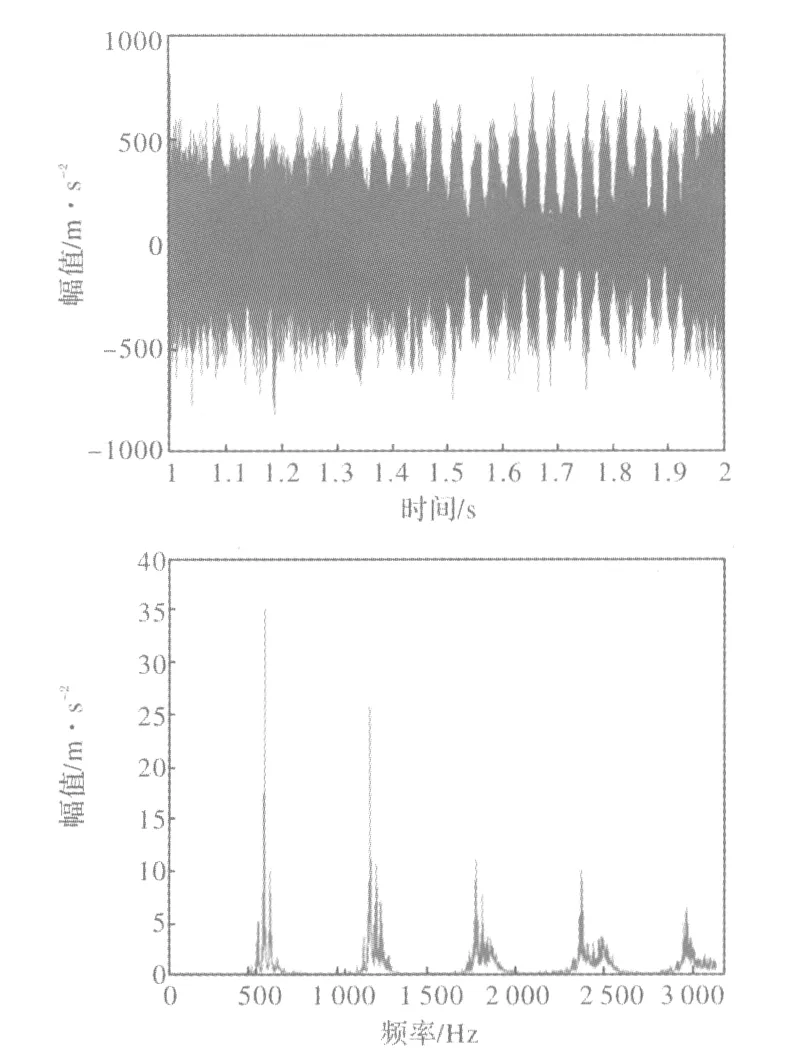
圖6 B點加速度時域及頻域信號(n=400 r/min,a=2mm)
從圖4可以看出A點時域信號平穩可靠幅值較小,頻域信號所顯示的頻率主要發生在齒頻(400×6/60=40 Hz)及其倍頻處。此時,銑削加工過程穩定,沒有出現顫振現象。而在觀察圖5時,可以看出B點的時域信號幅值明顯增大,并在頻域信號中出現了除齒頻及其倍頻以外的新的振動頻率主要峰值頻率為592 Hz、1 184 Hz、1 776 Hz、2 368Hz、2 960 Hz,這些頻率均為592 Hz的倍頻。根據再生型顫振理論,倍周期分叉頻率fPD和準周期分叉頻率fH表示兩種形式的再生型顫振頻率,其計算式分別為
(11)
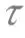
(12)
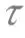
4 結論
(1)在傳統的銑削動力學模型基礎上建立了考慮過程阻尼的銑削動力學方程,得出了穩定性葉瓣圖。通過銑削試驗驗證了模型的正確性。
(2)研究結果表明,在低速區,過程阻尼對銑削穩定性很大影響,穩定性區域顯著增加。用考慮過程阻尼的銑削動力學方程得到的穩定性葉瓣圖,比用傳統的銑削動力學方程得到的穩定性葉瓣圖精度更高。為銑削參數的優化提供了理論支撐和依據。

