曲率約束的激光點云全局優化配準算法

馬偉麗，2，王健，孫文瀟

(1.山東科技大學，山東 青島 266590；2.山東省水利勘測設計院，濟南 250101)

0 引言

在物體表面三維重構[1]中，點云數據配準是最為重要的步驟。使用三維激光掃描技術[2-3]，可以得到被測物體表面點云數據，通過在多個視角下測量的點云數據，然后對多測站數據進行配準，最終獲得完整的三維物體模型。點云數據配準精度，對三維物體模型重構和應用有著直接的影響。

目前，國內外提出了很多數據配準的算法，其中使用最為廣泛的算法就是1992年Besl等[4]提出的迭代最近點算法(ite-rative closest point，ICP)以及它的改進算法[5-6]。為了使數據配準的結果更加準確，ICP算法使用時必須要滿足2個條件：點云之間存在包含關系、點云之間初始位置不可以相差過大。數據配準常用方法有：特征點提取法[7-10]，根據曲率特征、法向量等信息提取特征點，由得到的特征點對完成配準；質心重合法[11]，計算點集的質心，并將2個點集作相對于質心的平移；標志點法[12-13]，人工粘貼標志點，通過標志點配準。上述配準方法，對點云間位姿和噪聲程度有嚴格要求，同時容易陷入局部最優。

針對上述點云數據在配準中存在的問題，本文采用散亂點云建立的曲率信息研究點云的配準方法，在基于曲率特征配準的基礎上，引入現在比較成熟的模擬退火法(simulated annealing，SAA)對點云數據拼接誤差的參數進行尋優，避免局部最優。因此提出基于隨機抽樣一致性算法(random sampling consensus，RANSAC)提取曲率特征點，然后用距離最近原則尋找對應點對，最后使用模擬退火法防止陷入局部最優完成最終配準。

1 經典ICP算法

經典ICP算法[14]利用最小二乘最優匹配原理，通過迭代進行點云之間的剛體變換。首先已知兩塊待配準的重疊點云M和N，其中M為待配準點云，N為參考點云。M點集中的每一點Mi以最小距離原則在N中尋找對應點，對應點構成新的點集。所有對應點對的拼接誤差[15]

(1)

式中：Mi為目標點集；Ni為待配準點集；n為匹配點對總數；λ、R、T分別表示點集M與點集N之間剛體變換的縮放參數、旋轉參數、平移參數。反復迭代求出滿足式(1)且收斂于給定閾值的轉換參數，即為ICP算法配準的最終目的。ICP算法過程描述如下：

①尋找對應點對M’、N’；

②計算配準轉換參數λ、R、T；

③修正待配準點云M得到新的點云M’；

④計算相鄰兩次迭代點集的距離差值di，點對匹配均方差收斂于閾值τ，即di-di+1<τ，則停止迭代，否則令i=i+1，并返回步驟①。

2 改進ICP算法

2.1 曲率特征點集的提取

數據配準時，對于待配準點云M和基準點云N，如果對所有點云進行匹配點的搜索，會非常繁瑣且浪費時間，同時因為噪聲的存在也會對特征點的選取產生影響。本文在進行曲面擬合局部點云時，加入RANSAC算法，以消除噪點的影響，最后利用曲率極值法來提取曲率特征點。

在三維歐幾里得空間中，幾何體結構的特征主要由曲率和法矢量來描述[16]。曲率是一種不隨平移、旋轉、縮放變化的特征，該特征可用高斯曲率KG、平均曲率KM、主曲率k進行描述，首先引入曲率度量公式[17]

(2)

(3)

式中：k1代表最大曲率；k2表示最小曲率；α代表度量曲率相似度。通過公式(2)、公式(3)度量曲率相似度，提取出具有相似結構的點云，然后配準2片點云。特征點提取的具體步驟描述如下：

①選任意一點為種子點，選取K領域計算包含的點個數，計算迭代次數L[18]由式(4)得出：

(4)

(5)

式中：A為點云數；a為擬合曲面方程所需最小點個數，在本文中a=6，P為a個點均為有效點的概率；ε是數據的錯誤率，表示局外點與總數據量之比。

②對點云任意一點，建立鄰域點集合，設曲面方程[19]為

(6)

在K鄰域內隨機選取a個點，計算Qij的初始參數。

④重復步驟②～③，直到循環次數達L次，找到最大局內點，由參數曲面方程解出最優參數Qij。

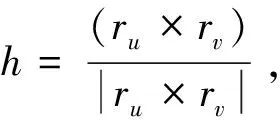
(7)

(8)

⑥由求得的高斯曲率與平均曲率可直接求解主曲率

(9)

(10)

⑦判斷該點主曲率k1或k2在對應的主方向上是否為極值，若為極值，則保留該點，進行下一個種子點判斷。重復步驟⑦～⑧，直到遍歷完所有的數據。

⑧曲率極值越大特征越明顯。為曲率極值設定一個閾值ω，大于該設置閾值則保留曲率特征點，反之刪除。選取曲率特征點集流程圖如圖1所示。

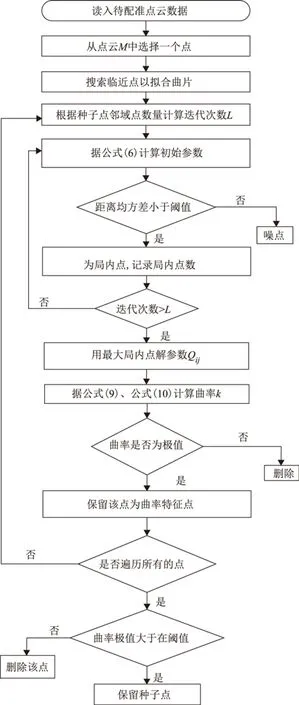
圖1 選取曲率特征點集流程圖

2.2 獲取全局最優轉換參數

配準的過程即是求解待配準點云到基準點云的縮放參數λ、剛性旋轉R和平移T的過程。待配準點云M中的A點和基準點云N中的B點，表示的是地球表面物體的同一個點，可以通過縮放、旋轉和平移變換把A點和B點重合在一起。A點坐標XA，YA，ZA，B點坐標XB，YB，ZB，轉換的公式為：

(11)

在實際測量中，點云的采集不可避免帶入噪聲，雖然根據曲率特征選取特征點，以距離最近為判斷依據獲得相對應的特征點對，但是點云間數據沒有絕對的一一對應關系，因此引入模擬退火法，得到使目標函數最小的最優轉換參數λ、R、T，避免配準時出現局部最優解。目標函數的形式多樣化，本文使用拼接誤差公式(1)作為目標函數。

在1953年，Metropolis[20]等率先提出了模擬退火法。模擬退火法是一種非線性反演，能夠避免使反演陷入局部極大值，是一個不斷尋優的過程。在此過程中，擬合度隨迭代次數的增加呈現一種跳躍起伏的現象，但總體的趨勢是變小或變大，然而正是由于模擬退火允許擬合誤差變大或擬合度變小，進而使得模型從局部的最優值中跳出來，最終得到全局的最優化模型。因此引入模擬退火法，在點云拼接過程中以拼接誤差Eλ，R，T為目標函數，進行優化求解。

在模擬退火法的迭代過程中，要求溫度隨著迭代次數的增加而緩慢降低，由冷卻進度表控制溫度t的逐步下降，同時依概率接受惡化解。接受概率參數是關于溫度t的函數，隨著t不斷的降低，接受概率也不斷降低，直到最后不再接受任何惡化解。本文采用雙曲下降型[21]退火方案。模擬退火法尋找轉換參數的最優具體解步驟：

①初始化目標函數模型參數λ0、R0、T0，確定參數變化范圍，選擇初始溫度t0=1°。

②計算目標函數值E0λ0，R0，T0。

③對當前模型參數進行擾動，產生新的模型參數λ1、R1、T1。

④計算新模型參數下的目標函數值E1(λ1，R1，T1)。

⑤計算目標函數差ΔE，ΔE=E1-E0。

⑥判斷新模型參數是否接受，依Metropolis準則[22]為判斷依據：若ΔE<0則接受；若ΔE>0，則新模型參數以概率P進行接受。

P=exp-ΔE′/t

(12)

式中：t為溫度。

⑦接受新的模型參數時，設置λ0=λ1，R0=R1，T0=T1。

⑧在溫度t下重復一定次數的擾動接受。

⑨降溫t

tG=t0αG1/a

(13)

式中：t0為初始溫度；G為迭代次數；α為給定常數，本文α=1。

⑩重復步驟③至⑨，直到收斂條件滿足。

2.3 改進ICP算法流程

改進配準點云的ICP算法步驟如下：

①讀取需要配準的2個點云：待配準點云M，基準點云N。

②利用RANSAC算法的二次曲面法對其K鄰域進行曲面擬合。

③根據結合式(9)、公式(10)計算該點主曲率k1、k2，并判斷是否為曲率極值點，遍歷所有點云數據，并刪除小于閾值μ的曲率特征點，得到基準點集M’。

④根據②、③計算待配準點云數據的曲率特征點，得到待配準點集N’。

⑤令為M’0、N’0迭代運算初始點集

⑥以距離最近為依據，查詢特征點對(M’0、N’0)。

⑦根據步驟⑥獲得的對應點集使用四元數法計算，獲取縮放參數λ、旋轉參數R、平移參數T。

⑧使用步驟⑥獲得的λ、R、T對點云M利用公式(11)進行變換，得到新的點云。

⑨依模擬退火法判斷是否為全局最優，既公式(1)全局最小，是則保留，否則重復⑤至⑧直到拼接誤差為全局最優，最終完成配準，算法流程圖如圖2所示。

圖2 算法流程圖

3 實驗驗證與結果分析

為了驗證本文算法的正確性、有效性和實用性，進行以下2組實驗。實驗數據采用斯坦福大學的Horse點云模型和Trimble TX8掃描儀采集某教學樓點云數據進行數據配準實驗。所選用的2組數據都有十多種點云視角數據，在每組數據中隨機選取2種視角進行配準，并與經典ICP算法進行比較。本文算法是在經典ICP算法基礎上進行的改進，算法中加入了噪聲點的剔除和避免出現局部最優，使其相對于經典ICP算法針對部分重疊點云的配準問題得到較好的結果。實驗在Matlab 2010b軟件環境下編程實現。

3.1 實驗一

圖3 Horse點云配準結果

為驗證本文方法的正確性，本文對所選用斯坦福大學的Horse點云數據進行配準，并將本文方法與經典ICP算法配準結果進行比較。圖3為Horse點云配準結果圖，紅色點云為基準數據，綠色點云為待配準數據，其中圖3(b)為經典ICP算法配準結果，圖3(c)為本文所提改進算法配準結果。

從圖3可以直觀地看出采用經典ICP算法配準結果較差，兩站點云不能很好地貼合在一起，雖然兩站點云有一部分可以配準在一起，但是仍有大量點云數據配準失敗；而本文所提算法配準結果較好，經計算對應特征點對距離中誤差為2.7×10-3mm。雖然本文所提算法會增加配準時間，但配準結果可以體現出本文所改進的算法可以很好地克服經典ICP算法容易陷入局部最優解的情況。

3.2 實驗二

為驗證本文算法的通用性和實用性，選取Trimble TX8掃描儀采集某教學樓的點云數據為實例進行驗證。所選用的某教學樓點云數據有十多站點云視角，在實驗數據中隨機選取兩站數據進行配準，并與經典ICP算法進行比較。圖4為兩站點云配準前后對比圖，紅色點云為待配準點云M，綠色點云為基準點云N。未配準的兩站數據如圖4(a)所示，用本文算法配準后點云數據如圖4(b)所示。

圖4 整體點云配準前后對比圖

本文為驗證該方法的穩定性和避免局部最優，采用2種算法對某教學樓的2個不同視角的點云進行配準。圖5為2種算法局部配準結果圖，其中圖5(a)為ICP經典算法的精確配準圖，圖5(b)為為本文算法的精確配準圖。

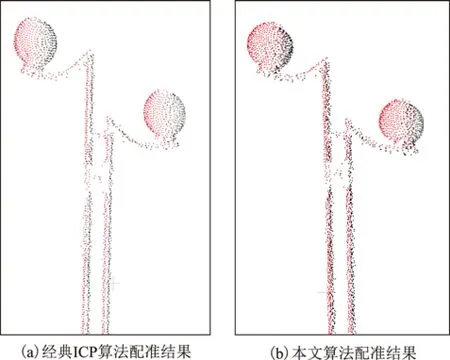
圖5 2種方法局部配準結果

從圖5可以直觀地看出利用經典ICP算法配準后，待配準數據和基準點云數據之間有傾斜、錯層現象。本文所提算法使兩站點云數據相互重合優于經典ICP算法。因此，利用本文算法可以更為精準地進行配準，同時穩健性更強。

為定量描述本文方法的配準效果，在配準后的點云數據中選取房屋角點作為特征點，計算配準后對應角點的距離，繪制距離誤差圖，如圖6所示。在獲取到的點云數據中，很難找到2個對應的點數據表示真實物體的角點，本文利用平面擬合獲取待評價角點周圍的3個平面信息，進而通過3個面相交得到角點坐標。

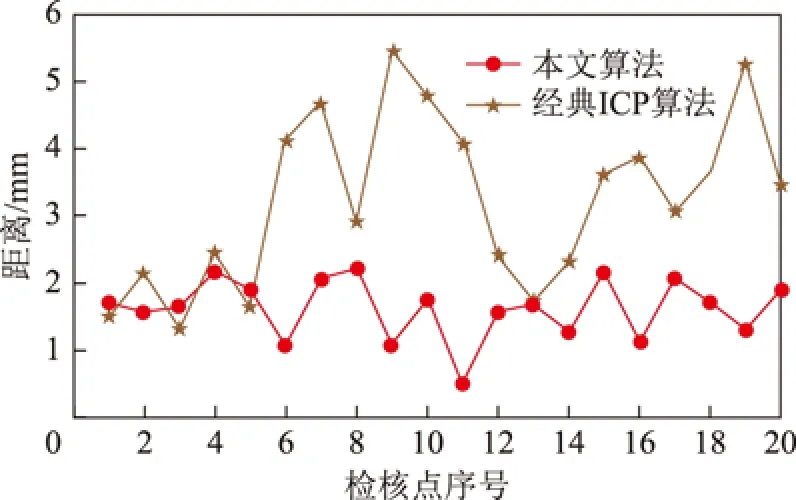
圖6 配準后對應角點距離殘差

從圖6可以清晰看出利用經典ICP算法配準后，大部分檢核點的配準誤差在2 mm左右，但有部分檢核點配準誤差大于5 mm，這是由于通過經典ICP算法進行配準，出現局部最優情況而產生影響。本文算法在提取的特征點時加入結合RANSAC算法，從而去除噪聲的影響提取特征點，同時利用模擬退火算法得到最優的轉換參數，使配準誤差優于2.5 mm，且誤差分布較均勻。實驗配準圖和實驗獲得的對比數據，充分表明本文所提配準方法比經典ICP算法更穩定、精度更高。

4 結束語

在多視角測得散亂點云數據的情況下，利用經典的ICP算法得到的配準結果穩定性不高，容易陷入局部最優。針對這一問題，本文在經典ICP算法的基礎上，引入了一種模擬退火算法尋找全局最優的配準方法。該方法的核心思想是結合RANSAC算法剔除粗差點從而達到穩健的效果，采用模擬退火算法避免點云配準陷入局部最優使得拼接誤差最小，得到全局最優完成數據精確的配準。實驗結果表明，本文數據配準算法提高了配準的穩定性和配準精度，能夠滿足多視角點云數據的配準要求，驗證了本文提出算法的可行性。