一類半線性橢圓型方程邊值問題的可解性研究

田夢甜，鐘金標

（安慶師范大學數學與計算科學學院，安徽安慶246133）

文獻[1]考察了下列半線性橢圓型方程邊值問題

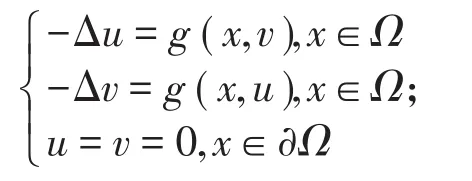
設（1）式中的非線性函數F(x,u)滿足下列條件（或部分條件）：關于在上非負局部Holder連續，即，其中M為一個正常數關于s在單調遞減；關于s在上單調遞減。

1 解的存在性研究

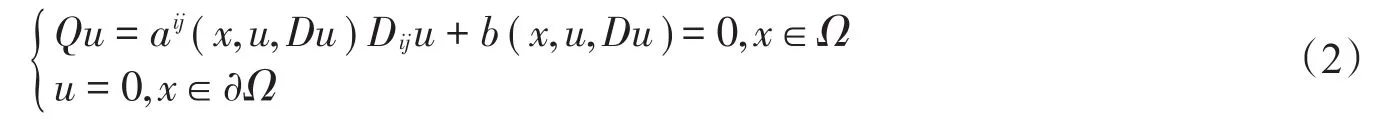
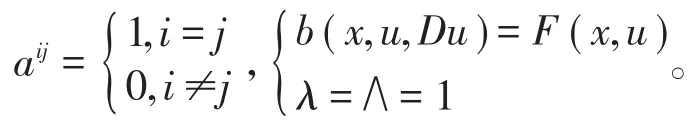
引理1[1]設在Ω中，假設Ω有界，則。

引理2[1]設Q在有界區域Ω中是橢圓的，并假定存在非負常數μ1和μ2，使得：則如果在Ω中滿足，就有，其中又如果在Ω中，則有

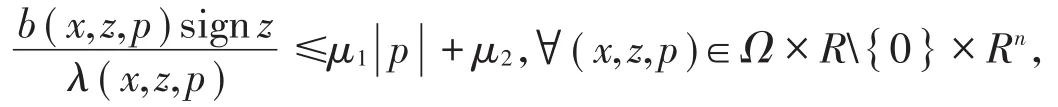
引理3[1]設T是Banach空間B到自身中的緊映射，又設存在一個常數M，使得，對所有滿足的x成立，則T有一個不動點。

定義算子T如下，設u=Tv是半線性橢圓型方程Dirichlet問題：

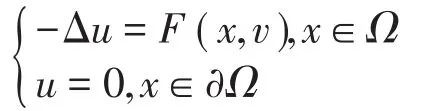
定理1 若條件(A2)成立，則問題（1）的解只能是正解。

證明 由條件(A2)及問題（1）方程可得：

例1 考察問題

解的存在性，其中Ω為Rn中有界光滑區域。因滿足條件由定理2知，問題（4）存在有界正解。

2 解的唯一性定理

定理3 若條件(A4)成立，則問題（1）至多只有一個正解。

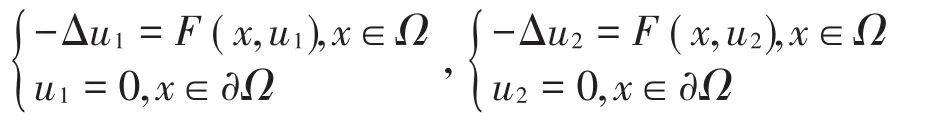
證明 設u1、u2為問題（1）的任意兩個正解，則有成立，兩個方程相減得：兩邊乘以u1-u2后在Ω上積分，并利用Green第一公式得，由 條 件知 ，從而得即結合知即問題（1）至多只有一個正解。

定理4 若條件(A5)成立，則問題（1）至多存在一個有界正解。

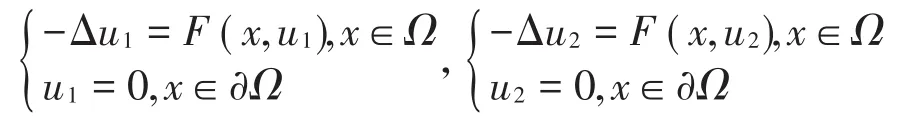
證明 設u1,u2為問題（1）的任意兩個正解，則有成立，從而，因此，，兩邊乘上，并在Ω上積分，同時由可得：再由條件可得：u1≡u2，從而問題（1）至多只有一個解。

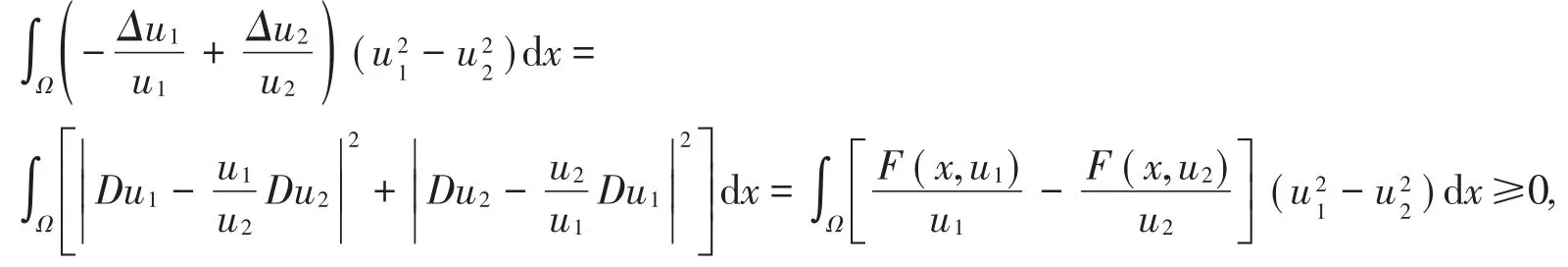
3 總結

本文通過考察半線性橢圓型方程邊值問題的解，研究解的存在性并且給出解的唯一性定理，同時給出了證明。文中（A1）到（A5）是函數F(x,u)所分別滿足的5個條件，這5個條件在不同定理中使用會得出不同的結論，從而得出文章的4個重要定理。