構造給定極點的有理插值新方法

張玉武

（六安職業技術學院基礎部，安徽六安237158）

插值法是一種古老的數學方法，基本做法是通過給定已知點的信息，構造一函數，估算其他點處的函數值，常用的插值方法有多項式插值、有理函數插值等。常用的多項式插值方法有Lagrange插值、New ton插值、Herm ite插值等，它具有結構簡單便于構造、插值函數存在且唯一的特點[1]。對于插值節點較少時效果較好，當等距插值節點增多時，會出現激烈的震蕩，產生Runge現象。有理函數插值常用的有Thiele型連分式插值、重心有理插值等，它比多項式插值要復雜得多，主要表現在有理函數插值未必一定有解、難以避免極點的存在和控制極點位置等。本文基于多項式插值，給出構造給定極點的有理插值新方法，數值例子表明新方法具有較好的逼近效果。

1 有理函數插值

滿足

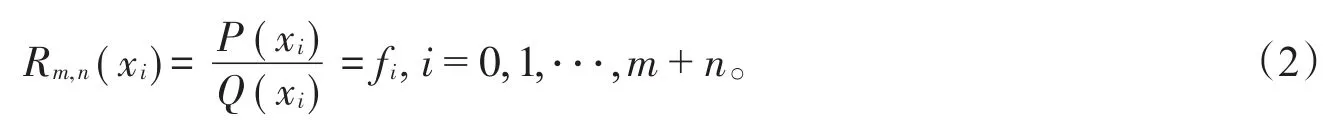
構造有理插值函數需要通過（1）、（2）式求解線性方程組，計算量較大。基于逆差商的Thiele型連分式插值是構造有理插值函數常用方法[2]，通過構造如下形式的連分式函數為f(x)在節點處的l階逆差商，其中，使得成立。

Thiele型連分式插值，不需要求解線性方程組也可以實現有理插值函數的求解，而且具有表達式簡單、計算方便的優點，然而，它無法避免極點的出現，也無法控制極點的位置。對于給定極點的有理插值，朱功勤等[3]、張瀾等[4]基于Thiele型連分式插值分別給出了給定極點的有理函數插值的構造方法。Schneider等給出了重心有理插值方法[5]，其公式為

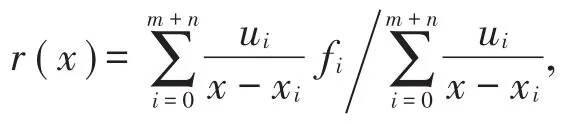
基于多項式插值構造給定極點的有理插值，可以繼承多項式插值結構簡單、插值函數唯一的特點，與上述構造給定極點有理插值方法相比較，還具有便于構造、逼近效果好的優點。

2 構造給定極點的有理插值

按照上述構造給定極點的有理插值方法，只要r(x)分子、分母在節點處的值都不等于零時，構造的有理插值函數不但滿足插值條件，而且完全保留了給定極點信息的優點。

3 數值例子

例1 給定插值節點如表1所示，同時x=-3為一重極點，x=4為二重極點，構造有理插值

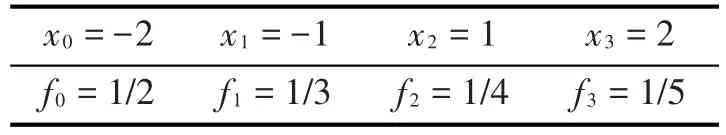
表1 插值條件

表2 新插值條件

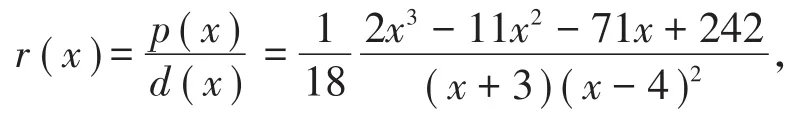
有理插值函數r(x)不但滿足插值條件，而且保留了極點的信息，每個給定極點都保持了原有的重數，同時沒有出現新的極點。

例2 設f(x)=cos(-x)/(x-1)2，插值節點如表3所示。

表3 插值條件

解 按照文中的新方法，可以構造有理插值函數：分別繪制f(x)、r1(x)圖像如圖1所示，誤差圖像如圖2所示。由圖1和圖2看出，新方法構造的有理插值在插值區間內具有很好的逼近效果，誤差很小。

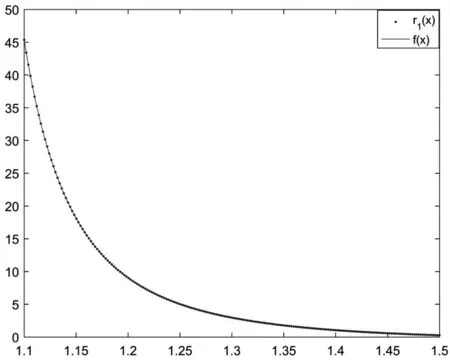
圖1 f(x)與r1(x)圖像

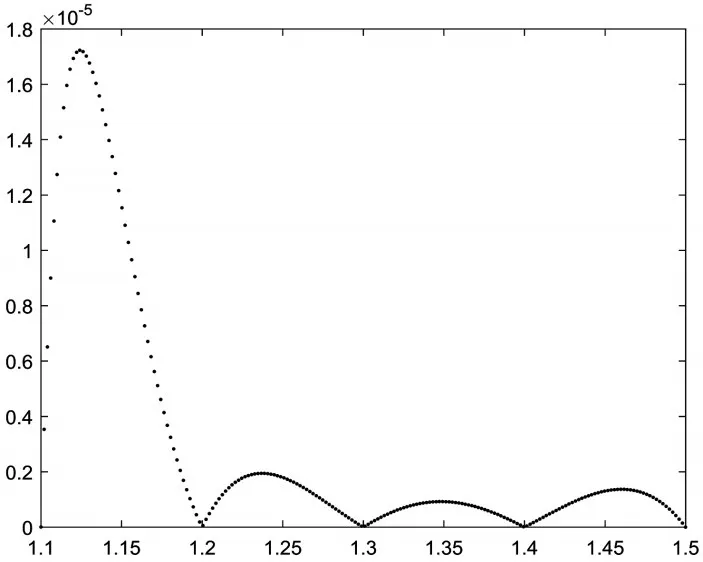
圖2 |r1(x)-f(x)|圖像

為了說明新方法的有效性，將文獻[3]、文獻[4]給出的方法構造插值函數，分別記為r2(x)、r3(x)，計算部分點處的誤差如表4所示。通過比較可以看出，用本文方法構造的有理插值函數的誤差比其他兩種方法給出的插值函數的誤差明顯要小。

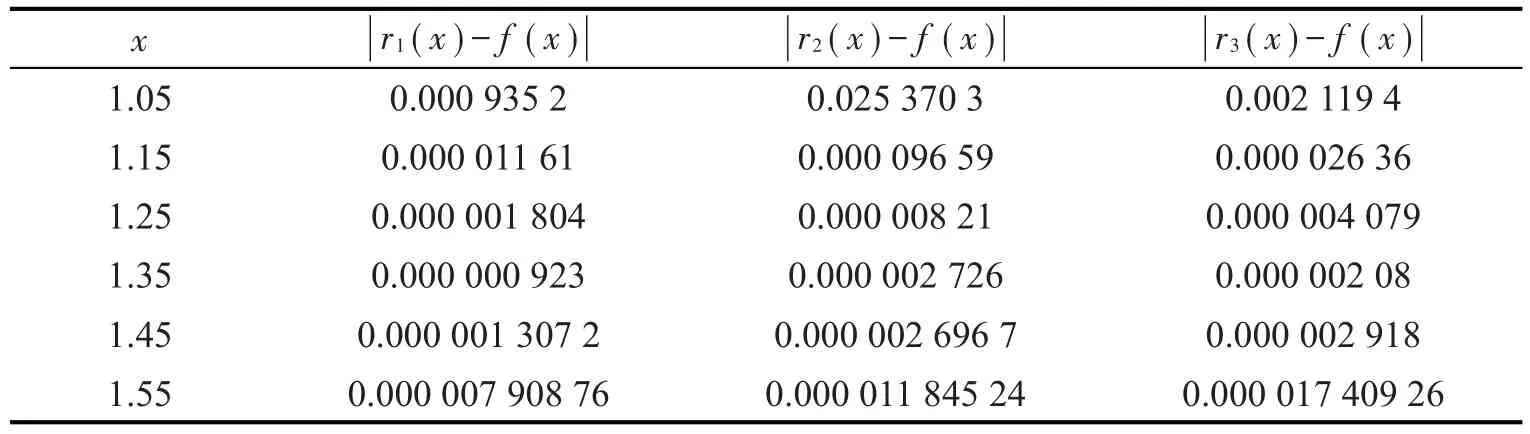
表4 誤差

4 結論