基于主成分分析模型的高職數學課信息化教學評價

摘? 要：信息化在高職數學課中不斷的發展迫切需要建立符合高職數學課特點的評價體系，針對于此，本文提出了注重基礎、突出應用、強化跟蹤為核心的信息化教學評價體系，該評價體系分為9個評價指標，據此指標，以某高職院校的5名數學教師為例，建立了主成分分析模型，此模型均具有客觀性強，易操作的特點，這對高職數學信息化教學定性和定量評價有較強的借鑒作用，也對進一步提高高職數學信息化教學水平有著十分重要的意義。

關鍵詞：數學信息化教學;教學評價;主成分分析法

中圖分類號：G434;TP399? ? ? 文獻標識碼：A 文章編號：2096-4706（2019）23-0101-03

Higher Vocational Mathematics Course Information Teaching Evaluation

Based on the Principal Component Analysis Model

FENG Qiang

（Weifang Vocational College，Weifang? 262737，China）

Abstract：The continuous development of informatization in higher vocational mathematics course urgently needs to establish an evaluation system which is in line with the characteristics of higher vocational mathematics course. In view of this，this paper puts forward an evaluation system of informationization teaching，which focuses on the basis，highlights the application and strengthens the tracking. The evaluation system is divided into nine evaluation indicators. Based on these indicators，five mathematics teachers in a higher vocational college are taken as an example to establish the principal component model. This model is objective and easy to operate. It can be used for reference in qualitative and quantitative evaluation of mathematics informatization teaching in higher vocational colleges. It is also of great significance to further improve the level of mathematics informatization teaching in higher vocational colleges.

Keywords：mathematics informationized teaching;teaching evaluation;principal component analysis

0? 引? 言

隨著信息化與網絡技術的發展，高職院校高等數學課也逐漸從傳統教學模式向信息化教學模式過度，尤其是近幾年，隨著智能手機的普及化以及大量網絡課程資源及對應APP的出現，很多高職院校高數教師針對此現狀從教學組織、教學內容、教學方法、教學反饋等各方面做了對應的改革，與之對應的高職數學課的信息化教學評價也要適應此形式，從而更好的引導以促進高職數學課的教學。

1? 高職數學課教學評價指標構建

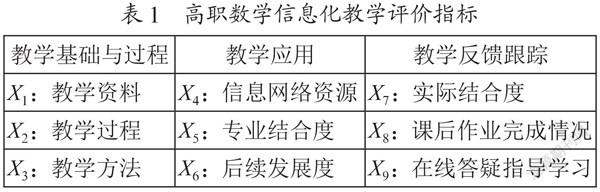
區別于傳統的教學評價，信息化教學化評價更注重多維度綜合評價高職數學課，通過對信息化教學背景下高職數學課的分析，并根據人才培養方案和課程標準，建立了以注重基礎、突出應用、強化跟蹤為核心的信息化教學評價體系，此評價體系在評價指標中更加側重了多媒體資源及網絡資源的有效使用，依此，設定9個評價指標，如表1所示。

針對此9個目標采用主成分分析法進行評價。

2? 資料的來源

該文章資料來自于對5名某職業院校高數教師任課班級情況調查，這5名教師分別用字母A、B、C、D、E表示，X1至X9各指標的分值來源于校內外專家及同行評價。X1至X9均為高優指標，故不必進行同趨勢化處理。

3? 基于主成分分析模型的信息化教學評價

主成分分析法是將原來變量重新組合成一組新的相互無關的幾個綜合變量，同時根據實際需要從中可以取出幾個較少的總和變量并盡可能多地反映原來變量的信息的統計方法。這是數學上處理降維的一種方法，主成分分析法可以消除變量間的相關影響，所以在指標選擇上相對容易些。

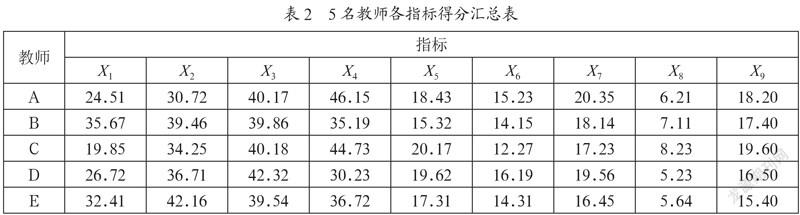
首先將校內外專家及同行教師對A、B、C、D、E這5名教師的X1至X9各指標評價得分匯總，如表2所示。

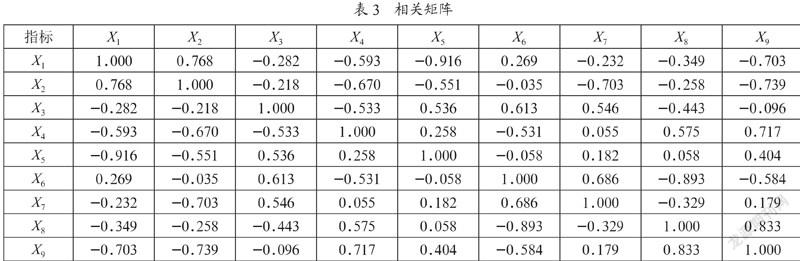
利用SPSS軟件處理數據，得X1—X9相關系數矩陣如表3所示。

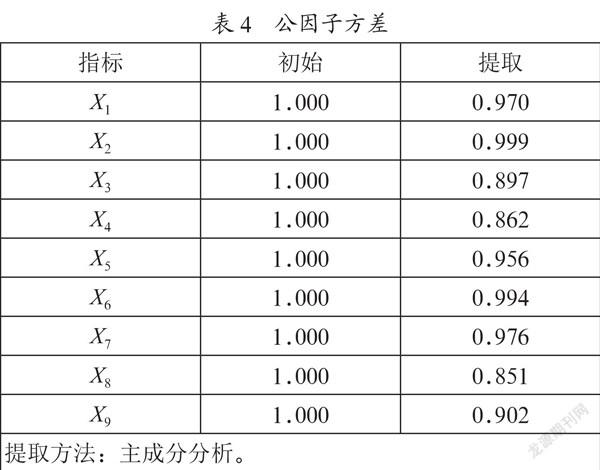
從表3中可以看出教學資料X1與教學過程X2;后續發展度X6與教學方法X3及實際結合度X7;在線答疑指導學習X9與課后作業完成情況X8及信息網絡資源X4存在著顯著關系，這說明這幾個指標信息存在著重疊，這是符合實際的，表4為公因子方差矩陣。

從表4可以看出各個指標的提取率是非常高的，這說明信息得以充分的提取。

對表1至表4中數據進行分析得到表5，并提取前三個主成分。

表5中可以看出前三個主成分的累計貢獻率達到了93.420%，這說明降維后信息保持率維持較高水平。表6為初始因子載荷矩陣。

由表6可以看出信息網絡資源X4、專業結合度X5、課后作業完成情況X8、在線答疑指導學習X9這四個指標在主成分上F1有較高載荷，說明主成分F1基本反映了這些指標的信息;教學方法X3、后續發展度X6、課后作業完成情況X8在主成分F2上的載荷較高，說明主成分F2基本反映了這三個指標的信息;信息網絡資源X4、實際結合度X7在主成分F3上的載荷較高，說明主成分F3基本反映了這兩個指標的信息。

用成分矩陣中的數據除以主成分相對應的特征值開平方根便得到三個主成分中每個指標所對應的系數，即為對應的特征向量，將得到的特征向量與標準化后的數據對應相乘得到主成分表達式：

F1=-0.41X1-0.37X2-0.07X3+0.41X4+0.28X5-0.30X6+0.05X7+0.37X8+0.46X9

F2=-0.23X1-0.31X2-0.49X3-0.10X4+0.32X5+ 0.43X6+0.47X7-0.31X8-0.01X9

F3=0.29X1-0.32X2-0.35X3+0.32X4-0.53X5+0.24X6+ 0.49X7-0.20X8+0.09X9

從而得到權重綜合模型：

（λ1=4.176，λ2=3.082，λ3=1.150）

即：F=0.497F1+0.367F2+0.138F3

根據得出的主成分綜合模型可計算綜合主成分值，并對這5名教師進行排序，進行綜合評價比較，結果如表7所示。

對得出的綜合主成分（評價）值，可用已有的經驗與原始數據做聚類分析進行檢驗，對有爭議的結果，可采用其他的評價方案解決爭議。

4? 結? 論

在主成分分析中，所提取的前3個主成分的累計貢獻率達到了93.420%，首先這說明變量降維后的信息量保持在一個較高水平上，其次這些被提取的主成分能否符合當前高職數學信息化教學的規律及實際，與專家評議打分有著一定的關系;另外主成分解釋其含義一般多少會帶點模糊性，不像原始變量的含義那么清楚、確切，這是變量降維過程中不得不付出的代價;再次主成分分析法評價效果的好壞也與指標之間相關程度有關，一般情況下指標之間相關程度越高，主成分分析效果越好，而主成分分析法具有可消除各個變量之間相關影響、減少指標選擇工作量、評價權重客觀、計算比較規范、便于在計算機上實現的優點。

參考文獻：

[1] 王青華，向蓉美，楊作廩.幾種常規綜合評價方法的比較 [J].統計與信息論壇，2003（2）：30-33.

[2] 楊德芹.教學質量評價模型及案例分析應用研究 [D].武漢：華中師范大學，2008.

[3] 周源.職業院校信息化課堂教學有效性研究 [J].信息與電腦（理論版），2015（21）：170-171+173.

[4] 邱東.多指標綜合評價方法 [J].統計研究，1990（6）：43-51.

作者簡介：馮強（1979-），男，漢族，山東青州人，講師，碩士，研究方向：應用數學教學與研究。