動態(tài)下電磁閥控對靶噴霧流量特性及控制方法
代祥 肖靜 徐幼林 宋海潮

摘要:本研究對電磁閥控對靶噴霧系統(tǒng)動態(tài)條件(噴頭開啟數(shù)、開啟時間、流量大小適時變化)下各參數(shù)[系統(tǒng)壓力(P)、電磁閥頻率(f)、占空比(D)]控制下的噴霧流量(Q)特性進行試驗研究,并利用BP神經(jīng)網(wǎng)絡及遺傳算法(GA)優(yōu)化的BP神經(jīng)網(wǎng)絡對試驗數(shù)據(jù)進行擬合和測試。試驗結果表明:P每增大0.05MPa,Q的最大調節(jié)范圍增加約200 ml/ min;較大的P會輕微減小流量控制線性區(qū)間(I),而較高的f則顯著減小線性區(qū)間(I),f=20Hz,P為0.l0~0.35 MPa時對應的I約為0.3~0.6;Q與各控制參數(shù)間均存在非線性關系,利用BP神經(jīng)網(wǎng)絡進行噴頭精準流量控制誤差較小,平均誤差僅0.20,經(jīng)GA優(yōu)化的BP神經(jīng)網(wǎng)絡具有更高的精度,誤差低至0.15。綜合考慮系統(tǒng)動態(tài)條件下電磁閥各參數(shù)可以實現(xiàn)流量的精準調節(jié),依靠BP神經(jīng)網(wǎng)絡,尤其是GA優(yōu)化的BP神經(jīng)網(wǎng)絡,可實現(xiàn)電磁閥控對靶噴霧流量的精準控制。
關鍵詞:電磁閥控對靶噴霧;動態(tài)條件;流量特性;BP神經(jīng)網(wǎng)絡;遺傳算法
中圖分類號:TP391.41;S220.3
文獻標識碼:A
文章編號:1000-4440(2019)02-0476-08
精準對靶噴霧具有減少農藥浪費,提高農藥利用率的優(yōu)點[1-2]。國內外均對精準的對靶施藥方式進行了大量的研究[3-5],其中施藥量的精準控制是對靶噴霧的核心要求之一[6,8]。施藥量的調節(jié)主要依賴3種方式:壓力調流式、在線注入式以及電磁閥控制式。壓力調流式具有噴霧流量受壓力變化影響明顯的弊端,且實際的噴霧效果受壓力影響較大[9]。在線注入式雖可避免預混及農藥剩余,但是存在藥水難以精準配比,響應延時及混合不均勻的問題,尚未得到實際應用精準對靶噴霧技術中,采用電磁閥控制的噴霧流量調節(jié)方式有著系統(tǒng)相對簡潔的優(yōu)點,是對靶噴霧技術實用化的熱點方向[3-14]。吳春篤等[15]對電磁閥控制的變量噴霧系統(tǒng)中的霧滴沉積模型進行了研究,了解了其典型特征。進一步地,鄧巍等[16]對該系統(tǒng)的霧化特性、霧滴速度進行了研究;翟長遠等[17]對系統(tǒng)中安裝的4種噴頭的流量特性進行了研究,獲得了各噴頭流量與壓力以及占空比之間的擬合關系;魏新華等[18]設計了噴施控制器,并對其進行了測試,結果表明采用比例溢流閥的控制策略可減輕噴頭流量控制不精確的問題,但精準度尚待改進;蔣煥煜等[19]采用卡爾曼濾波的方法經(jīng)分段線性擬合獲得了噴頭流量模型;李龍龍等[20]研究了應用高頻電磁閥條件下的噴霧特性,指出噴頭流量的控制非單因素影響,而是多種影響因素共同作用的結果。總體上,雖然電磁閥控制的變量噴霧實際應用已經(jīng)取得了較大的進展,在國外甚至已經(jīng)投入使用[21],但是依然存在電磁閥實際流量控制不十分精確,使得噴霧沉積量與噴霧需求量存在誤差。
一般情況下,電磁閥控的對靶噴霧需系統(tǒng)壓力穩(wěn)定,使得噴霧流量及噴霧特性可以被有效控制,但隨著精確對靶噴霧技術的發(fā)展,要求噴霧系統(tǒng)能根據(jù)作物有或無、大或小及各部位病害情況實時調節(jié)噴頭開啟數(shù)、噴頭開啟時間及流量大小進行按需施藥,這種各噴頭工作狀態(tài)的實時動態(tài)變化不僅會影響噴霧的總流量,也會改變系統(tǒng)壓力,從而反過來影響噴桿上各噴頭流量,而常規(guī)溢流裝置難以快速對這種動態(tài)的流量及壓力變化進行有效調整,因此動態(tài)條件下噴頭流量控制精確性不足。
為解決動態(tài)條件下電磁閥控對靶噴霧機噴霧流量不穩(wěn)定問題,本研究擬從研究動態(tài)條件下的電磁閥控噴霧流量特性著手,根據(jù)電磁閥控對靶噴霧機工作過程中所表現(xiàn)出的壓力及流量特征確定電磁閥控噴頭流量特性試驗參數(shù),通過試驗分析動態(tài)條件下各參數(shù)對電磁閥實際流量的影響,然后針對動態(tài)條件下影響對靶噴霧流量精確性的關鍵因素,利用神經(jīng)網(wǎng)絡算法進行動態(tài)條件下噴霧流量控制,驗證噴霧系統(tǒng)中電磁閥流量精準調節(jié)控制的可行性。本研究旨在明確電磁閥控對靶噴霧系統(tǒng)的流量特性,并完善其流量控制策略,以提高噴霧流量實時動態(tài)調節(jié)的精準度。
1 材料與方法
1.1 電磁閥控對靶噴霧機樣機
圖1為電磁閥控對靶噴霧機樣機,樣機包括4組噴桿,每組噴桿上3只噴頭。在進行噴頭開啟數(shù)變化條件下的噴霧試驗時,電磁閥的開啟數(shù)由紅外傳感器是否檢測到作物存在決定,試驗系統(tǒng)工作過程中,噴頭開啟數(shù)變化所導致的系統(tǒng)壓力變化由壓力傳感器讀出,通過該試驗可為下一步動態(tài)條件下的電磁閥控噴頭流量特性試驗限定動態(tài)壓力變化范圍。
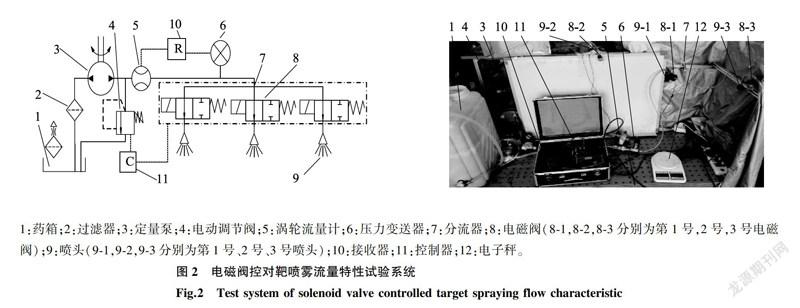
1.2 電磁閥控對靶噴霧流量特性試驗系統(tǒng)
為更好地進行噴頭開啟數(shù)、開啟時間、噴頭流量大小適時動態(tài)變化條件下的電磁閥流量試驗,在實驗室中搭建電磁閥控對靶噴霧流量特性試驗系統(tǒng),選用ZRHP-16C型電動調節(jié)閥,通過改變開口度調節(jié)流回藥箱的流量,大范圍調節(jié)系統(tǒng)壓力,模擬樣機中其他3只噴桿上噴頭啟閉及流量變化給該試驗噴桿帶來的壓力變化。選用LWGY-15型渦輪流量計進行總流量測量,各噴頭實際流量采用電子秤稱量,選用CYT-101型壓力變送器對壓力進行檢測。壓力信號及流量信號均通過基于52單片機的接收器讀出并記錄。選擇Airtac-2W系列直動常閉型高速電磁閥為對靶噴霧控制閥。試驗材料特征參數(shù)見表1。
藥液采用甘油水溶液進行模擬,259C時黏度為0.01Pa·s。定量泵(PLD1206型,4L/min,0.5MPa)將混合液送至噴桿處。由于不同的噴嘴類型,如扇形、圓形噴嘴僅對霧滴的沉積以及霧滴的物理特性影響較大,而對實際流量影響不夠顯著[17],因此僅選取農業(yè)中最常用的平面扇形噴頭進行噴霧試驗,噴頭為ARAG-422SF11005-04M型,額定工作壓力為0.4 MPa,流量為2L/min,滿足常規(guī)噴霧需求。
各電磁閥均通過獨立的脈沖輸出控制電路進行驅動,通過調節(jié)電磁閥的啟閉時間,即調節(jié)電磁閥脈沖占空比直接實現(xiàn)噴頭啟閉和開啟時間長短的控制,從而實際調節(jié)噴霧流量。控制器獨立脈沖輸出電路如圖3所示。MCU(STC89C52RC)實現(xiàn)各路脈沖信號的輸出,由DC5V驅動。外電路由DC12V驅動,通過光電耦合實現(xiàn)MCU電路與外電路的隔離,保護最小系統(tǒng)。外電路通過控制MOSFET(IRF840)進而控制電磁閥驅動電路的接通,電磁閥由DC24V驅動。
1.3 試驗方法
在電磁閥控對靶噴霧系統(tǒng)中,動態(tài)參數(shù)主要是系統(tǒng)壓力(P),此外還應包括電磁閥操作頻率(f)及占空比(D)。由于傳統(tǒng)噴霧機中依靠回流調壓的方式易造成系統(tǒng)壓力調節(jié)滯后及不準確,因此未來的電磁閥控噴霧系統(tǒng)可采用計量泵供給實現(xiàn)主動的噴霧總流控制方式,而各電磁閥則適時調節(jié)控制參數(shù)以滿足精準噴霧需求。根據(jù)圖1樣機試驗結果中噴頭開啟數(shù)變化導致的噴霧壓力波動范圍,樣機所有噴桿上僅有數(shù)只噴頭工作時系統(tǒng)壓力高達0.35Mpa,而當所有噴頭均打開時,由于系統(tǒng)供流不足,系統(tǒng)壓力低至0.09Mpa。因此電磁閥控對靶噴霧流量特性試驗中動態(tài)條件下噴桿壓力區(qū)間定為0.10~0.35MPa,以模擬樣機的工作狀態(tài),該噴霧壓力范圍低壓部分不滿足正常噴霧需求,但考慮到實際對靶噴霧機出現(xiàn)的極端情況,足以用于研究動態(tài)條件下電磁閥控對靶噴霧的流量特性。而在未來實際的對靶噴霧機中系統(tǒng)供流應與所需噴霧量一致。
試驗中共3只電磁閥及外接噴頭裝在同一噴桿上,僅依靠電磁閥的完全啟閉難以實現(xiàn)0.10~0.35 MPa的壓力調節(jié),因此采用電動調節(jié)閥模擬調節(jié)樣機其他噴桿_上的壓力變化,1號、2號電磁閥則用于模擬該噴桿上受噴頭開啟數(shù)、開啟時間影響所帶來的系統(tǒng)壓力變化,同時,當3號電磁閥由于流量改變導致系統(tǒng)壓力變化時,通過1號、2號電磁閥進行壓力調節(jié),從而滿足一定壓力條件下3號電磁閥實際流量的測試,即電動調節(jié)閥與1號、2號電磁閥二者配合調節(jié)系統(tǒng)壓力到測試壓力(P)點上。試驗系統(tǒng)動態(tài)壓力調節(jié)如表2所示。
為了測試3號電磁閥動態(tài)條件下的流量特性,控制3號電磁閥實際操作參數(shù)f為6Hz、8Hz、10Hz、12Hz、14Hz、16Hz、18Hz、20Hz,D為10%、20%、30%、40%、50%、60%、70%、80%、90%、100%,對該控制參數(shù)下3號電磁閥的實際流量進行測量。重復試驗,取3號電磁閥流量均值作為特征流量。
2 結果與分析
2.1 動態(tài)變化條件下電磁閥流量
將3號電磁閥在同一工作參數(shù)下重復試驗所得實際流量均值作為該控制參數(shù)(Pf、D)下的電磁閥實際流量特征,用以分析實際電磁閥控對靶噴霧中動態(tài)變化條件下的流量特性。不同P、f、D條件下電磁閥實際流量Q試驗結果如圖4所示。定義流量控制線性區(qū)間(Linear interval)為:能夠采用線性擬合方法將一定P及f條件下的Q與D進行線性擬合的D的區(qū)間。因此線性區(qū)間越大則意味著能夠以線性特征進行流量控制的范圍越廣,流量調節(jié)分辨率越高。
在線性區(qū)間內,P不變時,Q可以通過調節(jié)D實現(xiàn)較為精確的控制,而在線性區(qū)間外Q_D關系則無法用線性區(qū)間內的線性關系進行擬合。且當D超出線性區(qū)間后,隨著D的提高,Q基本不再進一步提高,即電磁閥可視為處于常開狀態(tài),Q無法進一步控制。
在任-P條件下,不同的f會影響線性區(qū)間的大小。隨著f的增加,線性區(qū)間均呈現(xiàn)逐漸減小的趨勢,如8Hz時,不同P的線性區(qū)間均為0.8(0.10~0.90),而在20Hz時,線性區(qū)間范圍僅為0.30~0.60,這意味著增大f會降低Q控制的精度。與線性區(qū)間變化規(guī)律不同的是,隨著f的改變,Q調節(jié)范圍并不會產(chǎn)生明顯變化。但是不同f下,不同的D所對應的輸出流量Q卻存在差異。
P變化對Q影響顯著,隨著P的增大,電磁閥最大流量呈現(xiàn)逐漸增高的趨勢,不同f條件下從P=0.10MPa時約600 ml/min逐漸提高到P=0.35 Mpa時的約1700ml/min,可見P變化對電磁閥實際流量影響顯著,在試驗條件下,P每提高0.05 MPa,Q提高約200ml/min,因此在實際的電磁閥控對靶噴霧系統(tǒng)中,需要考慮P的波動對單噴頭實際Q值的影響。
2.2 動態(tài)變化條件下電磁閥流量BP神經(jīng)網(wǎng)絡控制
傳統(tǒng)電磁閥控制流量的方式是僅調節(jié)D實現(xiàn)變量噴霧,但是這種策略因實際工作中動態(tài)工作狀況的存在,以及常規(guī)溢流裝置無法實現(xiàn)及時穩(wěn)壓,實際噴霧流量誤差較大。由于電磁閥控對靶噴霧中的實際Q與P、D以及f三者間存在非線性關系,因此可綜合電磁閥控制參數(shù)D、f以及動態(tài)條件下的P實現(xiàn)對Q的精準調節(jié)。針對非線性問題,需要選取合適的控制方法,BP神經(jīng)網(wǎng)絡曾被用于變量噴霧系統(tǒng)中的供藥系統(tǒng)流量的精確控制222,其具有較強的非線性映射能力以及較高的容錯能力,因此滿足用于驗證動態(tài)條件下電磁閥控對靶噴霧流量精準控制的條件。
2.2.1 BP神經(jīng)網(wǎng)絡數(shù)據(jù)輸入與模型訓練針對電磁閥實際流量的控制,采用3層BP神經(jīng)網(wǎng)絡結構對試驗數(shù)據(jù)進行訓練檢驗。BP神經(jīng)網(wǎng)絡輸入量為PD和f,輸出量為Q。神經(jīng)網(wǎng)絡的應用中,隱含層節(jié)點數(shù)的選擇需要根據(jù)數(shù)據(jù)擬合的精度來選擇,隱含層節(jié)點數(shù)可表示為:
公式
N為輸入層節(jié)點數(shù),0為輸出層節(jié)點數(shù),M為小于10的任意正整數(shù)。
因此,該BP神經(jīng)網(wǎng)絡隱含層選擇為5個節(jié)點,輸入層3個節(jié)點,輸出層1個節(jié)點。3層神經(jīng)網(wǎng)絡的表達式可表示為:
公式
式中,X;為輸入量,分別代表系統(tǒng)壓力(P)、電磁閥占空比(D)以及電磁閥頻率(f);y;為隱層輸出;i和j分別為輸入層和隱層節(jié)點個數(shù);Zx為輸出量,即電磁閥的實際輸出流量;W表示連接權重,C,b表示偏差。
BP神經(jīng)網(wǎng)絡隱含層常采用Sigmoid傳輸函數(shù),且BP神經(jīng)網(wǎng)絡的輸入層到隱含層采用Sigmoid函數(shù)的雙曲正切Tansig作為傳輸函數(shù)時,比采用對數(shù)函數(shù)Logsig網(wǎng)絡帶來的誤差小,輸出層常采用Purelin函數(shù)用于模式識別241。本模型驗證中BP神經(jīng)網(wǎng)絡的神經(jīng)元傳遞函數(shù)采用S型正切函數(shù)Tansig,輸出層則采用線性函數(shù)Purelin作為神經(jīng)元傳遞函數(shù)。
由于實際流量同電磁閥各控制參數(shù)間存在一定范圍內的線性關系,因此訓練前需對3個動態(tài)變量下共480組數(shù)據(jù)的編號進行隨機排序,以減小訓練誤差,其中80%數(shù)據(jù)用于模型訓練,20%數(shù)據(jù)用于模型驗證。對輸入訓練樣本數(shù)據(jù)以及測試樣本數(shù)據(jù)均使用Mapminmax函數(shù)進行歸一化處理以消除量綱影響,提高網(wǎng)絡收斂性能。
2.2.2 BP神經(jīng)網(wǎng)絡的遺傳算法優(yōu)化由于采用BP神經(jīng)網(wǎng)絡進行預測容易存在精確性不足的問題,且難以滿足實際控制需求[23],因此提出對BP神經(jīng)網(wǎng)絡進行優(yōu)化,驗證進一步提高動態(tài)條件下噴霧流量控制精確性的可行性。遺傳算法是模擬自然界遺傳機制和生物進化論而成的一種并行隨機搜索最優(yōu)化方法。遺傳算法應用于BP神經(jīng)網(wǎng)絡的目的是優(yōu)化其初始權值和閾值,且理論上認為使用優(yōu)化后的網(wǎng)絡[25]預測的精確性更好。
首先進行種群初始化,然后根據(jù)個體得到BP神經(jīng)網(wǎng)絡的初始權值和閾值,用訓練數(shù)據(jù)訓練BP神經(jīng)網(wǎng)絡后預測系統(tǒng)輸出。預測輸出和期望的輸出之間的誤差絕對值之和作為個體適應度值F,計算公式為:
公式
式中,abs為絕對值函數(shù);n為網(wǎng)絡輸出節(jié)點數(shù);y;為BP神經(jīng)網(wǎng)絡第i個節(jié)點的期望輸出,0;為第i個節(jié)點的實際輸出;k為系數(shù)。
選擇輪盤賭法進行遺傳算法選擇操作,即基于適應度比例的選擇策略,每個個體i的選擇概率P為:
公式
式中,N為種群個體數(shù)目;m為系數(shù)。
采用實數(shù)交叉法進行交叉操作,第k個染色體ap和第l個染色體a,在交叉位j的操作可寫為:
公式
變異操作:
公式
式中,r2是一個隨機數(shù);g為當前迭代次數(shù);G'max是最大的進化次數(shù);本試驗中取最大迭代次數(shù)為10次。r為[0,1]間的隨機數(shù)。
2.2.3 基于神經(jīng)網(wǎng)絡的電磁閥流量控制模型測試及結果分析采用BP神經(jīng)網(wǎng)絡以及遺傳算法優(yōu)化的BP神經(jīng)網(wǎng)絡訓練結果如圖5所示。圖5A為BP網(wǎng)格訓練性能,均方誤差收斂于0.0086507,收斂良好;圖5B顯示優(yōu)化算法訓練的均方誤差收斂于0.0068377,稍優(yōu)于BP神經(jīng)網(wǎng)絡算法。圖6A,圖6B顯示兩算法均具有較高的擬合準確性。
使用神經(jīng)網(wǎng)絡進行模型的預測存在著誤差,誤差的大小說明了使用該模型進行流量控制的精確性。使用平均誤差比例E,衡量這一指標。
公式
式中n為測試樣本數(shù),QR為電磁閥實際流量輸出,Q,為神經(jīng)網(wǎng)絡理論輸出。BP神經(jīng)網(wǎng)絡控制誤差為0.183,遺傳算法優(yōu)化的BP神經(jīng)網(wǎng)絡算法控制誤差為0.151,2種控制方法誤差在可接受范圍內,均具有較高精度。部分存在較大誤差的數(shù)據(jù)是由于試驗精度導致的,未來通過使用更為精密的噴霧控制設備,可以達到更高的噴霧流量控制精度。
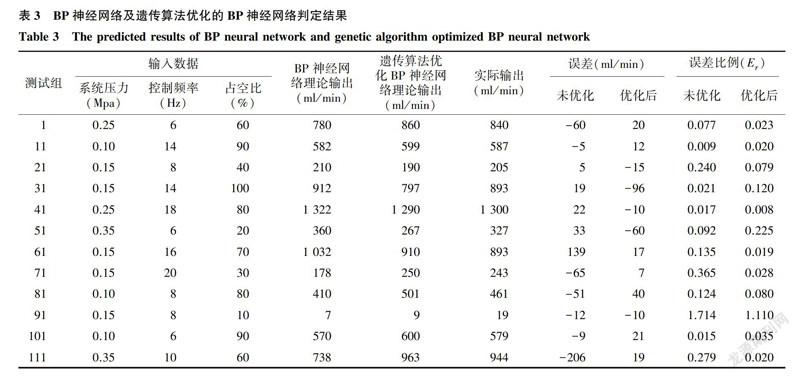
表3給出了部分采用BP神經(jīng)網(wǎng)絡及遺傳算法優(yōu)化的BP神經(jīng)網(wǎng)絡驗證樣本測試結果。可見優(yōu)化的BP神經(jīng)網(wǎng)絡具有更高的精度,只有極個別低流量數(shù)據(jù)存在較大誤差。
因此,依靠神經(jīng)網(wǎng)絡進行動態(tài)條件下電磁閥流量的精準控制可行,且采用遺傳算法優(yōu)化的BP神經(jīng)網(wǎng)絡模型能夠達到更高的控制精度,能夠應用于動態(tài)下噴桿上各電磁閥實際流量的有效控制。試驗結果中存在的誤差未來可隨著試驗數(shù)據(jù)量的加大,元件精度的提升得到進一步解決。
3 結論
本研究針對電磁閥控對靶噴霧機實際作業(yè)中在動態(tài)條件下噴霧流量控制不精確的問題,研究了電磁閥控對靶噴霧流量特性,并提出采用BP神經(jīng)網(wǎng)絡,將P,D以及f同時作為控制參數(shù)進行動態(tài)條件下的精準Q控制的策略。試驗結果表明,線性區(qū)間(I)內依靠調節(jié)D可以實現(xiàn)Q較為精準的調節(jié);f主要影響I大小,隨著f的升高,1收窄,基于D進行Q調節(jié)的精度下降,P及D不變時調節(jié)f也可以實現(xiàn)對Q的調節(jié)。
P對Q調節(jié)范圍影響顯著,試驗條件下P每增大0.05MPa,Q的最大調節(jié)范圍增加約200ml/min。因此,考慮到對靶噴霧機動態(tài)工作時P存在變化,且常規(guī)溢流裝置對P的穩(wěn)定效果欠缺,在電磁閥控對靶噴霧系統(tǒng)實際應用中,要解決動態(tài)條件下精準流量控制問題,P應該作為電磁閥控對靶噴霧流量控制參數(shù)之一,以實現(xiàn)對實際噴霧流量的進一步精準控制。
驗證結果表明基于BP神經(jīng)網(wǎng)絡的流量控制模型能夠精準地進行動態(tài)條件下電磁閥流量的控制,BP神經(jīng)網(wǎng)絡預測誤差比例(E)在0.2以內,遺傳算法進行優(yōu)化的BP神經(jīng)網(wǎng)絡控制算法相比單純BP神經(jīng)網(wǎng)絡具有更高的控制精度(E)達到0.15。實際動態(tài)條件下,在電磁閥控對靶噴霧流量控制中,除了將D作為控制參數(shù)以外,通過將P以及f同時作為控制參數(shù),可以進行噴頭開啟數(shù)、開啟時間、流量大小適時變化條件下噴桿上各電磁閥實際流量的有效控制,從而解決動態(tài)條件下電磁閥控對靶噴霧流量的精準控制問題。
參考文獻:
[1]邱白晶,閆潤,馬靖,等.變量噴霧技術研究進展分析[J].農業(yè)機械學報,2015,46(3):59-72.
[2]薛新宇,蘭玉彬.美國農業(yè)航空技術現(xiàn)狀和發(fā)展趨勢分析[J].農業(yè)機械學報,2013,44(5):194-201.
[3]鄭加強,周宏平,徐幼林,等.農藥精確對靶施用及其系統(tǒng)設計[J].農業(yè)工程學報,2005,21(11):67-72.
[4]張美娜,呂曉蘭,雷嘵暉.可移植的對靶噴霧控制系統(tǒng)設計與試驗[J].江蘇農業(yè)學報,2017,33(5):1182-1187.
[5]ZHU H,OZKAN H E,BRAZEE R D,et al.A system to determine lag time and mixture uniformity for inline injection sprayers[J].Applied Engineering in Agriculture,1998,14(2):103-110.
[6]LUCK J D,SHEARERS,LUCK B D,et al.Recalibration methodology to compensate for changing fluid properties in an individualnozzle direct injection system[J].Transactions of the ASABE,2016,59(3):847-859.
[7]VONDRICKA J,LAMMERS P s.Evaluation of a carrier control valve for a direct nozzle injection system[J].Biosystems Engineering,2009,103(1):43-48.
[8]鄒凡,肖茂華,傅秀清,等.新型南方水田噴桿噴霧機液壓系統(tǒng)的設計與分析[J].江蘇農業(yè)學報,2018,34(1):220-224.
[9]鄧巍,何雄奎,丁為民.基于壓力變量噴霧的霧化特性及其比較[J].江蘇大學學報(自然科學版),2009,30(6):545-548.
[10]ZHU H,0ZKAN H E,F(xiàn)OX R D,et al.Mixture uniformity in supply lines and spray patterns of a laboratory injection sprayer[J].Transactions of the ASAE,1998,14(3):223-230.
[1]VONDRICKA J,LAMMERS P s.Evaluation of a carrier control valve for a direct nozzle injection system[J].Biosystems Engineer-ing,2009,103(1):43-48.
[12]HLOBEN P.Study on the response time of direct injection systems for variable rate application of herbicides[D].Bonn:University of Bonn,2007.
[13]CHEN Y,ZHU H,0ZKAN H E.Development of a variable-rate sprayer with laser scanning sensor to synchronize spray outputs to tree structures[J].Transactions of the ASABE,2012,55(3):773-781.
[14]LIU H,ZHU H,SHEN Y,et al.Development of digital flow control system for multi-channel variable-rate sprayers[J].Transactions of the ASABE,2014,57(1):273-281.
[15]吳春篤,杜彥生,張偉,等.脈寬調制型變量噴霧系統(tǒng)霧量沉積分布[J].農業(yè)機械學報,2007,38(12):70-73.
[16]鄧巍,丁為民.基于PWM技術的連續(xù)式變量噴霧裝置設計與特性分析[J].農業(yè)機械學報,2008,39(6):77-80.
[17]翟長遠,王秀,密雅榮,等.PWM變量噴霧噴頭流量模型[J].農業(yè)機械學報,2012,43(4):40-44.
[18]魏新華,蔣杉,孫宏偉,等.PWM間歇噴霧式變量噴施控制器設計與測試[J].農業(yè)機械學報,2012,43(12):87-93.
[19]蔣煥煜,周鳴川,童俊華,等.基于卡爾曼濾波的PWM變量噴霧控制研究[J].農業(yè)機械學報,2014,45(10):60-65.
[20]李龍龍,何雄奎,宋堅利,等.基于高頻電磁閥的脈寬調制變量噴頭噴霧特性[J].農業(yè)工程學報,2016,32(1):97-103.
[21]SHEN Y,ZHU H.Embedded computer controlled premixing in-line injection system for air-assisted variable-rate sprayers[J].Transactions of the ASABE,2015,58(1):39-46.
[22]張敏,范龍,代祥,等.基于BP神經(jīng)網(wǎng)絡的變量噴霧供藥系統(tǒng)研究[J].林業(yè)工程學報,2017,2(2):133-137.
[23]李晉陽,賈衛(wèi)東,魏新華.基于流量調節(jié)閥和神經(jīng)網(wǎng)絡的植保機械在線混藥裝置[J].農業(yè)機械學報,2014,45(11):98-103.
[24]蒲春,孫政順,趙世敏.Matlab神經(jīng)網(wǎng)絡工具箱BP算法比較[J].計算機仿真,2006,23(5):142-144.
[25]田亮,羅宇,王陽.基于遺傳算法優(yōu)化BP神經(jīng)網(wǎng)絡的TIG焊縫尺寸預測模型[J].上海交通大學學報(自然科學版),2013,47(11):1690-1696.

