三維葉盤失諧模態分析的攝動降階方法

周子宣,徐自力

(1.西安交通大學機械結構強度與振動國家重點實驗室,710049,西安;2.西安交通大學航天航空學院,710049,西安)

理想情況下,整體葉片輪盤具有循環對稱性,并且每個扇區具有相同的幾何形狀和材料特性,因此可利用單個扇區的模型計算整體葉盤系統結構振動特性。然而,各個扇區的結構特性會由于制造公差、運行磨損等因素引入偏差,這種偏差稱為失諧,失諧會導致振動能量集中和強迫振動響應幅值的急劇增加[1-2]。因此,在葉盤設計過程中,須考慮失諧的影響,以防止由于結構高周疲勞引起的失效。早期失諧葉盤的研究主要利用集中參數模型和連續參數模型[3-4],分析結構參數對局部化程度的影響規律,但模型過于簡化,無法直接對應較為復雜的葉片輪盤結構。隨著計算機硬件的發展,逐漸利用三維實體有限元模型對輪盤結構進行分析[5]。Kan等利用完整有限元模型分析了Rotor#67失諧葉盤在科氏力作用下的響應特征[6],但由于復雜葉盤整體有限元模型包含大量自由度,對其進行完整計算分析需耗費大量資源,計算效率較低。

因此,有學者開發了各種降階模型[7-9],在準確預測失諧葉盤振動特性的同時顯著減少計算量。Bhartiya等利用降階模型,從統計學角度給出了失諧分布與失諧頻率之間的對應關系,但其簡化程度較高,不適合針對復雜模型進行精確分析[10]。Madden等深入討論了CMM方法中各參數對求解精度的影響[11]。徐自力等利用多重模態降階方法對大型復雜葉盤轉子結構進行了模態求解,與實驗結果基本一致,具有較高的精度[12]。

由于失諧量是隨機產生的,需要計算多種不同失諧分布情況下的葉盤模態,從而最大限度預測葉盤最危險的振動情況。利用常規有限元降階方法能在一定程度上提高計算效率,但在失諧分布情況發生變化后,需對葉盤整體重新進行降階并求解特征值,計算多種失諧分布下葉盤模態的時間成本仍然巨大。

本文提出了一種攝動降階方法,該方法將失諧葉盤分為諧調部分與失諧部分,利用單次降階結果,結合不同的失諧改變量,通過攝動方法將模態求解轉化為攝動量與諧調矩陣乘積形式,省去了常規降階方法中重新降階與求解環節,從而提高了計算效率。

1 降階方法

諧調葉盤周向各葉片與對應的輪盤滿足循環對稱特征,為降低模型處理的復雜程度,將相鄰兩只葉片的中心分割面作為扇區邊界,劃分得到若干幾何形狀相同的扇區。將葉盤扇區作為基本子結構可避免對形式相同的扇區質量剛度矩陣重復降階,從而提高計算效率。

對單個葉片扇區采用固定界面模態綜合法[13]進行降階,子結構的原始振動微分方程為

(1)

式中:M為子結構質量矩陣;K為子結構剛度矩陣;f為子結構界面力矩陣。

將運動方程中的剛度矩陣、質量矩陣和界面力按子結構內部和對接界面自由度分塊,則運動微分方程可寫為

(2)

式中:uI為需縮減的內部節點自由度;uF為子結構對接界面自由度;f為子結構的界面力。

采用固定界面模態綜合法時,將子結構內部任意節點位移表示為界面固定時的節點位移與界面位移相對節點的牽連位移之和,即

(3)

式中:Ψn為界面節點固定時的主模態;Ψc為界面發生位移后的約束模態;n為主模態數目;nf為約束模態數目。由主模態與約束模態定義可得

(KII-ΛMII)Ψn=0

(4)

Ψc=-KII-1KIF

(5)

式中Λ為子結構特征值對角陣。

在結構振動分析中,由于只關注小部分低階次的主模態,在此選取主模態Ψn的前k階Ψk,則子結構內部節點位移的降階關系可表示為

(6)

式中T稱為降階轉換矩陣。將式(6)代入式(2)并左乘TT,可得

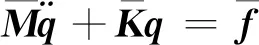
(7)

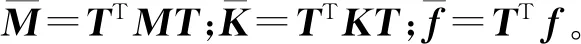
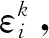
(8)

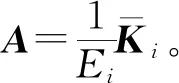
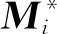
(9)

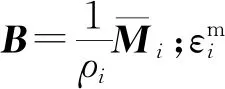
對剛度陣和質量陣,可利用式(6)中的轉換矩陣進行重新降階,得到廣義坐標下帶有失諧改變量的子結構振動微分方程

(10)

葉盤中將每個扇區作為一個子結構,系統的子結構與葉片數目N相同,對接形式如圖1所示。根據位移協調條件,第i個子結構的左界面與第i+1個子結構的右界面位移一致;根據力平衡條件,第i個子結構的左界面力與第i+1個子結構的右界面力之和為0。由N個子結構組成的整體葉盤振動微分方程可表示為

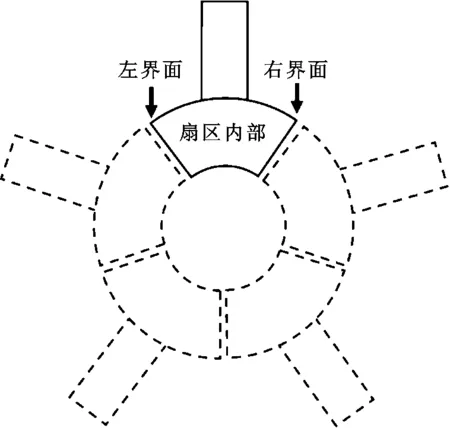
圖1 葉盤扇區對接示意

(11)

式中

(12)

(13)

為方便級數展開,將多個子結構失諧量矩陣構成的整體失諧改變矩陣統一表示為一小參數ε*與矩陣乘積的形式

(14)

(15)

(16)

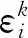
(17)

式中:Φp、Λp分別為失諧葉盤特征向量、特征值矩陣。將第i階失諧模態振型與頻率按ε*進行展開。由于葉盤失諧為小量,保留ε*的1次項進行近似計算,即

(18)

(19)

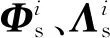
將式(18)(19)代入式(17),利用待定系數法,等式兩端ε的1次項系數應相等,即

(20)

整理得

(21)

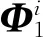
(22)

式中:Cj為對應項系數;ns為截取的諧調模態振型數量。

(23)

當i≠j時,利用正交振型規范條件可得

(24)

當i=j時,利用正交振型規范條件可得

(25)

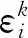
2 失諧葉盤模態計算

以NASA Rotor#67葉盤[14]為研究對象,采用攝動降階法對失諧葉盤進行模態分析。葉盤整體結構如圖2所示,葉盤整體結構共包含22個葉片扇區,每個扇區自由度為5.8萬,整個葉盤自由度為128萬。

圖2 失諧葉盤整體結構

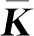
而在利用常規降階方法(模態綜合法)計算失諧葉盤模態時,計算按照圖3右側流程進行,在計算不同失諧分布情況下的葉盤模態時,需要重新定義失諧量并進行降階。得到整體失諧矩陣后,再進行完整的特征值求解過程。攝動方法的優勢在于利用了已有的諧調葉盤模態結果,只需考慮變化的失諧部分,將失諧頻率與振型轉化為式(21)、式(25)的矩陣乘積形式,計算速度高于完整矩陣特征值求解過程的速度,有效提高了失諧葉盤模態計算效率。

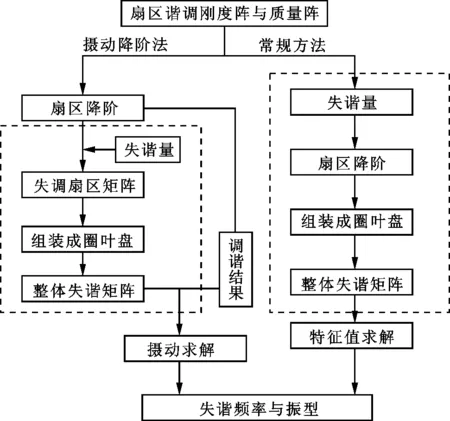
圖3 攝動降階方法與常規計算方法流程對比

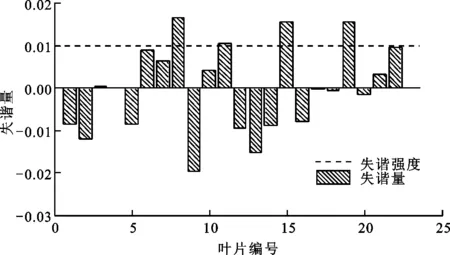
圖4 隨機失諧量分布情況

隨機失諧量分布情況如圖4所示,設定保留的模態階次Ψk為100。利用攝動降階法計算得到了該葉盤前100階固有頻率,對于同樣模型,分別利用完整非降階方法與模態綜合法計算得到失諧葉盤的相同階次固有頻率,3種計算結果如圖5所示,可知攝動降階法的計算結果與完整法計算結果相吻合,葉盤頻率分布呈現明顯的階梯特征,不同階梯處分別對應不同的葉片振動階次,在各個階梯之間存在若干個葉片與輪盤相互耦合的過渡模態。

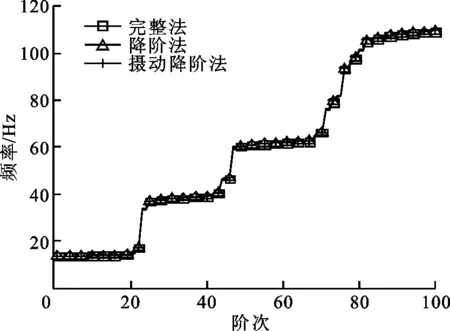
圖5 葉盤前100階模態頻率分布

以完整法計算結果為基準,分別作出常規降階方法與攝動降階法計算前100階模態頻率的相對誤差,固有頻率計算相對誤差隨失諧強度σ的變化如圖6所示。由圖6可知:失諧強度為0.01時,攝動降階法對固有頻率的計算誤差可以保持在0.25%以下;失諧強度增大至0.02后,攝動降階法計算誤差出現一定波動,大部分頻率的計算誤差仍維持在0.3%以下;失諧強度為0.03時,根據統計學原理,失諧量最大將達到6%,葉片間剛度的誤差已達到極端值,實際工況下已很難發生,誤差仍控制在0.3%左右,說明該算法在失諧強度為0.03以內時具有較好的精度穩定性。

失諧強度為0.01時分別統計了3種方法計算前100階模態的耗時,如表1所示。當Ψk取為100時,完整法計算時間為320 s;常規降階法計算時間為34.5 s,約為完整法計算時間的9.4%;攝動降階法計算時間為11.2 s,約為完整法的3.5%。常規降階法采用完整矩陣特征值來求解,而攝動降階法采用失諧矩陣與諧調矩陣乘積的形式計算特征值,其計算效率高于常規降階法。

當Ψk數目由100增至800時,利用常規降階方法計算時,特征值求解的時間復雜度為O(n3)[15],降階整體矩陣維度變為原來的8倍,計算時間將顯著增加,總耗時由34.5 s增至185.2 s。攝動降階法僅計算振型向量與矩陣的乘積,計算復雜度為O(n2),計算耗時相對于常規降階法大大降低,總耗時僅由11.2 s增至24.2 s。攝動降階法在較高的主模態數目下,計算失諧葉盤固有頻率仍具有較高的效率。

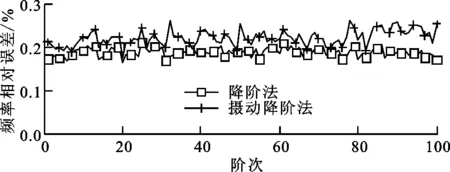
(a)σ=0.01

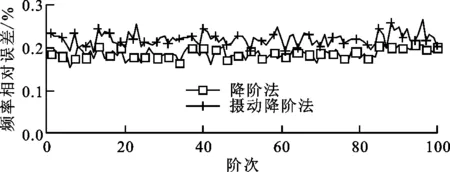
(b)σ=0.02

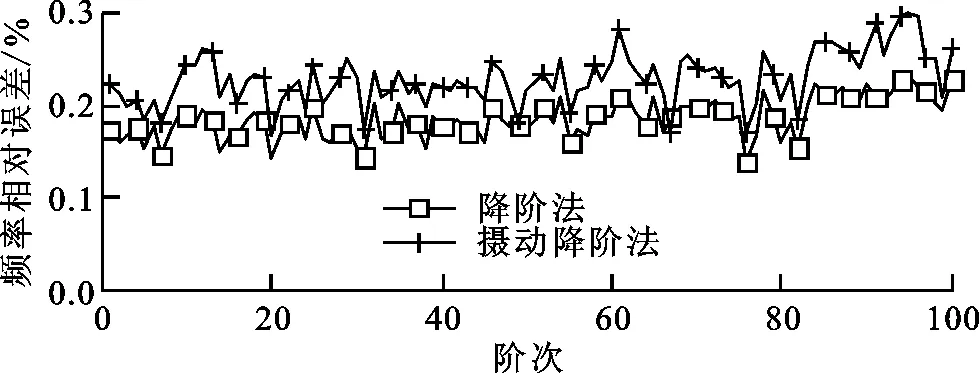
(c)σ=0.03圖6 固有頻率計算相對誤差隨失諧強度的變化

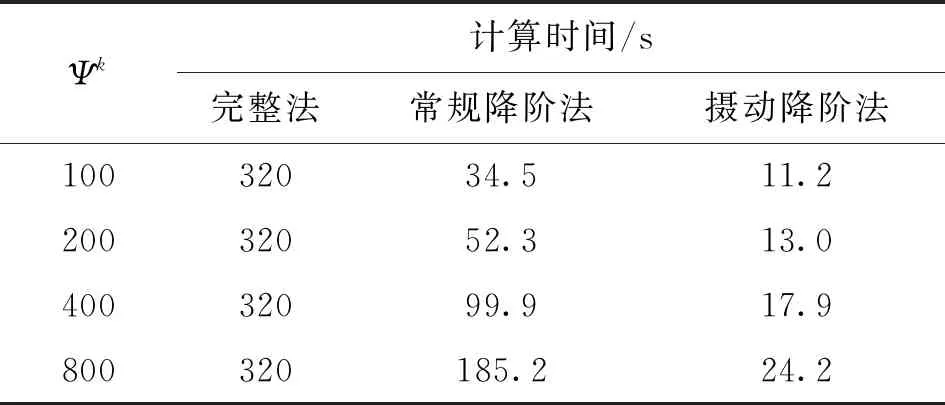
Ψk計算時間/s完整法常規降階法攝動降階法10032034.511.220032052.313.040032099.917.9800320185.224.2

進一步討論保留主模態階數對計算精度的影響,失諧強度為0.01時,將保留的主模態階數分別增至200、400后,再次對比了攝動降階法與常規降階法的計算誤差,如圖7所示。當k=200時,攝動降階法的計算誤差波動程度較圖6b降低至0.2%以下。提高Ψk數至400,攝動降階方法計算誤差進一步降至0.15%以下。較多主模態數可以保留更多的子結構振型信息,攝動降階法利用該部分原始數據對失諧結構進行求解,故提高Ψk數可顯著降低攝動降階法的計算誤差。考慮整體前100階模態可滿足分析需求,保留主模態Ψk數為整體模態數目的4倍時,即可保證較高的計算精度。

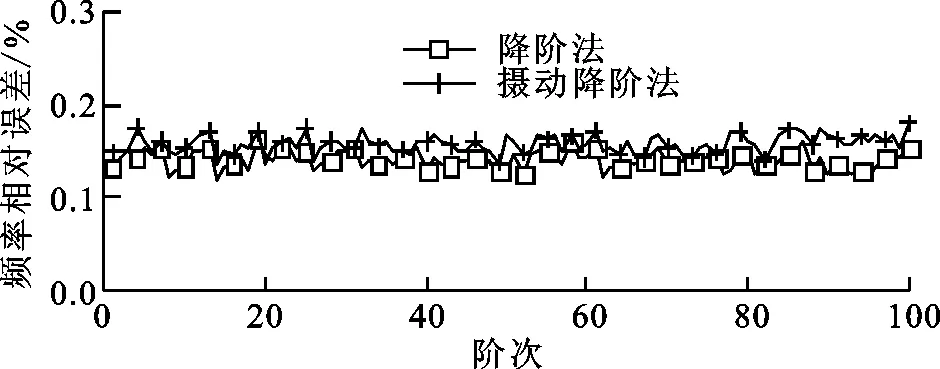
(a)Ψk=200

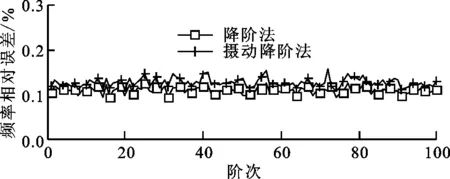
(b)Ψk=400圖7 各階模態頻率計算相對誤差隨Ψk數的變化

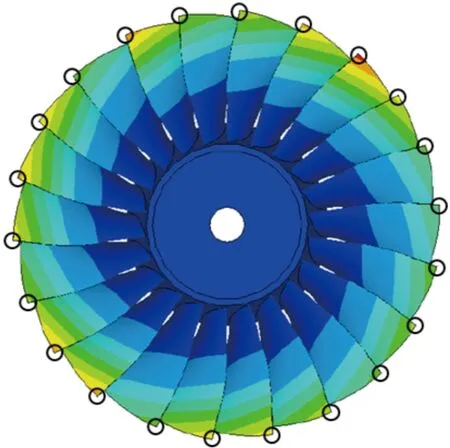
圖8 完整法第2階模態位移云圖與葉尖節點位置示意

為突出失諧特征對振型的影響,取各葉片葉尖處節點位移進行討論,節點位置如圖8所示。將22只葉片按照順時針順序依次編號為1～22,分別提取完整法與攝動降階法計算得到的葉盤第2階與第3階模態中葉尖相同位置的模態位移,不同階次下攝動降階方法模態位移計算結果圖9所示,可知攝動降階方法計算結果與完整法的結果吻合,葉盤發生失諧后,相鄰葉尖模態位移出現突變,發生了模態局部化現象。

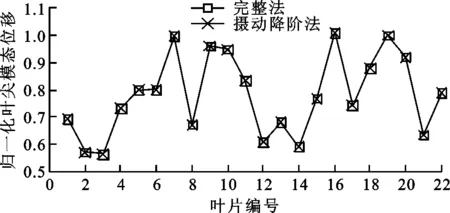
(a)階次為2

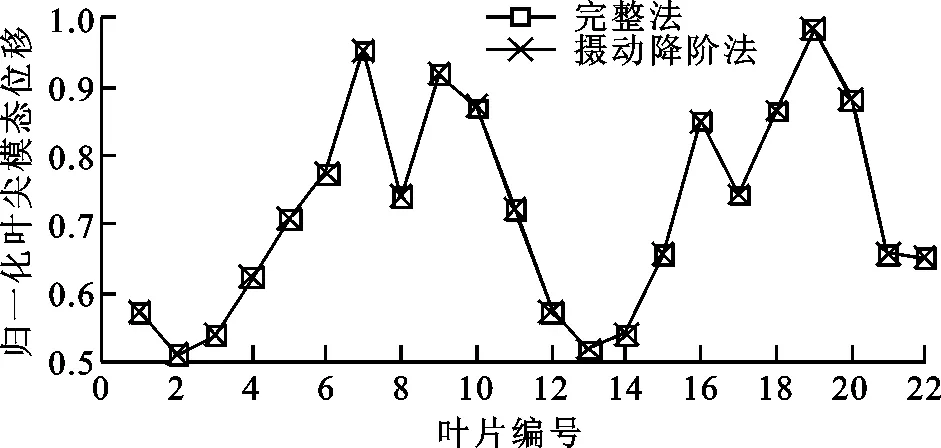
(b)階次為3圖9 不同階次下攝動降階方法模態位移計算結果

保持失諧強度為0.03,統計了第7、14、21只葉片葉尖前100階歸一化模態位移的計算誤差,葉尖節點歸一化模態位移計算誤差如圖10所示,可知計算誤差基本小于0.25%,其中第20、40、70階左右計算誤差波動較為明顯。對比圖5可知,該模態階次屬于葉片輪盤耦合過渡模態,此時耦合作用使振動的非線性性質顯著,而攝動方法以線性展開逼近精確解,此區域的計算誤差有所波動,但總體依然保持在0.25%以下,滿足工程計算精度要求。

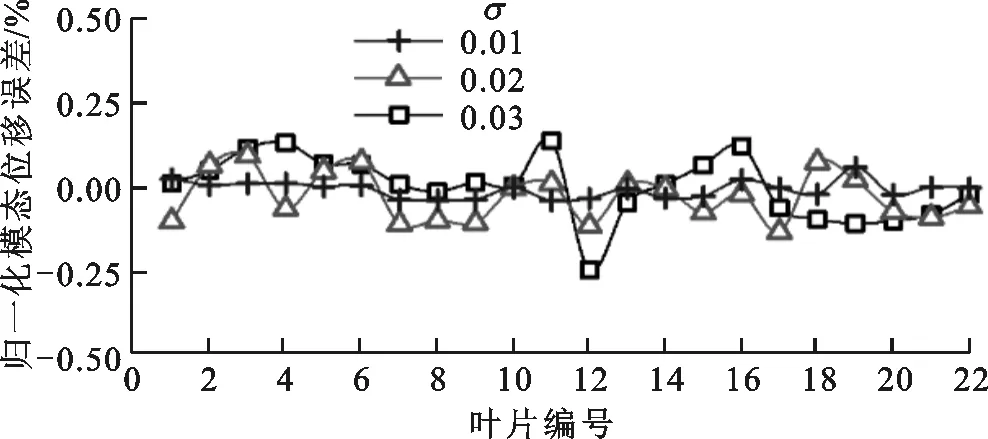
(a)階次為22

(b)σ=0.03圖10 葉尖節點歸一化模態位移計算誤差

3 結 論

本文提出了一種用于計算失諧葉盤模態的攝動降階方法,以Rotor#67葉盤作為算例進行驗證。在隨機失諧強度為0.01時,攝動降階方法對前100階頻率計算誤差在0.15%以下,失諧強度增加至0.03后,固有頻率的計算誤差低于0.3%,葉尖模態位移的計算誤差低于0.25%,具有較高的精度穩定性。保留的主模態階數為整體模態數目的4倍時,可保證較高的計算精度。在計算效率方面,主模態數為100時,攝動降階方法計算時間僅為常規降階法計算時間的30%。分析復雜結構葉盤在多種不同失諧分布形式下的振動特征時,攝動降階法可加快葉盤固有頻率與振型的計算速度。

本文方法主要針對單級葉盤進行分析,后續可在本方法基礎上針對多級葉盤軸耦合結構開發出面向多部件系統的攝動降階方法,考慮各部件之間的相互影響,從而更加精確地分析失諧葉盤轉子系統的動力學特性。