初中數(shù)學(xué)建模教學(xué)研究

林子植 　胡典順

摘要：在初中學(xué)段開展數(shù)學(xué)建模活動，面臨巨大的困難和挑戰(zhàn)。而PISA數(shù)學(xué)素養(yǎng)評價框架以數(shù)學(xué)建模周期理論為基石，提出數(shù)學(xué)建模周期包含三個過程：建模、應(yīng)用和闡釋。一道PISA試題只考查其中的一個過程。初中數(shù)學(xué)建模教學(xué)可以借鑒這種“分而治之”的思想，規(guī)劃數(shù)學(xué)建模能力的培養(yǎng)路徑，尋找數(shù)學(xué)建模任務(wù)的設(shè)計依據(jù)，確立數(shù)學(xué)建模能力的評價維度。

關(guān)鍵詞：數(shù)學(xué)建模教學(xué) PISA 數(shù)學(xué)建模周期理論

《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版）》將數(shù)學(xué)建模定義為“對現(xiàn)實問題進行數(shù)學(xué)抽象，用數(shù)學(xué)語言表達問題、用數(shù)學(xué)方法構(gòu)建模型解決問題”，并建議以課題研究的形式開展數(shù)學(xué)建模活動，讓學(xué)生經(jīng)歷“實際情境—提出問題—建立模型—求解模型—模型檢驗—實際結(jié)果”的過程，最終以研究報告或者小論文的形式呈現(xiàn)數(shù)學(xué)建模過程。但是，應(yīng)用數(shù)學(xué)知識、技能解決一個真實的情境問題，完整地經(jīng)歷上述數(shù)學(xué)建模過程，不僅需要具備較高的數(shù)學(xué)認(rèn)知水平，還需要耗費較長的時間。初中生的數(shù)學(xué)認(rèn)知水平還處于初等層次，再加上基礎(chǔ)教育階段學(xué)業(yè)負擔(dān)較重，很難騰出專門的課程時間來安排數(shù)學(xué)建模活動。因此，在初中學(xué)段開展數(shù)學(xué)建模活動，面臨巨大的困難和挑戰(zhàn)。所以，在初中學(xué)段，設(shè)計什么樣的數(shù)學(xué)建模任務(wù)來開展數(shù)學(xué)建模活動，怎樣在日常教學(xué)過程中開展數(shù)學(xué)建模教學(xué)，是值得研究和討論的課題。

PISA作為廣受認(rèn)可的國際學(xué)生評估項目，在評估學(xué)生的數(shù)學(xué)素養(yǎng)時，主張測量學(xué)生應(yīng)用數(shù)學(xué)知識、技能解決現(xiàn)實情境問題的能力，將數(shù)學(xué)建模與數(shù)學(xué)素養(yǎng)緊密聯(lián)系，并將數(shù)學(xué)建模周期理論作為整個評價框架的基石。而且，其評估對象是接近完成或已經(jīng)完成義務(wù)教育的15周歲學(xué)生。所以，不管從測量內(nèi)容上，還是從測量對象上，PISA的數(shù)學(xué)素養(yǎng)評價理論對初中數(shù)學(xué)建模教學(xué)都具有重要的指導(dǎo)意義。

一、PISA數(shù)學(xué)素養(yǎng)評價框架下的數(shù)學(xué)建模周期理論

PISA2015數(shù)學(xué)素養(yǎng)評價框架如圖1所示。它包含了四種內(nèi)容、四種情境、七種技能和四個過程，而最里層中心位置描述的就是數(shù)學(xué)建模周期。從PISA2003到PISA2015，雖然數(shù)學(xué)素養(yǎng)的評價框架中數(shù)學(xué)素養(yǎng)和七種技能等一些核心概念的定義都經(jīng)過多次修改，但每一次都是以數(shù)學(xué)建模周期為基石，足見數(shù)學(xué)建模周期理論在PISA數(shù)學(xué)素養(yǎng)評價框架中的地位。

在PISA2003中，數(shù)學(xué)建模周期被稱為數(shù)學(xué)化周期，由PISA2003數(shù)學(xué)專家組主席de Lange提出。de Lange是著名數(shù)學(xué)教育家，其領(lǐng)導(dǎo)的荷蘭弗賴登塔爾數(shù)學(xué)教育研究所強調(diào)繼承和發(fā)展弗賴登塔爾的數(shù)學(xué)化思想，認(rèn)為將情境問題轉(zhuǎn)為數(shù)學(xué)問題求解是一種數(shù)學(xué)化的體現(xiàn)，所以將這個流程命名為數(shù)學(xué)化周期。但是，由于數(shù)學(xué)化的內(nèi)涵更為豐富，不僅包含與數(shù)學(xué)建模類似的從外部情境到數(shù)學(xué)內(nèi)部的水平數(shù)學(xué)化，還包含數(shù)學(xué)系統(tǒng)內(nèi)部的垂直數(shù)學(xué)化。所以，到PISA2012中，該流程改稱為數(shù)學(xué)建模周期。一直到PISA2015，都延續(xù)了此名稱。此名稱也就成了PISA的一個核心專業(yè)術(shù)語。

PISA的數(shù)學(xué)建模周期，雖然有不同的提法，但是基本上大同小異，描述了應(yīng)用數(shù)學(xué)解決現(xiàn)實情境問題的一個完整流程，包含了數(shù)學(xué)建模的多個不同階段：從現(xiàn)實情境問題出發(fā)，通過數(shù)學(xué)化地表達，將情境問題轉(zhuǎn)化為數(shù)學(xué)問題;然后，應(yīng)用數(shù)學(xué)概念、事實和推理解決數(shù)學(xué)問題;緊接著，將數(shù)學(xué)結(jié)果闡釋為情境結(jié)果;最后，應(yīng)用情境結(jié)果對情境問題進行評價。當(dāng)然，這只是一個數(shù)學(xué)建模周期，一個理想的簡化版本，并不是說學(xué)生經(jīng)歷了這個周期，就可以完全解決情境問題。學(xué)生有可能進行到某一個過程時，會發(fā)現(xiàn)不合理，需要開始新的建模周期。例如，學(xué)生已經(jīng)將情境問題轉(zhuǎn)化成某個數(shù)學(xué)問題，但是在求解的過程中，發(fā)現(xiàn)數(shù)學(xué)問題無法解答，于是又回到情境問題，重新假設(shè)和抽象，轉(zhuǎn)化成新的數(shù)學(xué)問題，開始新的數(shù)學(xué)建模周期。解決一個真實的情境問題可能需要數(shù)次迭代，經(jīng)歷多個數(shù)學(xué)建模周期。

二、PISA數(shù)學(xué)建模周期的三個過程

在數(shù)學(xué)建模活動中，鼓勵學(xué)生經(jīng)歷完整的數(shù)學(xué)建模周期，培養(yǎng)學(xué)生完整的數(shù)學(xué)建模能力，是數(shù)學(xué)建模教學(xué)的最終目標(biāo)。但是，PISA并不測量學(xué)生完整的數(shù)學(xué)建模能力。因為PISA是一個學(xué)生素養(yǎng)評估項目，需要學(xué)生在一定的時間內(nèi)完成多道測試題目。例如，PISA2012的數(shù)學(xué)素養(yǎng)正式測試卷就包含了72道題目。如果每道題目都需要學(xué)生經(jīng)歷完整的數(shù)學(xué)建模周期才能解決的話，題目的難度就會劇增，學(xué)生就幾乎不可能完成測試，也就達不到評估的目的了。所以，PISA數(shù)學(xué)專家組精心設(shè)計試題，使一道試題只考查一個過程——將涉及的其他過程都設(shè)計好，只預(yù)留一個過程給學(xué)生執(zhí)行。

PISA認(rèn)為，數(shù)學(xué)建模周期中的闡釋和評估階段對七個數(shù)學(xué)基本技能的要求較為相似，并且在正式測試條件下沒有額外的資源來評估情境結(jié)果，所以，將這兩個階段合成一個過程，簡稱闡釋。PISA2012數(shù)學(xué)素養(yǎng)評價框架就只包含三個過程：建模、應(yīng)用和闡釋。下文將詳細闡述每個過程的定義，并通過PISA樣題來解釋這三個過程。

（一）建模

建模（formulate）是數(shù)學(xué)化地表達情境的簡稱，即“用數(shù)學(xué)方法描述情境”。在這個過程中，主要考查學(xué)生如何識別和確定情境問題的數(shù)學(xué)要素，怎么將情境問題數(shù)學(xué)化，怎么應(yīng)用合適的數(shù)學(xué)結(jié)構(gòu)來表示情境問題。這個過程可能包含若干認(rèn)知活動：提取重要變量、識別情境問題中的數(shù)學(xué)結(jié)構(gòu)（規(guī)則、關(guān)系和公式等）、簡化問題、數(shù)學(xué)化問題、用不同的方法表示問題、利用數(shù)學(xué)語言表示問題等。

例如，PISA樣題“比薩問題”就主要考查學(xué)生在這個過程中的表現(xiàn)：

比薩店提供兩種相同厚度、不同尺寸的圓形比薩。小的直徑為30 cm，價格為30 Zeds;大的直徑為40 cm，價格為40 Zeds。

請問哪種比薩更劃算？說明你的理由。

這里，Zed是PISA虛構(gòu)的貨幣單位，主要是從公平的角度考慮，讓來自不同國家和地區(qū)的學(xué)生處于同一情境中。在這個問題中，學(xué)生需要建立一個數(shù)學(xué)模型來刻畫比薩的價值。當(dāng)學(xué)生明確比薩厚度相同而直徑不同時，就可以將問題平面化，只考慮價格與面積的關(guān)系即可。確定這兩個變量后，學(xué)生需要建立表示單位面積價格的關(guān)系式，但不需要對關(guān)系式進行操作，只需代入數(shù)值比較大小即可。所以，這個問題主要考查學(xué)生將情境問題數(shù)學(xué)化的能力，可以歸入建模過程子量表。這個子量表的試題數(shù)量約占總試題數(shù)量的25%。

（二）應(yīng)用

應(yīng)用（employ）是應(yīng)用數(shù)學(xué)概念、事實、步驟和推理的簡稱，即“運用數(shù)學(xué)概念、事實、程序和推理”。這個過程主要考查學(xué)生運用數(shù)學(xué)概念、事實、過程和推理來解決數(shù)學(xué)問題，從而得出數(shù)學(xué)結(jié)論的能力，比如算術(shù)計算、解方程、從數(shù)學(xué)假設(shè)中進行邏輯推導(dǎo)、符號化、從圖表中提取數(shù)學(xué)信息、在空間中表示和操縱形狀、分析數(shù)據(jù)等。

例如，PISA樣題“行走問題”就主要考查學(xué)生在這個過程中的表現(xiàn)：

圖2顯示的是一個人行走的腳印，步長p是指兩個相鄰腳印底部之間的距離。

公式n/p=140近似地描述了p與n的關(guān)系，其中n表示一個人每分鐘行走的步數(shù)，p表示一個人以米為單位的步長。

（1）已知Heiko每分鐘行走70步，如果這個公式可以刻畫Heiko的行走，那么Heiko的步長是多少？

（2）已知Bernard的步長p是0.8米，應(yīng)用這個公式計算Bernard的行走速度，分別以千米/分鐘、千米/小時為單位。

這個問題的數(shù)學(xué)模型就是公式n/p=140，并且在題干中給出了。學(xué)生需要利用這個公式進行代數(shù)運算，并進行適當(dāng)?shù)耐评恚瑥亩鉀Q問題。這是一個典型的應(yīng)用數(shù)學(xué)概念、事實、程序和推理解決問題的過程。所以，這個問題主要考查學(xué)生數(shù)學(xué)內(nèi)部的問題解決能力，應(yīng)該歸入應(yīng)用過程子量表。這個子量表的試題數(shù)量約占總試題數(shù)量的50%。

（三）闡釋

闡釋（interpret）是闡釋、應(yīng)用和評估數(shù)學(xué)結(jié)果的簡稱，即“數(shù)學(xué)結(jié)果的解釋、應(yīng)用與評價”。這個過程主要考查學(xué)生反思數(shù)學(xué)問題的解決方案、結(jié)果或結(jié)論，并在現(xiàn)實問題背景下解釋這些數(shù)學(xué)結(jié)果和結(jié)論的能力。在這個過程中，學(xué)生要將數(shù)學(xué)問題解決的結(jié)果轉(zhuǎn)換到情境問題中，并確定這種結(jié)果是否與情境問題相符，具有現(xiàn)實意義。

例如，PISA樣題“垃圾問題”就主要考查學(xué)生在這個過程中的表現(xiàn)：

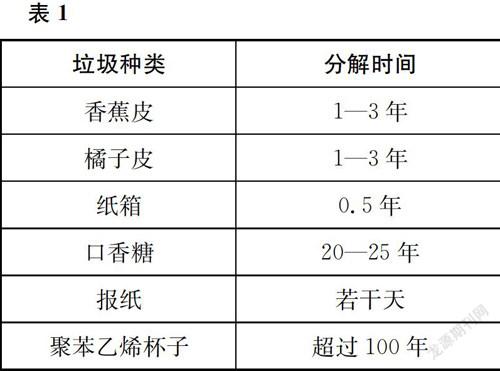
在一項關(guān)于環(huán)境的家庭作業(yè)中，學(xué)生們收集了人們丟棄的幾種垃圾分解時間的信息，如表1。

一個學(xué)生想用條形圖來顯示結(jié)果，請給出條形圖不適合顯示這些數(shù)據(jù)的一個原因。

在這個問題中，數(shù)學(xué)結(jié)果已經(jīng)給出，即一個條形圖，學(xué)生需要根據(jù)情境問題來評價用條形圖表示表格中數(shù)據(jù)的有效性，并給出理由。在情境問題中，已經(jīng)給出了幾種垃圾分解時間的數(shù)據(jù)，但是單位不同，學(xué)生需要從數(shù)學(xué)的角度思考數(shù)據(jù)與其表征之間的關(guān)系，并對表征的形式進行評估，提供條形圖不適合顯示所提供數(shù)據(jù)的原因。這個問題主要考查學(xué)生闡釋、應(yīng)用和評估數(shù)學(xué)結(jié)果的能力，應(yīng)該歸為闡釋過程子量表。這個子量表的試題數(shù)量約占總試題數(shù)量的25%。

三、數(shù)學(xué)建模教學(xué)的相關(guān)思考

上述建模、應(yīng)用和闡釋三個過程是數(shù)學(xué)建模周期的理論濃縮，為數(shù)學(xué)建模教學(xué)提供了很多啟示。

（一）關(guān)于數(shù)學(xué)建模能力的培養(yǎng)路徑

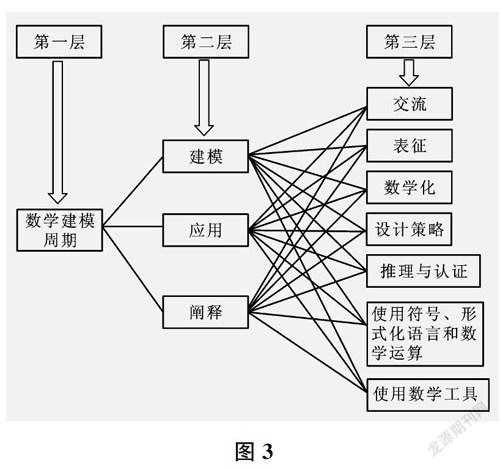
雖然數(shù)學(xué)建模活動涉及的大多是校外情境問題，但是，解決這些問題必須以學(xué)生校內(nèi)所學(xué)的數(shù)學(xué)知識、技能為基礎(chǔ)。如圖3所示，PISA認(rèn)為，學(xué)生在數(shù)學(xué)建模周期的三個過程中，都有可能用到七種數(shù)學(xué)基本技能。因此，學(xué)生數(shù)學(xué)建模能力的培養(yǎng)應(yīng)該從圖3中第三層的基本技能開始，再到經(jīng)歷單個的數(shù)學(xué)建模過程，最后經(jīng)歷完整的數(shù)學(xué)建模周期。這樣按部就班，循序漸進，幫助學(xué)生理解過程，體驗過程，最終完成過程。

由于數(shù)學(xué)基本技能培養(yǎng)涉及日常教學(xué)范疇，這里不做深入討論，但是其基礎(chǔ)地位應(yīng)該在數(shù)學(xué)建模教學(xué)過程中受到重視。特別值得一提的是數(shù)學(xué)工具的使用。數(shù)學(xué)工具包含物理工具（如直尺、量角器等）和電子設(shè)備（計算器、電腦等）。在信息化時代，使用信息技術(shù)解決數(shù)學(xué)問題的能力不僅是數(shù)學(xué)建模能力的基礎(chǔ)，更是大數(shù)據(jù)和人工智能等先進技術(shù)的基礎(chǔ)，培養(yǎng)學(xué)生這方面的能力在信息化時代尤為重要。

（二）關(guān)于數(shù)學(xué)建模任務(wù)的設(shè)計依據(jù)

《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版）》建議以課題研究的形式在高中開展數(shù)學(xué)建模活動，在某種程度上是對大學(xué)數(shù)學(xué)建模活動方式的一種效仿。但是無論《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011年版）》，還是已有的文獻研究，鮮有關(guān)于初中數(shù)學(xué)建模活動形式的探討。在初中學(xué)段，開展何種形式的數(shù)學(xué)建模活動是一個值得深入研究的課題。其中，最關(guān)鍵的問題是設(shè)計什么樣的數(shù)學(xué)建模任務(wù)去開展數(shù)學(xué)建模活動。

對此，PISA的數(shù)學(xué)素養(yǎng)測試問題給了我們一定的啟示。完整的、原汁原味的現(xiàn)實情境問題固然是好問題，但是，好問題也需要與活動對象、活動時間、活動環(huán)境相匹配。教師要因人制宜、因時制宜、因地制宜對真實情境問題進行深加工：不僅可以將問題細化到圖3中的單個過程，而且可以細化到圖3中的單個技能。將大問題微型化，使其可以方便快速地融入課堂教學(xué)，作為教學(xué)引入或課堂討論的內(nèi)容，從而在有限的時間里靈活地進行數(shù)學(xué)建模教學(xué)，在教師的引導(dǎo)下更加有效地幫助學(xué)生提高數(shù)學(xué)建模能力。

例如，對于數(shù)學(xué)建模活動“調(diào)查班級女同學(xué)擁有多少個布娃娃”，通過精心設(shè)計，可以產(chǎn)生不同的數(shù)學(xué)建模任務(wù)，聚焦不同的過程甚至技能。

聚焦“建模”過程的任務(wù)設(shè)計如下：

調(diào)查班上的八位女同學(xué)每個人擁有多少個布娃娃，請利用統(tǒng)計圖表表示調(diào)查結(jié)果。

這個任務(wù)需要學(xué)生建立數(shù)學(xué)模型表示調(diào)查結(jié)果。

聚焦“應(yīng)用”過程的任務(wù)設(shè)計如下：

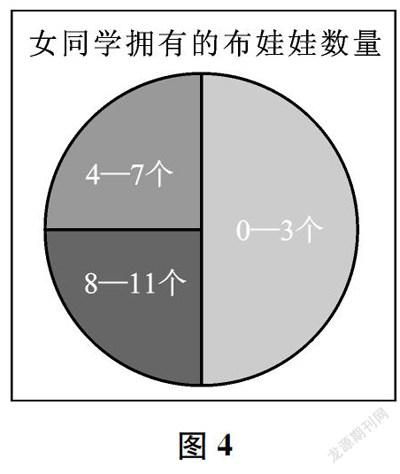
小明利用餅狀圖呈現(xiàn)了他的調(diào)查結(jié)果，如圖4所示。

根據(jù)小明制作的餅狀圖，以下哪一組數(shù)據(jù)符合小明的調(diào)查結(jié)果（）

A. 0，1，2，2，3，3，5，10

B. 0，1，2，3，5，6，9，11

C. 0，2，2，3，4，8，9，10

D. 1，1，1，1，4，4，8，8

E. 1，2，4，5，6，7，8，10

這個問題的數(shù)學(xué)模型（餅狀圖）已經(jīng)建立，學(xué)生需要應(yīng)用模型解決問題。

聚焦“推理與認(rèn)證”技能的任務(wù)設(shè)計如下：

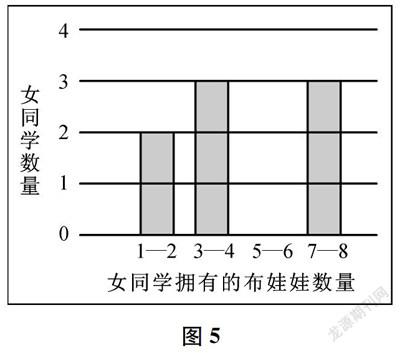
小芳利用條形圖呈現(xiàn)了她的調(diào)查結(jié)果，如圖5所示。根據(jù)小明與小芳的調(diào)查結(jié)果，列舉出八位女同學(xué)擁有的布娃娃數(shù)量，并說明理由。

這個問題需要利用統(tǒng)計推理與認(rèn)證能力解決。小明的調(diào)查結(jié)果表明：8人中4人有0—3個布娃娃，2人有4—7個，2人有8—11個。小芳的調(diào)查結(jié)果表明：8人中2人有1—2個布娃娃，3人有3—4個，3人有7—8個。綜合可知：8人中2人有1—2個布娃娃，2人有3個，1人有4個，1人有7個，2人有8個。

（三）關(guān)于數(shù)學(xué)建模能力的評價維度

怎樣評價學(xué)生的數(shù)學(xué)建模能力，特別是怎樣開展數(shù)學(xué)建模的形成性評價，以給教學(xué)提供更多的診斷信息，是在初中階段開展數(shù)學(xué)建模活動急需解決的問題。《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版）》建立了“情境與問題、知識與技能、思維與表達、交流與反思”四個維度的數(shù)學(xué)素養(yǎng)評價模型，并以此為依據(jù)建立了高中生的數(shù)學(xué)建模素養(yǎng)三層次水平評價模型。雖然不能完全將高中的評價框架移植到初中，但是可以借鑒由評價維度決定評價水平的思想。

數(shù)學(xué)建模周期的三個過程，不僅可以作為學(xué)生數(shù)學(xué)素養(yǎng)評價的三個維度，也可以作為學(xué)生數(shù)學(xué)建模能力評價的三個維度。通過評價學(xué)生如何有效地參與數(shù)學(xué)建模周期的每一個過程，可以給教學(xué)提供豐富的診斷信息。在建模維度中，評價學(xué)生如何抽象情境問題中的數(shù)學(xué)元素，聚焦學(xué)生將情境問題轉(zhuǎn)化為數(shù)學(xué)問題的能力。在應(yīng)用維度中，評價學(xué)生如何計算和操作，應(yīng)用所知道的概念和事實，尋找數(shù)學(xué)問題的解決方案，聚焦學(xué)生解決數(shù)學(xué)內(nèi)部問題的能力。在闡釋維度中，評價學(xué)生如何有效地反映數(shù)學(xué)解決方案或結(jié)論，并在現(xiàn)實問題背景下解釋它們，確定其是否合理，聚焦學(xué)生將數(shù)學(xué)結(jié)果解釋為情境結(jié)果的交流能力。

*本文系教育部人文社會科學(xué)研究規(guī)劃基金項目“中小學(xué)核心素養(yǎng)測評的模型建構(gòu)與實證研究”（編號：19YJA880012）和江西省高等學(xué)校教學(xué)改革研究課題“移動終端版數(shù)學(xué)軟件在高等數(shù)學(xué)教學(xué)中的應(yīng)用與實踐——以GeoGebra為例”（編號：JXJG-16-10-6）的階段性研究成果。

參考文獻：

[1] OECD（2013）.PISA 2012 Assessment and Analytical Framework：Mathematics， Reading， Science， Problem Solving and Financial Lite-racy.Paris：OECD Publishing[EB/OL].http：//dx.doi.org/10.1787/9789264190511-en.

[2] OECD（2013）.PISA 2015 Draft Mathematics Framework.Paris：OECD Publishing[EB/OL].http：//www.oecd.org/pisa/pisaproducts/Draft PISA 2015 Mathematics Framework.pdf.

[3] OECD（2004）.The PISA 2003 Assessment Framework：Mathematics， Reading， Science and Problem Solving Knowledge and Skills.Paris： OECD Publishing[EB/OL].http：//dx.doi.org/10.1787/9789264101739-en.