基于自適應遺傳算法Smith非線性PID的加熱爐溫度控制

張偉 李紹銘 閆成忍

摘要：由于工業加熱爐的溫度控制有很多不確定因素，導致系統呈現非線性并且加熱爐溫度控制有大滯后的缺點，很難做到對溫度的精確控制。本文引入自適應遺傳算法和Smith預估控制策略對加熱爐的溫度控制器進行改進，使得系統的調節時間縮短、滯后被抑制以及穩定性增強。實驗結果表明：該方法能夠有效地改進控制系統的超調、純滯后的缺點;明顯改善控制系統的動態性能和抗干擾能力，從而達到更好的控制效果。

關鍵詞：溫度控制;自適應;Smith控制器;抗干擾

中圖分類號：TP273?文獻標志碼：A?文章編號：1008-4657（2019）05-0013-05

0?引言

軋鋼加熱爐控制器的作用是軋制過程為鋼坯提供所需的溫度，并控制加熱爐內溫度的恒定。加熱爐溫度控制的好壞是衡量控制系統特性的重要依據之一[1]。然而，實際工業生產過程中由于加熱爐體積過大，內部溫度存在分布不均勻，檢測系統不能跟蹤實時溫度變化，導致無法建立精確的數學模型和有效的可控模型，并且工業生產中普遍采用的是PID控制算法，由于控制器的參數調整很麻煩，因而無法達到精確控制加熱爐內溫度[2]。針對加熱爐溫度控制的缺點。本文在傳統工業PID控制算法的基礎上，提出采用自適應遺傳算法、Smith預估控制和非線性PID控制相結合的方法[3]，充分利用各種算法的控制優點對增益參數的全局尋優和對滯后的預估補償。

1?非線性PID控制器模型

傳統的PID控制器數學模型[4]

非線性PID調節器中增益參數和反饋的控制誤差之間存在有函數關系。可以用函數關系式進行描述并在控制器的各個部分中發揮作用。所以控制能力比常規PID效果好。

2?控制器設計

2.1?自適應遺傳算法整定

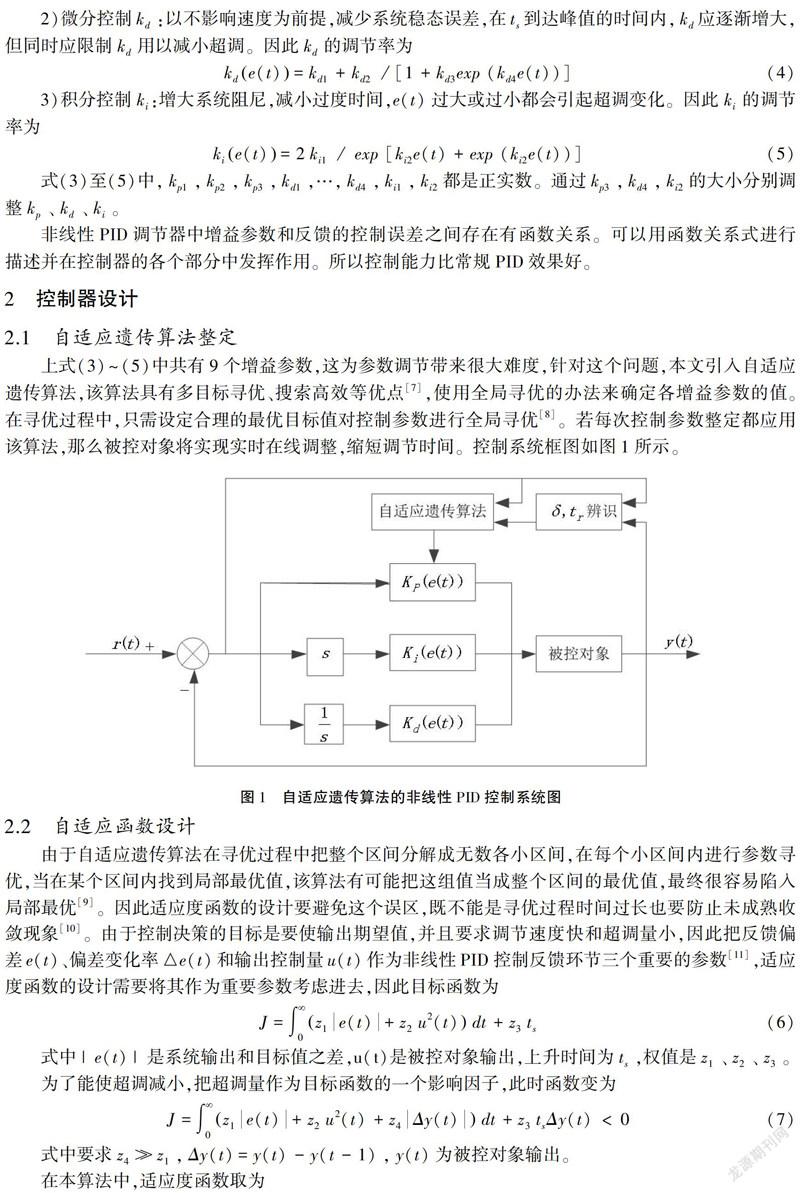
上式（3）～（5）中共有9個增益參數，這為參數調節帶來很大難度，針對這個問題，本文引入自適應遺傳算法，該算法具有多目標尋優、搜索高效等優點[7]，使用全局尋優的辦法來確定各增益參數的值。在尋優過程中，只需設定合理的最優目標值對控制參數進行全局尋優[8]。若每次控制參數整定都應用該算法，那么被控對象將實現實時在線調整，縮短調節時間。控制系統框圖如圖1所示。

2.2?自適應函數設計

由于自適應遺傳算法在尋優過程中把整個區間分解成無數各小區間，在每個小區間內進行參數尋優，當在某個區間內找到局部最優值，該算法有可能把這組值當成整個區間的最優值，最終很容易陷入局部最優[9]。因此適應度函數的設計要避免這個誤區，既不能是尋優過程時間過長也要防止未成熟收斂現象[10]。由于控制決策的目標是要使輸出期望值，并且要求調節速度快和超調量小，因此把反饋偏差e（t）、偏差變化率△e（t）和輸出控制量u（t）作為非線性PID控制反饋環節三個重要的參數[11]，適應度函數的設計需要將其作為重要參數考慮進去，因此目標函數為

自適應遺傳算法在非線性PID在增益參數確定和調整中有顯著的優越性，用遺傳算法對滯后問題的解決并沒有起到預期效果，需要在控制原理上進一步的改進。Smith預估控制在滯后問題上具有一定的補償能力，對系統的滯后補償有很好的效果并可以增強系統的穩定性。

2.3?Smith預估控制器原理

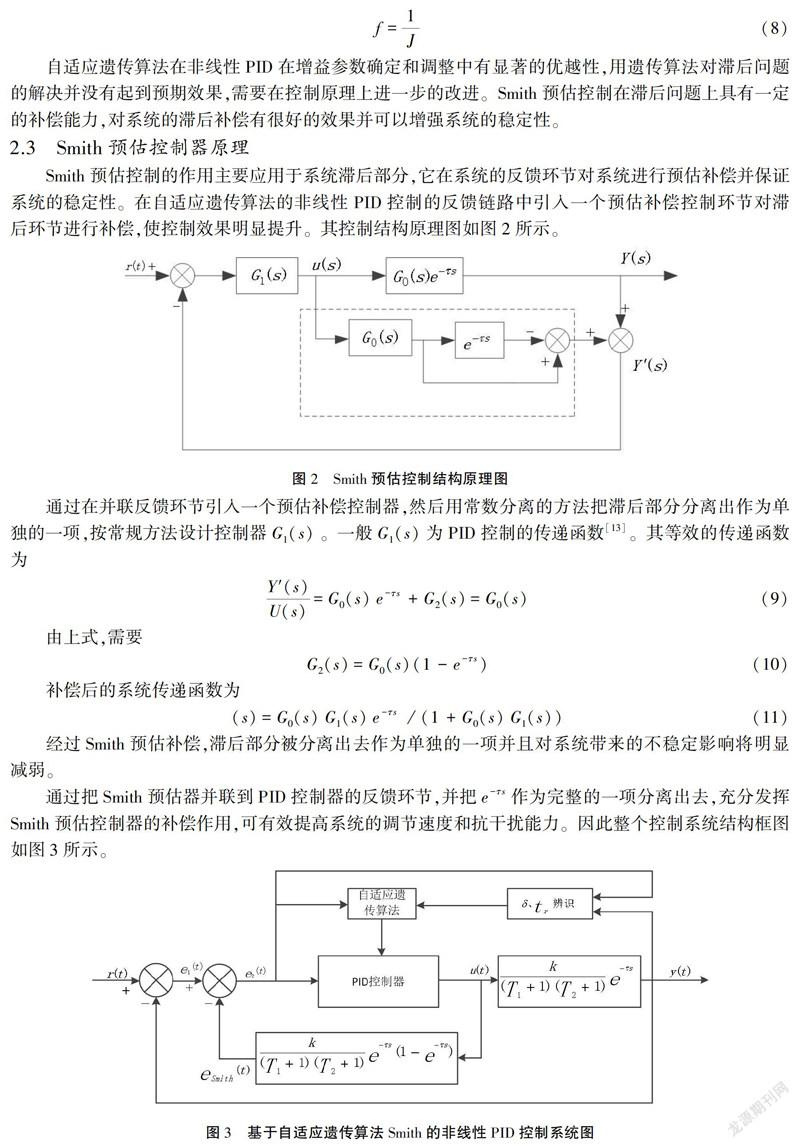
Smith預估控制的作用主要應用于系統滯后部分，它在系統的反饋環節對系統進行預估補償并保證系統的穩定性。在自適應遺傳算法的非線性PID控制的反饋鏈路中引入一個預估補償控制環節對滯后環節進行補償，使控制效果明顯提升。其控制結構原理圖如圖2所示。

通過在并聯反饋環節引入一個預估補償控制器，然后用常數分離的方法把滯后部分分離出作為單獨的一項，按常規方法設計控制器G1（s）。一般G1（s）為PID控制的傳遞函數[13]。其等效的傳遞函數為

經過Smith預估補償，滯后部分被分離出去作為單獨的一項并且對系統帶來的不穩定影響將明顯減弱。

通過把Smith預估器并聯到PID控制器的反饋環節，并把e-τs作為完整的一項分離出去，充分發揮Smith預估控制器的補償作用，可有效提高系統的調節速度和抗干擾能力。因此整個控制系統結構框圖如圖3所示。

在任意給定t采樣時刻，實際控制偏差是通過t時刻給定值r（t）和y（t）的差值得到

因此在非線性PID控制和自適應遺傳算法控制的基礎上，加入Smith預估控制可以對系統的滯后進行預估補償并且不影響系統對加熱爐溫度的控制。

3?自適應遺傳算法的Smith非線性PID控制在加熱爐溫度控制系統中的應用

產品質量的重要決定因素是加熱爐內部的加熱溫度，但加熱爐體積大、內部溫度分布不均勻，導致在生產控制過程中出現非線性、時變性、滯后性，控制難度大，對應的數學模型也是在理想條件下建立起來的。傳統的控制無法對爐內溫度達到精確控制[9]。針對此加熱爐建立數學模型，其傳遞函數為

式中，k的取值范圍為[0.2，0.8]，T1的范圍為[20，40]，T2的范圍為[20，40]，τ的范圍為[15，25]。對加熱爐溫度控制系統辨識，當k=0.5，T1=25，T2=35，τ=20時，隨機輸入（0，1）之間的任意數值，基于自適應遺傳算法的非線性Smith PID控制器采集樣本數為30，交叉概率和變異概率分別為：0.9、0.01;非線性PID控制器的參數kp1、kp2、kp3 的取值范圍為[0，5]，kd1、kd2、kd3、kd4 的取值范圍為[0，10]， ki1、ki2的取值范圍為[0，5]。最優指標 J 各項參數設置為 z1=0.999，z2=0.001，z3=2.0，z4=100，通過建立數學模型非線性PID控制器的各項參數如表1所示。

通過仿真實驗對本文的自適應遺傳算法的Smith非線性PID 控制算法進行評價，仿真過程模擬PID控制、非線性Smith PID控制和自適應遺傳算法的非線性Smith PID控制三種控制算法的控制速度、超調和穩定性并進行對比分析。仿真結果如圖4所示。

圖4是基于加熱爐溫度控制模型仿真的三條曲線分別為PID控制、Smith-PID控制和基于自適應遺傳算法的Smith非線性PID控制仿真結果，從圖中可以看出自適應遺傳算法的Smith非線性PID控制達到預設目標的速度比PID控制和Smith-PID控制要慢，這是因為非線性PID增益參數的確需要采用自適應遺傳算法的全局尋優方式，所需時間較長，而自適應遺傳算法的Smith非線性PID控制回到理想狀態的速度和超調量控制明顯優于其他兩種控制算法。

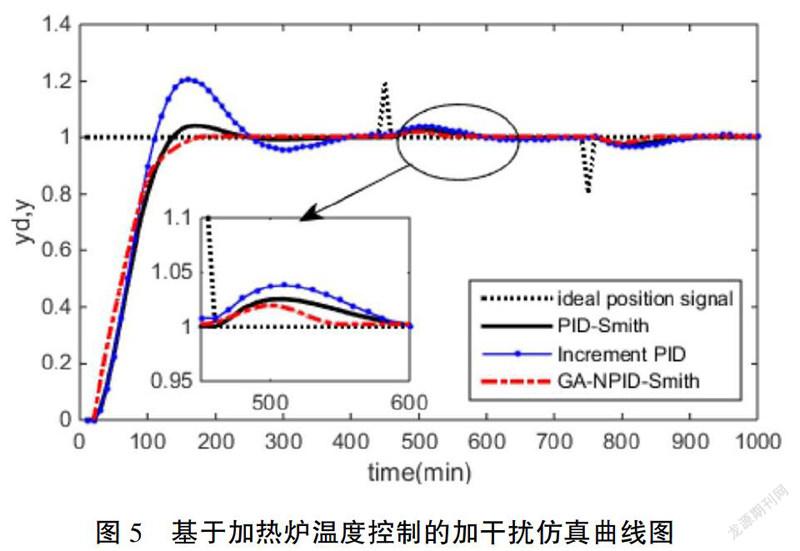
為了進一步驗證自適應遺傳算法的Smith非線性PID控制的穩定性和抗干擾能力，在三種控制方式下，隨機對其加上擾動，仿真結果如圖5所示。

由圖5中仿真結果可以看出，加入干擾后，自適應遺傳算法的Smith非線性PID控制的恢復能力要比其他兩種方式所需時間少。在抗干擾能力方面，本文中自適應遺傳算法的Smith 非線性PID控制有很好的抗干擾能力。

4?結論

本文將自適應遺傳算法的Smith 非線性 PID控制應用于加熱爐內溫度控制系統，非線性PID的增益參數通過自適應遺傳算法的全局尋優方式，找到最合適的增益參數，由Smith預估補償控制針對加熱爐溫度控制滯后的特點進行預估補償，最終使加熱爐溫度控制更加精確，在響應時間、超調量和振蕩方面都有明顯的改善，并且加熱爐對外界的干擾恢復能力明顯比其他兩種控制方式快。因此針對加熱爐溫度控制使用更加優化的參數尋優算法和軟件補償方法可以起到很好的控制效果，在無法快速提高硬件響應速度時，通過優化算法能夠使系統控制效果進一步提高。

參考文獻：

[1]解英杰，尤洋，謝慕君.Smith-Fuzzy-PID在集中供熱控制系統中的應用研究[J].計算機測量與控制，2014，22（9）：2 823-2 825.

[2]李陽.基于Smith-模糊PID的溫度跟蹤控制[D].武漢：華中科技大學，2017.

[3]高帥，楊少華，郭明安，等.基于遺傳算法自整定和Smith預估的電子倍增電荷耦合器件溫控系統設計[J].科學技術與工程，2016，16（29）：260-265.

[4]周穎，張磊，裘之亮，等.基于自適應遺傳算法的非線性PID控制器[J].河北工業大學學報，2010，39（1）：47-50，55.

[5]韓華，羅安，楊勇.一種基于遺傳算法的非線性PID控制器[J].控制與決策，2005（4）：448-450，454.

[6]程全，張凱.基于遺傳算法的溫度PID智能控制系統設計[J].沈陽工業大學學報，2018，40（4）：101-105.

[7]徐健義，楊遂軍，許啟躍，等.基于遺傳算法的半導體制冷器非線性PID設計[J].測控技術，2017，36（6）：51-55.

[8]干樹川，楊平先.基于模糊遺傳算法的PID自整定研究[J].華北電力大學學報，2005（5）：45-48..

[9]吳廷強，閻昌國，羅德蓮.基于積分分離模糊PID的溫度控制系統設計[J].西南大學學報（自然科學版），2017，39（5）：185-189.

[10]Bouyedda Hocine，Samir Ladaci，Moussa Sedraoui，et al.Identification and Control Design for a Class of Non-minimum Phase Dead-time Systems Based on Fractional-order Smith Predictor and Genetic Algorithm Technique[J].International Journal of Dynamics and Control，2019，7（03）：914-925.

[11]高錦，章家巖，馮旭剛，等.基于失配補償Smith-RBF神經網絡的主蒸汽壓力控制技術[J].重慶大學學報，2019，42（7）：105-113.

[12]Vidyadhar H Iyer，Mahesh S，Rohit Malpani，et al.Adaptive Range Genetic Algorithm：A hybrid Optimization Approach and Its Application in the Design and Economic Optimization of Shell-and-tube Heat Exchanger[J].Engineering Applications of Artificial Intelligence，2019，85：444-461.

[責任編輯：鄭筆耕]