“漢諾塔中的數學”教學設計

曾蓮秀

【摘要】漢諾塔是源于印度一個古老傳說的益智玩具。本課以漢諾塔器具為載體，以“探究-發現”為教學模式，通過引導探究操作最優策略的活動，培養學生觀察能力、倒推思維能力，以及有條理地闡述自己想法的能力，并初步體會遞歸思想。實現讓學生在實物操作中、在趣味游戲中開發思維潛能，提升思維水平的教學愿景。

【關鍵詞】漢諾塔 倒推 遞歸 思維訓練

益智器具：漢諾塔

教學目標：

（1）通過素材的搜集讓學生了解漢諾塔的起源、構造、游戲規則，并在游戲操作中正確、熟練移動4環以內的漢諾塔。

（2）通過操作漢諾塔并引導探究操作最優策略，培養學生觀察能力、倒推思維能力，初步體會遞歸思想，以及有條理地闡述自己想法的能力。

（3）通過游戲，培養學生積極向上的自信心和努力達到目的的意志力，并增強步步為營、深謀遠慮的意識。

教學過程：

師：科學家認為，人腦可以像肌肉一樣通過后天的訓練進行強化。通過思維訓練，能使我們的大腦變得越來越聰明。科學家還認為，益智游戲是培養兒童思維品質的重要途徑，你們喜歡玩益智游戲嗎？現在就讓我們隨著歡快的音樂，踏上智慧之旅吧。上課！

一、了解起源，明確規則

1.學生介紹游戲起源、構造

師：課前，老師布置你們去了解漢諾塔，說說看，關于漢諾塔你們都知道些什么？

生1：我知道漢諾塔源于印度一個古老傳說。傳說大梵天主創造世界的時候做了三根金剛石柱子，在一根柱子上從下往上按照大小順序摞著64片黃金圓環。大梵天主命令婆羅門將圓環不改變大小順序移到另一根柱子上。并且規定，在三根柱子之間一次只能移動一個圓環，大的圓環不能壓在小圓環上。法國數學家愛德華·盧卡斯根據這個傳說發明了現在的漢諾塔玩具。

生2：我知道漢諾塔由三部分組成：一個底座、三根柱子、一些圓環。

師：為了便于表述，咱們給這三根柱子取個名字，圓環所在的柱子叫起始柱，圓環要去的目的地柱子叫目標柱，另外一根起著過渡中轉的作用，我們稱它為過渡柱。

生：圓環按從上往下的順序，稱為第一環，第二環……

2.學生明確漢諾塔的游戲規則

教師演示錯誤的漢諾塔操作方法：一次性拿三個圓環，大的壓小的，讓學生辨析。

課件出示漢諾塔的游戲規則：一次只能移動一個圓環，大的不能壓在小的上面。

師：漢諾塔問題在數學界有著很高的研究價值，今天我們也當一回小小數學家，一起來研究漢諾塔中的數學問題。

二、實戰探索，引導探究

1.移動2個圓環

師：現在你們手中的漢諾塔有八層，試著移一移。（師巡視）

師：老師看到大家面有難色，我來采訪一下，你們都遇到什么困難？

生1：我在移動的過程中總會出現大的壓小的情況，就又撤回來了。

生2：移到后來，不知道怎么走了。

生3：移動這些圓環，感覺需要很多步數，感覺很難完成。

師：現在我們手中的漢諾塔有這么多層，如果沒有摸出一點門道就亂移一通，要不就走進死胡同，無法移動，要不來來回回走了很多冤枉路。鑒于這種情況，數學家的方法是，從簡單的問題入手，找到規律之后，再根據規律解決稍復雜的問題。好，咱們現在從兩個圓環起開始研究。

教師指名學生貼教具演示移動兩個圓環的過程，引發全班交流討論。

師：都是移動2個圓環，怎么這兩個同學移動的步數不一樣呢？

生：因為他們第一環移的位置不一樣，所以總步數就不一樣。

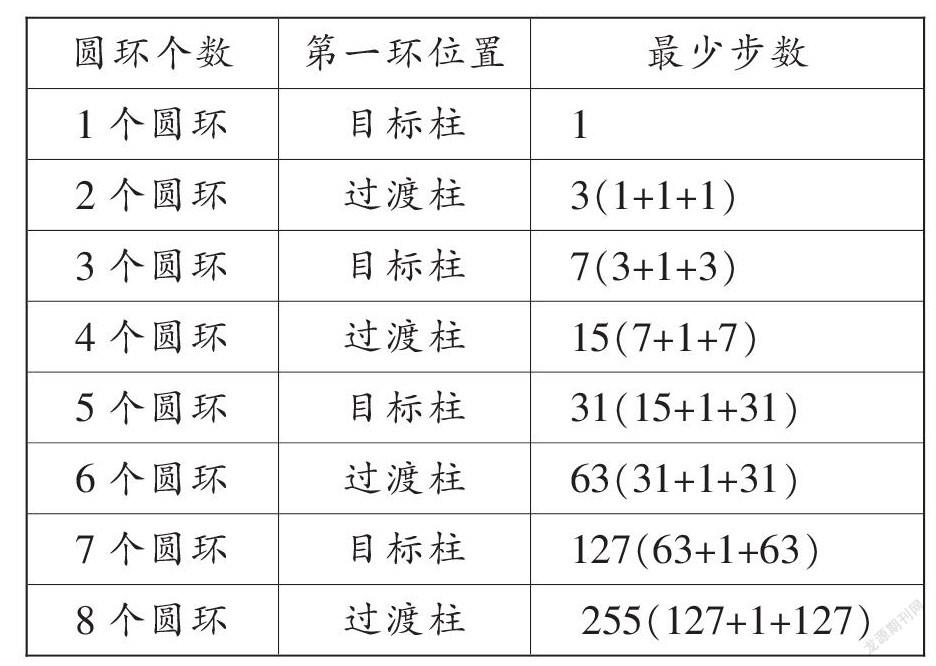
師：你觀察得真仔細！移動兩個圓環，有兩種移法：把第一環移到過渡柱，共需3步;把第一環移到目標柱，可能需要6步。3步與6步相比，顯然3步移法是最佳方案。看來，第一環的位置很重要啊，它能使我們的移動過程少走彎路。

教師組織學生填寫漢諾塔移動情況記錄單。

師：剛才我們經過嘗試、調整、優化，知道了移動兩個圓環最少需要3步。若不操作，你能推理說出用這3步的理由嗎？

生：下面的大圓環應該先到達目標柱，再把小圓環移到目標柱，這樣就不會出現大的壓在小的身上的情況。大圓環要先去目標柱，上面的小圓環就不能移到目標柱，所以第一環只能放在過渡柱上，等大圓環順利到達目標柱，再請小圓環回到大圓環上面，所以需要3步。

師：掌聲送給他，說得真好！這個同學先考慮底下的大圓環，再推想上面的圓環該去哪里合適，這種思考過程，在數學上稱為“倒推”。（板書：倒推）

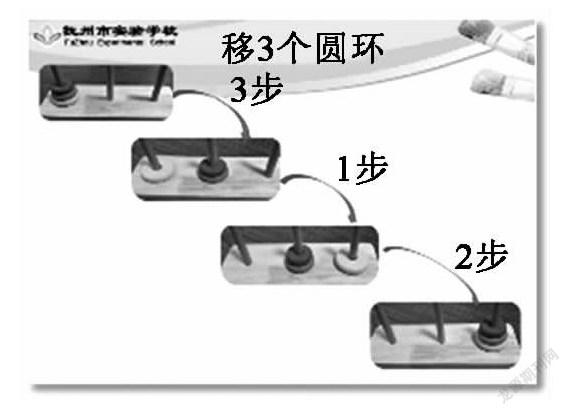
2.移動3個圓環

師：你能用這種“倒推”的想法，推想出3個圓環該怎么移動嗎？

說明要求：漢諾塔的起始柱放3個圓環，同桌先互相說說你是怎么推想的，再操作驗證，然后完成3個圓環操作記錄表。

指名學生貼教具演示移動三個圓環的過程，引導學生觀察交流。

師：觀察以上操作過程，你有什么發現？

生1：第一環放在目標柱上，步數最少，只需要7步。第一環放在過渡柱，步數更多，可能需要11步、14步。

生2：我發現，上面小圓盤和中圓盤從起始柱移到過渡柱上，至少要移3次，與剛才移動兩個圓環需要的步數是同樣的，要把它們從過渡柱移到目標柱的大圓環上面，也要3次，只是換柱子了。

生3：我發現移動3個圓環需要7步是這樣得來的：上面兩個圓環移到過渡柱，需要3步，再將一個圓環移到目標柱，需要1步，最后用同樣多的步數將兩個圓環移到目標柱，3+1+3=7步。

……

師：你們的思路如此清晰，老師真為你們感到驕傲！電腦博士也抑制不住激動的心情，用這三段動畫展示這三部分過程。

師：經過操作，同學們已經知道怎么移動3個圓環了，如果不操作，你能倒推說出這樣移動的理由嗎？

生：首先，要將最大環解放出來，移到目標柱，那么上面的兩個圓環就要移到過渡柱，上面兩個圓環要到過渡柱，那么第一個圓環就不能去過渡柱，所以第一個圓環應移到目標柱。

教師組織學生繼續填寫漢諾塔移動情況記錄單，并適時板書：最大■目標柱。

師：剛才同學們通過探究、交流，發現了3個圓環的最佳移動策略，還知道這么移的理由，真了不起！接下來是移3個圓環的練習時間，兩分鐘后，我們進行一次小競賽，速度快的同學可以獲得獎品。

3.移動4個圓環

師：現在我們一起回顧一下記錄單，共1個圓環，第一環放目標柱，共2個圓環，第一環放過渡柱，共3個圓環，第一環放目標柱，共4個圓環，第一環放哪里，步數才會最少呢？請你猜猜，再動手試試。

學生根據記錄單尋找移動規律，嘗試操作，匯報步數。

師：移動4個圓環最少需要多少步？誰能到黑板上用教具分幾段落講解？

生：移4個圓環最少用15步，整個移動過程可分三部分：將上面的三個圓環移到過渡柱用7步，再把最大的圓環移出來，移到目標柱用1步，最后又將3個圓環移到目標柱用7步。

師：分析得太到位了！前面探究獲得的結果以及研究方法可以幫助我們解決后面的問題，大家能舉一反三，觸類旁通，類推能力真強啊！

三、交流反饋，歸納規律

1.交流反饋，探究規律

師：剛才我們分別研究了1～4個圓環的移動方法和最少步數。你發現了什么？

生：……

師：移動圓環最少步數之間有沒有什么規律呢？

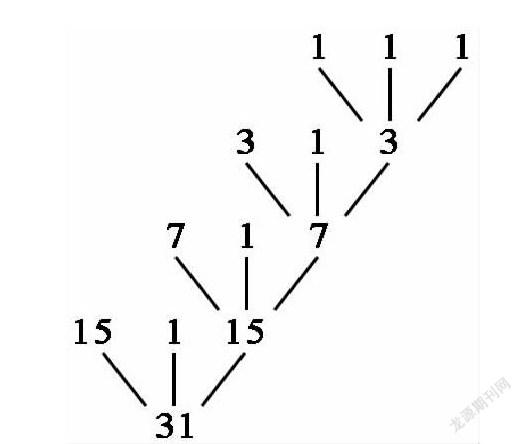
教師引導學生觀察由移動步數組成的數列：1，3，7，15……猜想和探究其中隱藏的規律。同桌討論交流，指名匯報。

師：根據你們發現的規律，請算一算，移5個圓環，最少需要多少步？

生……

師：5個圓環，最大環上面有幾個圓環？（4個）要想辦法將最大環之上的其他圓環移動到過渡柱上，于是就要“看5想4，看4想3，看3想2”。

教師適時板書樹狀遞歸分析圖。

師：像這樣，將復雜的問題不斷轉化成與之相似的較小問題，這種思想，在數學上稱為遞歸思想。（板書：遞歸）

2.運用思想，遷移延伸

師：請同學們應用遞歸思想計算出移動6個、7個、8個環最少需要的步數，并填寫完漢諾塔移動情況記錄單（如下表）。

四、評價激勵，升華提高

師：同學們，課后再去練習5層、6層、7層、8層環的移動。今天這節課就要結束了，你有哪些收獲和感受？快來說說吧。

生1：這節課，我認識了漢諾塔這款益智玩具，我會玩漢諾塔游戲了。

生2：我玩4層“漢諾塔”游戲遇到重重困難，終于挑戰成功，很開心。

生3：我知道動手操作時，要善于觀察和思考，不能盲目操作。

生4：我知道漢諾塔層數是單數時，第一環要移到目標柱，漢諾塔層數是雙數時，第一環要移到過渡柱上，這樣就不會走回頭路、走彎路，移動的步數就會是最少的。

生5：我知道每增加一個圓環，最少步數是上一次的2倍還要多1。

生6：我知道漢諾塔游戲中要用到倒推、遞歸的思想方法。

師：同學們的收獲真不少啊！一個小小的益智玩具里竟然蘊含著這么多的數學知識和數學思想。看來，只要大家用數學的眼光觀察，用數學的思維思考，就能在周邊的事物中發現更多的數學奧秘。下課！