基于能量過濾的不確定時間序列數據清洗方法

孫紀舟 李建中

摘 要： 精確度是數據科學領域研究的重要方面，對后續數據處理等過程都有至關重要的影響。利用多個傳感器返回的多個時間序列可提升時間序列數據的精確度，稱為不確定時間序列，這多個時間序列樣本在真實數據上下隨機波動。已有關于時間序列的研究大多直接在不確定時間序列上提出新算法，其缺點是算法復雜度通常較高，直接對不確定時間序列進行清洗，獲得盡可能接近真實的數據有重要意義。本文提出基于能量過濾的方法對不確定時間序列進行清洗，實驗結果表明與已有方法相比，本文方法在效果和效率上都更優。

關鍵詞： 不確定時間序列;能量過濾;數據清洗

文章編號：2095-2163（2019）04-0001-06 中圖分類號：TP391.41 文獻標志碼：A

0 引 言

時間序列數據在日常生活和工業生產中無處不在，例如氣象學中的溫度、濕度、風速、PM2.5;醫學中的心跳、血壓、體溫;以及經濟學中的股票指數、恩格爾系數以及其它描述宏觀經濟形勢的指數等。這些數據都是隨時間變化的數值型數據。由于環境干擾、傳感器的精度不夠、獲取數據時的舍入等原因，時間序列數據通常是不精確的，距離真實數據總有一些誤差。而這些誤差往往給人們的日常生活、醫療中的病情診斷及監控以及政府部門的決策等帶來負面影響。

為了盡可能降低誤差帶來的影響，常用的解決方法就是對同一時間序列數據采集多個樣本，每個樣本都在真實數據周圍隨機的上下波動，對這些樣本求平均值，或者直接在這些樣本上設計新算法，都能在一定程度上解決誤差帶來的影響。求平均值的方法最簡單快速，但結果精確度不夠高;設計新算法的思路能夠獲得更高的精度，但往往有著很高的時間復雜度。

結合時間序列平滑的特性以及隨機噪聲的波動特性，本文給出一種基于能量過濾的時間序列清洗算法。根據給定的時間序列樣本，計算出數據中噪聲所占能量的比重，根據這個比重找出一個頻率閾值，并將傅里葉變換之后高于該閾值的部分過濾掉，所得結果更加平滑且接近真實數據，在Top-k查詢問題上和已有算法做了實驗對比，結果顯示在效果上本文算法較好，而時間效率上本文算法遠遠優于已有算法。

1 問題描述

1.1 時間序列

1.2 不確定時間序列

在很多實際情況中，收集到的數據往往是不精確的，比如采集溫度數據的傳感器，本身有一定的誤差，為降低誤差，對同一時刻的數據收集多個數據樣本，以提高測量精度。 因此本文給出的不確定時間序列模型描述如下：

（1）不同時刻值的誤差是獨立同分布的隨機變量;

1.3 不確定時間序列的清洗

關于不確定時間序列的已有研究中，都致力于提出新的模型和算法對不確定時間序列數據進行搜索、聚類和Top-k查詢等。而相關問題在確定時間序列上的研究已經十分成熟，為了使這些方法能夠直接用在不確定時序數據上，本文主要研究如何對不確定數據進行清洗（或者還原），使之變為盡可能接近真實數據的確定時間序列。下面給出不確定時間序列的清洗問題。

2 基于能量過濾的清洗方法

由于數據點之間的相關性在頻域表現比較明顯，因此本文考慮在頻域進行降維，從而達到清洗數據的目的。其直觀思想是，時間序列數據在頻域上分布極不均勻。即有些頻率上的數據分布很集中（高能區域），而有些頻率上只有很少數據信息（低能區域），而不確定數據中的噪聲在各個頻率上的分布相對均勻。因此，在低能區域，噪聲數據占據主導地位，直接將其舍棄掉雖然會丟失一部分有用信息，但同時丟掉了更多的垃圾信息，使得整體的數據質量得到提升。 該方法的優點主要包括：

（1）大大減少了數據量，每個時間點的數據由m維降低到1維，并且在頻域上只需要保留很少的數據（例如在實驗中，長度為2 k的數據在頻率域只需要保留100個左右的數據點）;

（2）大大提升了數據質量，通過自適應的選取一個能量閾值，本文的方法能夠去掉盡可能多的噪聲，保留盡可能多的有用信息，從而使最終的估計結果盡可能地接近真實數據，實驗部分也對此進行了驗證。

2.1 離散傅里葉變換

即在某個頻率上，臟數據的能量的期望等于真實數據能量期望與噪聲能量期望之和。

2.3 噪聲能量的估計

由于不同時刻的數據都是由同一個傳感器收集的，因此不同時刻的隨機噪聲也是獨立同分布的。每個時刻有m個樣本，均由隨機變量s+Ns中采樣得到，其中s是真實值但未知，隨機變量Ns是傳感器的隨機誤差。由于s是常數不影響方差，因此s+Ns和Ns的方差相等，由概率論知識可知，m個樣本的樣本方差是對s+Ns方差的無偏估計，即是對Ns方差的無偏估計。 由于時間序列很長，因此在每個時間點上的數據估計Ns并求平均，根據大數定律容易得出，如此求得的方差幾乎等于傳感器隨機誤差的方差：

2.4 算法

至此，可給出基于能量過濾的時間序列清洗算法：

3 實驗驗證

最后在真實數據集和合成數據集上對本文算法和其它算法做一對比。

3.1 實驗環境

本文算法代碼用JAVA語言實現，硬件環境是主頻3.60GHz的8核Intel i7處理器，內存大小為8GB，硬盤大小1TB的臺式機，底層操作系統是Windows 7。

3.2 實驗數據

本實驗采用的數據集為UCR數據集，UCR是時間序列數據研究中最常用的數據集，樣本及噪聲的生成均采用文獻[1]中的方法。

3.3 算法對比

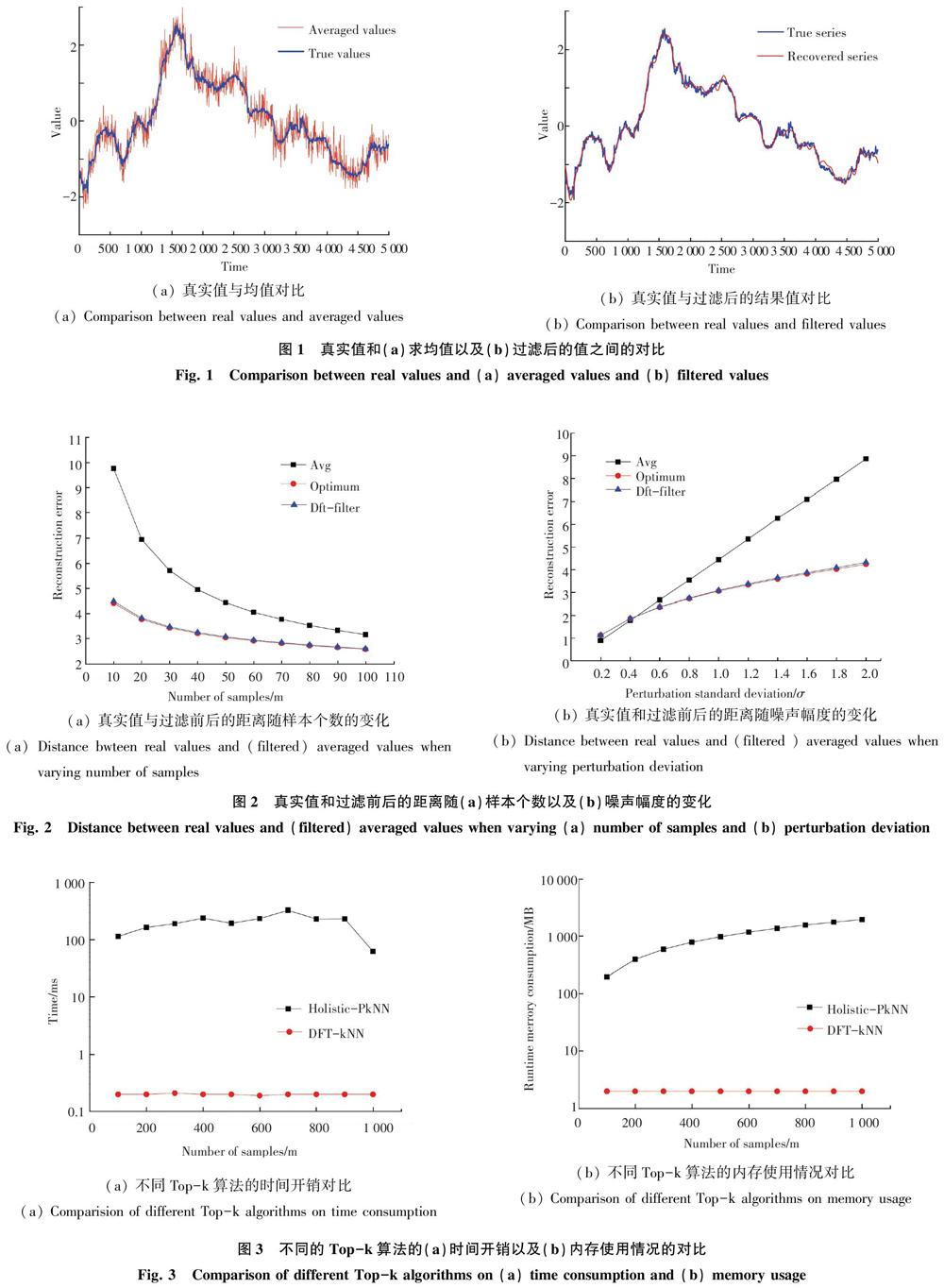
本實驗主要與一個最近的關于不確定時間序列數據上Top-k查詢的算法[1]Holistc-PkNN做對比。該算法解決的問題是，給定一個不確定時間序列數據集，研究如何從該數據集中快速找出與查詢序列Q距離最近的不確定時間序列。該方法是針對不確定時間序列上的老問題設計的新算法，其最大缺點是雖然設計了很多提高性能的優化技術，但時間開銷依然很高。