輪式機器人的末端位姿測量與誤差補償控制
陳曉生


摘 要:為了提高輪式機器人控制的穩定性,提出基于穩態跟蹤識別的輪式機器人的末端位姿測量與誤差補償控制方法,構建輪式機器人彈性連桿機構的動力學模型,在給定的加速度約束下進行輪式機器人彈性連桿機構的參數辨識,在機器人的運動平面內采用標準卡爾曼濾波模型進行運動姿態參數融合處理,根據輪式機器人的末端位姿進行參數自適應調節,采用比例-微分控制模型進行機器人的末端位姿測量與誤差補償控制,采用多步迭代方法實現輪式機器人的軌跡跟蹤和位姿測量,提高機器人的位姿精度。仿真結果表明,采用該方法進行輪式機器人的末端位姿測量的準確性較高,誤差補償控制能力較好,具有較好的穩健性和魯棒性。
關鍵詞:輪式機器人;末端位姿測量;誤差補償;控制
文章編號:2095-2163(2019)04-0274-04 中圖分類號:TP241.2?文獻標志碼:A
0 引 言
輪式機器人運行的穩定性是機器人設計的重要指標,為了確保輪式機器人的穩定性,需要對輪式機器人的彈性連桿機構進行優化設計,結合自適應控制律進行輪式機器人彈性連桿機構設計和位姿測量,提高位姿測量的精度,從而實現輪式機器人的運行空間規劃,建立輪式機器人彈性連桿機構的穩定性控制模型[1],采用步態跟蹤補償和空間姿態調節方法,進行輪式機器人彈性連桿機構的優化設計,降低輪式機器人彈性連桿機構的步態跟蹤誤差,構建輪式機器人彈性連桿機構參數優化辨識模型,實現末端位姿測量與誤差補償控制,研究輪式機器人的末端位姿測量與誤差補償控制方法,在機器人的優化控制設計中具有重要意義。對此,本文提出基于穩態跟蹤識別的輪式機器人的末端位姿測量與誤差補償控制方法,構建輪式機器人彈性連桿機構的動力學模型,在給定的加速度約束下進行輪式機器人彈性連桿機構的參數辨識,用比例-微分控制模型進行機器人的末端位姿測量與誤差補償控制[2],采用多步迭代方法實現輪式機器人的軌跡跟蹤和位姿測量,實現輪式機器人的末端位姿測量與誤差補償控制優化,最后進行實驗測試分析,得出有效性結論。
1 機器人彈性連桿機構動力學分析
1.1 機器人彈性連桿機構動力學模型
為了實現對輪式機器人末端位姿測量與誤差補償控制,首先用傳感器采集輪式機器人各機構的運動位姿、速度和人機交互信息,構建輪式機器人彈性連桿機構的動力學模型,輪式機器人彈性連桿機構動力學模型建立在數據采集和信息處理的基礎上,設機器人彈性連桿機構動力學特征采樣步長為η,機器人彈性連桿機構受到的阻尼力、位置力的影響下[3],得到彈性連桿機構動力學傳迭代函數為:
通過上述輪式機器人彈性連桿機構的參數識別結果,構建輪式機器人彈性連桿機構的動力學模型,在給定的加速度約束下進行輪式機器人彈性連桿機構的參數辨識[5]。
1.2 輪式機器人彈性連桿機構參數辨識
結合輪式機器人彈性連桿機構末端的位置誤差特點,在測量坐標系下,采用無跡卡爾曼濾波得到輪式機器人的連桿機構參數穩態周期解為:
根據輪式機器人彈性連桿機構的運動部件對應的質心求得穩定性運動慣量參數[6],實現彈性連桿機構空間規劃聯合協調控制,優化控制問題描述為:
令A∈Cn×n(n×n維復數空間),由此構建了輪式機器人彈性連桿機構的參數辨識模型,根據參數辨識結果進行自適應控制。
2 位姿測量與誤差補償控制優化
2.1 機器人彈性連桿機構的位姿測量
在構建輪式機器人彈性連桿機構的動力學模型的基礎上,提出基于穩態跟蹤識別的輪式機器人的末端位姿測量與誤差補償控制方法,在給定的加速度約束下進行輪式機器人彈性連桿機構的參數辨識[7],得到輪式機器人基座坐標系的旋轉特征量為:
根據機器人的末端位姿測量和信息融合結果進行機器人的誤差補償控制。
2.2 機器人的軌跡跟蹤的誤差補償控制
在輪式機器人彈性連桿機構的行為軌跡空間點的坐標系中,采用自適應參數調節方法,進行輪式機器人彈性連桿機構的線性空間規劃[9],得到輪式機器人彈性連桿機構軌跡跟隨糾偏的等價非線性時變反饋系數為:
采用比例-微分控制模型進行機器人的末端位姿測量與誤差補償控制,得到誤差補償融合的協方差矩陣為:
建立機器人彈性連桿機構與步態協調對應的狀態空間模型,采用跟蹤誤差和反饋調節方法得到控制律優化設計,采用比例-微分控制模型進行控制誤差補償和自適應參數調節[10],得到優化輸出為:
根據上述分析,用最小二乘法獲取未知數的解,形成實際輪式機器人彈性連桿機構空間D-H參數模型,實現輪式機器人的末端位姿測量與誤差補償控制。
3 仿真實驗與結果分析
為了測試本文方法在實現輪式機器人的末端位姿測量與誤差補償控制中的應用性能,進行仿真實驗分析,采用NDI 精密光學跟蹤設備進行機器人的位姿信息采集,步態規劃的跟蹤速度為 24 mm/s,慣性轉矩為 mr=1.13×104 kg,輪式機器人的空間標定半徑為R=2.05 m,根據上述仿真環境和參數設定,進行輪式機器人的末端位姿測量,得到位姿參數測量結果如圖1所示。
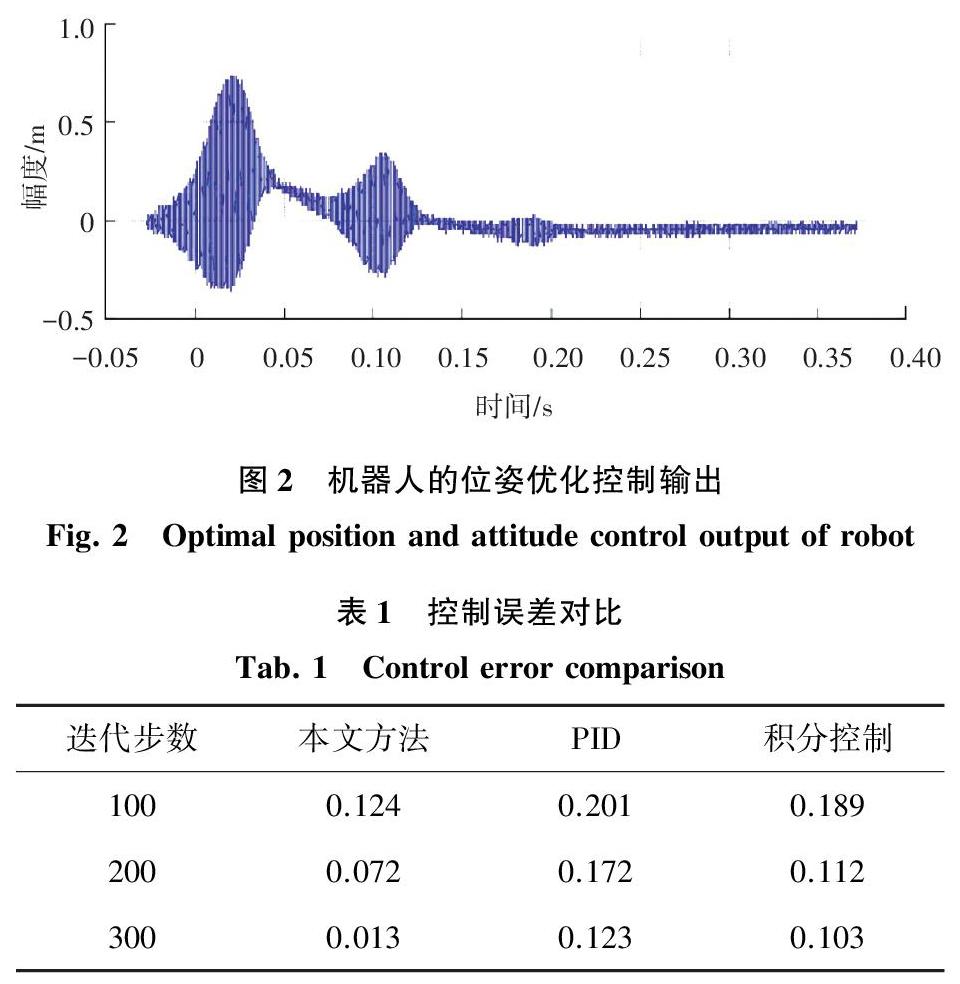
根據圖1的位姿參量結果,進行誤差補償控制,在給定的加速度約束下進行輪式機器人彈性連桿機構的參數辨識,在機器人的運動平面內采用標準卡爾曼濾波模型進行運動姿態參數融合處理,得到控制優化輸出如圖2所示。
分析圖2得知,采用本文方法進行機器人的末端位姿測量與誤差補償控制的輸出穩定性較好,收斂性較強,測試不同方法進行機器人的末端位姿測量與誤差補償控制的誤差,得到對比結果見表1,分析表1得知,本文方法進行機器人的末端位姿測量與誤差補償控制的精度較高,誤差較小。
4 結束語
對輪式機器人的彈性連桿機構進行優化設計,結合自適應控制律進行輪式機器人彈性連桿機構設計和位姿測量,提高位姿測量的精度,本文提出基于穩態跟蹤識別的輪式機器人的末端位姿測量與誤差補償控制方法,構建輪式機器人彈性連桿機構的動力學模型,在給定的加速度約束下進行輪式機器人彈性連桿機構的參數辨識,在機器人的運動平面內采用標準卡爾曼濾波模型進行運動姿態參數融合處理,根據輪式機器人的末端位姿進行參數自適應調節,采用比例-微分控制模型進行機器人的末端位姿測量與誤差補償控制,采用多步迭代方法實現輪式機器人的軌跡跟蹤和位姿測量。研究得知,本文方法進行機器人的末端位姿測量與誤差補償的精度較高,誤差較小。
參考文獻
[1]王碩,禹梅,譚文. 具有丟包補償網絡化控制系統的量化反饋穩定性分析[J]. 系統科學與數學, 2015, 35(3):287-297.
[2]景奉水, 楊超, 楊國棟, 等. 機器人軌跡糾偏控制方法研究[J]. 機器人, 2017, 39(3):292-297.
[3]王華,康榮杰,王興堅,等. 軟體彎曲驅動器設計與建模[J]. 北京航空航天大學學報,2017,43(5):1053-1060.
[4]王俊剛, 湯磊, 谷國迎, 等. 超冗余度機械臂跟隨末端軌跡運動算法及其性能分析[J]. 機械工程學報, 2018, 54(3):18-25.
[5]邸斌,周銳,董卓寧. 考慮信息成功傳遞概率的多無人機協同目標最優觀測與跟蹤[J]. 控制與決策, 2016, 31(4):616-622.
[6]Alzu'bi H, Mansour I, Rawashdeh O. Loon Copter:Implementation of a hybrid unmanned aquatic-aerial quadcopter with active buoyancy control[J]. Journal of Field Robotics, 2018, 35(5):764-778.
[7]趙延治,梁博文,邊輝,等. 全域恒平衡并聯機構構型設計與平衡特性分析[J]. 機械工程學報, 2019, 55(1):25-31.
[8]Ofodile N A, Turner M C. Anti-windup design for input-coupled double integrator systems with application to quadrotor UAV's[J]. European Journal of Control, 2017, 38:22-31.
[9]鐘大鑒,馮翔,虞慧群. 基于狀態轉移和模糊思考的遷徙優化算法[J]. 計算機科學,2019,46(1):112-116.
[10]周璠,鄭偉,汪增福. 基于多異類傳感器信息融合的微型多旋翼無人機實時運動估計[J]. 機器人,2015,37(1):94-101.

