基于Bezier曲線的低比轉速離心泵葉片包角優選

(長江大學機械工程學院，湖北 荊州 434023)

離心泵最重要的部件是葉輪，葉輪設計的優劣直接影響離心泵的性能，而葉輪設計中最重要的則是葉片的設計。葉輪的基本參數中葉片包角最為重要，葉片包角直接影響離心泵的揚程和效率[1]，因此，在葉輪設計中，合理選擇葉片包角顯得尤為重要。目前，對低比轉速離心泵葉片的進出口結構角、葉片數量、葉輪進出口直徑等參數，相關研究人員給出了較多的設計和優化方法[2～6]，但對低比轉速葉片包角優選問題涉及較少，而對低比轉速離心泵的研究則主要集中在性能仿真和參數優化設計：張興等[7]研究了葉片數對低比轉速離心泵性能影響，數值模擬了全流道三維非定常湍流，發現葉片數的變化對隔舌處的壓力脈動變化影響較大，隨著葉片數的增加，離心泵的揚程逐漸增大，當葉片數為5時，離心泵的效率最高；趙偉國等[8]基于流場仿真對比分析了葉片厚度對泵的外部特性及內部流場的影響，發現在一定范圍內，隨著葉片厚度的增大，泵的最優工況點向小流量偏移，最高效率略有提高，在額定工況下運行時的湍動能損失不斷增大；Chehhat A.等[9]通過CFD(計算流體動力學)仿真研究了葉片出口角對離心泵湍流流動和性能的影響，發現隨著葉片出口角的增大，水頭增大，水力效率提高，泵性能更好。為此，筆者以IS50-32-160型低比轉速離心泵為模型，通過Fluent軟件仿真預測不同葉片包角下泵的性能，旨在為低比轉速離心泵葉片包角的設計優選提供理論依據。

1 Bezier樣條曲線

離心泵繪型一般使用方格網保角變換法、扭曲三角形法或逐點計算法[10]，繪型較為麻煩且經驗占很大比重，而Bezier樣條曲線具有良好的形狀控制能力，采用Bezier樣條曲線繪制葉片型線能提高型線擬合的精度[11]。

一般地，稱方程：

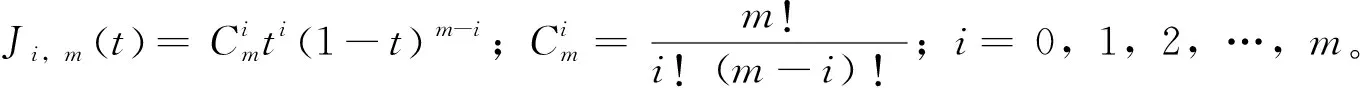
一般稱折線P0P1P2…Pm為曲線P(t)的控制多邊形，稱點P0,P1,P2,…,Pm為曲線的控制點。當參數t在區間[0,1]上變動時，就產生了Bezier樣條曲線。控制點的位置改變，Bezier樣條曲線形狀也隨之改變。工程中，經常使用三次或四次Bezier樣條曲線[13]。筆者使用五點四次Bezier樣條曲線，其方程展開式為：

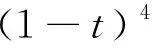
依次帶入點P0,P1,P2,P3,P4的坐標得到：

低比轉速離心泵(30～80)一般使用圓柱形葉片[14]，因此，z(t)=0。

2 葉片型線的繪制

圖1 葉片型線示意圖

如圖1所示，葉片包角為α，葉片進出口結構角分別為β1、β2，葉輪進出口半徑分別為r1、r2、P0、P1、P2、P3、P4是Bezier樣條曲線的5個控制點，L1、L3分別為P0P1與P4P3的延長線，兩者相交于點A，L2為出口圓的切線。圖中P0坐標為(r1,0)，P4坐標為(r2cosα,r2sinα)，P1、P3分別為線段P0A、AP4的中點。

由解析幾何關系可得到直線L1方程為：

y=cotβ1(x-r1)

直線L2方程為：

直線L3方程為：

y=-cot(α-β2)x+r2cosαcot(α-β2)+r2sinα

聯立直線L1與L3的方程，求解可得到A點的坐標：

由P1、P3分別為線段P0A、AP4的中點可得P1、P3的坐標，分別為：

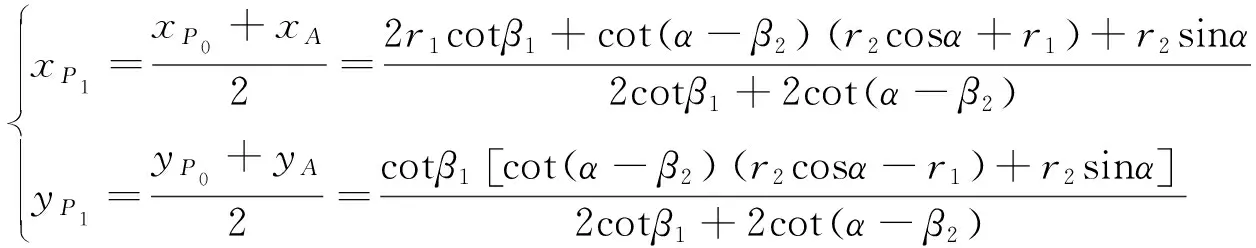
3 建模及求解設置

以IS50-32-160型低比轉速離心泵為研究對象，泵流量12.5m3/h，揚程32m，轉速2900r/min，比轉速46.36，泵吸入口直徑50mm，排出口直徑32mm，葉輪名義直徑160mm。根據相關文獻[15]，葉片出口結構角度在20～30°范圍內時性能最佳，低比轉速泵一般用8或9個葉片，取入口結構角和出口結構角分別為14.3°和22.1°，葉片數為8，包角則選取10、30、60、90、120、150、170°共7個計算型線方程，帶入上述基本參數計算A、P0、P1、P3、P4的坐標，根據得到的坐標再適當選取P2的坐標值。得到5個點的坐標后，帶入Bezier樣條曲線參數方程，得到曲線方程。將方程輸入到三維軟件中建立曲線，通過加厚等命令得到葉輪流道模型，再通過相應的繪型及建模得到蝸殼流道模型。入口液流速度要求均勻且垂直于進口界面，出口邊界條件要求出口液流充分發展，沿著流動方向無變化，因此在泵進出口均增加了一段擴散段，如圖2所示。

圖2 蝸殼流道模型 圖3 網格劃分

將繪制的流道模型導入ANSYS中，對進出口部分使用六面體網格劃分，其他部分使用四面體網格劃分，如圖3所示，將網格導入Fluent軟件中，設置葉輪區域為旋轉區域，轉速為5800π rad/min，入口為速度入口，出口為自由出口，工作介質為清水，選用標準k-ε湍流模型，求解采用simplec算法。取離心泵入口流量分別為5、10、15、20、25m3/h，監控模型出口壓力與出口速度。提取計算的數據后，分別計算揚程H(m)、軸功率N(kW)和效率η：

式中：p1、p2分別為進出口液體壓力，Pa；v1、v2分別為進出口液體速度，m/s；Z1、Z2分別為液體進出口相對高度，m；Mr為作用在葉輪上的力對轉軸的力矩，N·m；ρ為液體密度，kg/m3；g為重力加速度，9.8m/s2；n為轉速，rad/min；Q為入口流量，m3/h。

考慮到泵在實際使用中有容積損失與摩擦損失，按照文獻[10]給出的經驗公式，取容積效率與機械效率分別為0.95和0.86，對效率予以校正。

4 仿真結果與分析

4.1 外特性分析

圖4為仿真得到的不同葉片包角的離心泵性能曲線，隨葉片包角增加，揚程在額定流量附近有逐漸降低的趨勢，這是由于隨葉片包角增加，葉輪出口喉部面積減小，液體出口流道擴散降低，但隨著葉片包角增大，出口處喉部的平均安放角也減小，平均安放角減小對揚程造成的影響大于出口處喉部平均安放角減小對揚程造成的影響，最終導致揚程降低；額定流量附近所有葉片效率均為最高，由此可以看出最高效率點偏向于額定流量，泵效率隨葉片包角增加先緩慢增加后快速降低，當包角為120°時效率最高，泵性能最優。泵消耗功率隨流量增加逐漸增加，相同工況下，泵功率隨葉片包角增加而降低。

4.2 內特性分析

1)速度分布 圖5為通過仿真得到的額定流量附近葉片包角為10、30、60、90、120、150、170°時的跡線圖。從圖5可以看出，隨葉片包角增大，泵內部流道更加光順平整；當葉片包角小于120°時，葉輪流道很短，液體經過葉輪的水力損失小，但葉片包角小也導致流道擴散較大，葉片與液體間相對滑移較大；葉片包角小于120°時葉輪相鄰葉片間的流道出現了明顯的渦旋區，且包角越小渦旋區越大，這些渦旋區堵塞了流道，導致流道擴散程度降低，產生額外的水力損失，也增加了功率消耗，因此葉片包角較小時，葉輪功率很大但效率很低；而當葉片包角大于120°時，液體幾乎是沿著葉片工作面流動，相鄰葉片流道內的渦旋區基本消失，因此效率較高。但隨著葉片包角增大，流道也逐漸變長，過長的流道在對流體產生更強約束的同時也產生了較大的水力摩擦損失。因此，葉片包角在120°附近時效率最高。相同工況下，渦旋導致的額外功率消耗大于流道變長導致的額外功率消耗，功率隨葉片包角增加而逐漸降低。

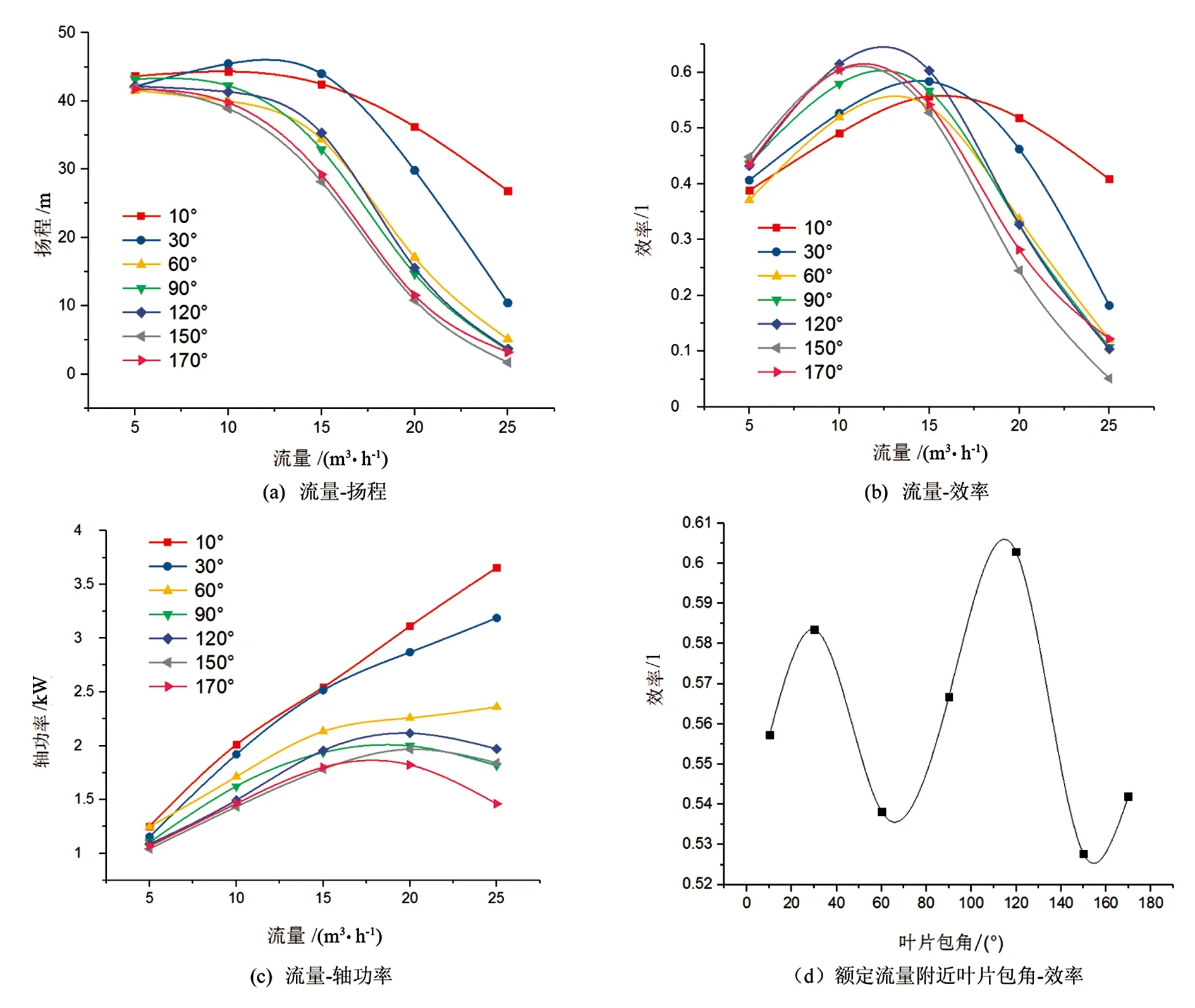
圖4 不同葉片包角的離心泵性能曲線

2)靜壓力分布 圖6為仿真得到的設計工況附近不同包角的靜壓力分布云圖。從圖6可以看出，葉輪內壓力并不是均勻分布的，主要是由于泵的蝸殼幾何結構不對稱，同時在葉輪旋轉時，蝸殼對葉輪有動靜干涉作用。液體從入口到出口，靜壓力逐步增加，隨流動所獲得的能量逐漸增加。在葉片包角低于120°時，云圖顯示在流道內低壓區面積較大，而在葉片包角大于120°時，葉片流道內低壓區面積減小。由此可以看出，當葉片包角較低時，容易產生空化現象。但在葉輪出口附近，高壓區出現了降低的趨勢，說明包角過大也產生了較大的水力損失，泵的揚程也因此降低。

3)湍動能分布 圖7為仿真得到的設計工況附近不同葉片包角時泵內部湍動能分布。從圖7可以看出，在蝸殼隔舌處的流道內，產生了較大的湍動能，且從隔舌處到蝸殼出口處的湍動能也較大，葉輪出口處湍動能也呈現出局部偏大的趨勢，說明液體在葉輪出口尤其是隔舌附近沖擊較大；在隔舌到泵出口段，湍動能隨葉片包角增加而逐漸降低，湍動能越大的位置越容易產生湍流渦。由此可以看出，葉片包角較小時，在蝸殼隔舌至出口處的流道內易產生湍流渦，導致泵效率降低；當葉片包角為60°時，葉輪內部有較大的湍動能。這也說明葉片包角較小導致對液體約束不夠，其內部產生了渦旋。

5 結論

1)Bezier樣條曲線具有良好的形狀控制能力，使用Bezier樣條曲線能方便地獲得除葉片包角外其他因素不變的模型，便于研究分析。

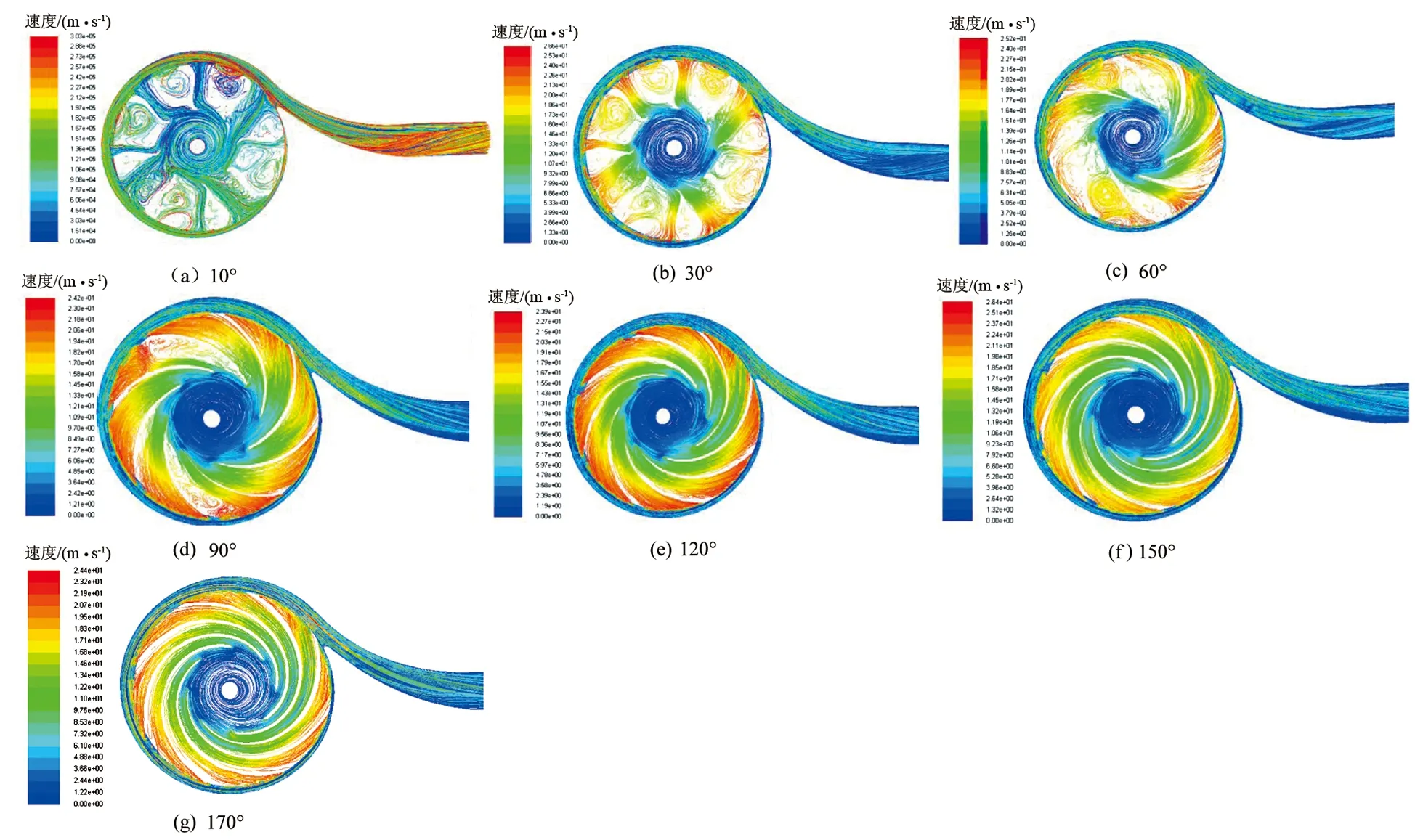
圖5 額定流量時不同葉片包角的跡線圖

圖6 額定流量時不同葉片包角的靜壓力分布云圖

2)仿真結果表明，標準k-ε湍流模型能較好地描述這種泵在額定工況點附近的流動規律，仿真計算結果分析能為這種低比轉速離心泵的性能優化提供有價值的信息，為進行基于CFD的離心泵設計和優化積累經驗。

圖7 額定流量時不同葉片包角的湍動能分布

3)通過CFD仿真得到葉片包角為120°時低比轉速離心泵性能最優，當葉片包角大于或小于120°時，低比轉速離心泵性能均有不同程度降低。