拉格朗日乘數法在多元函數求極值中的應用研究

劉美玲

（上海電機學院文理學院，上海201306）

條件極值是在某附加條件下的極值。 是數學分支最優化理論中被廣泛應用的概念，無論對于求解不等式，解析幾何問題，經濟學中求效益最大化，工程優化問題，進程管理，只要能將問題構造出優化模型，就能應用求條件極值的方法求解。 它是最優化理論中單目標規劃的核心數學問題，拉格朗日乘數法將條件極值問題轉化為無條件極值問題，是一種罰函數法。這種方法將一個目標函數和若干個約束條件，包括不等式約束條件，通過作輔助的拉格朗日函數轉化為無條件極值問題，其變量不受任何約束。這種方法引入了一個新的參數未知數，即拉格朗日乘數：約束條件所有方程的梯度（gradient）的線性組合里每個向量的系數。 微積分中為了簡單理解，一般是只有一兩個等式約束條件的極值問題，拉格朗日乘數是約束條件在輔助函數里的系數，也是駐點方程里約束梯度的系數。

1 定義介紹

求解二元函數z=f（x，y）在附加條件φ（x，y）=0，ψ（x，y）=0 下的極值點，先構造拉格朗日函數：

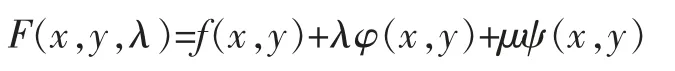
求解方程組：

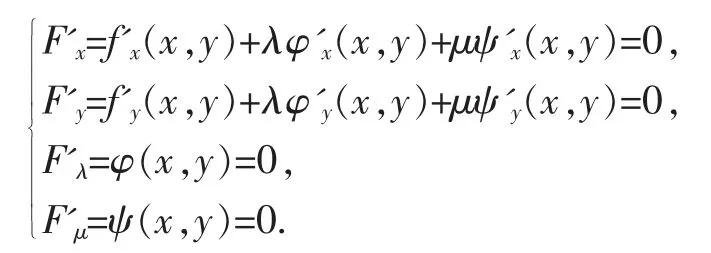
得到駐點（x，y），即可能的極值點。 若只有一個駐點，則由實際問題可直接確定此即所求的點。

2 幾何意義

為簡單計，這里只考慮二元函數且只有一個條件的情況。 如圖，所示，曲線為約束條件φ（x，y）=0，f（x，y）=C 為目標函數的等值線族。

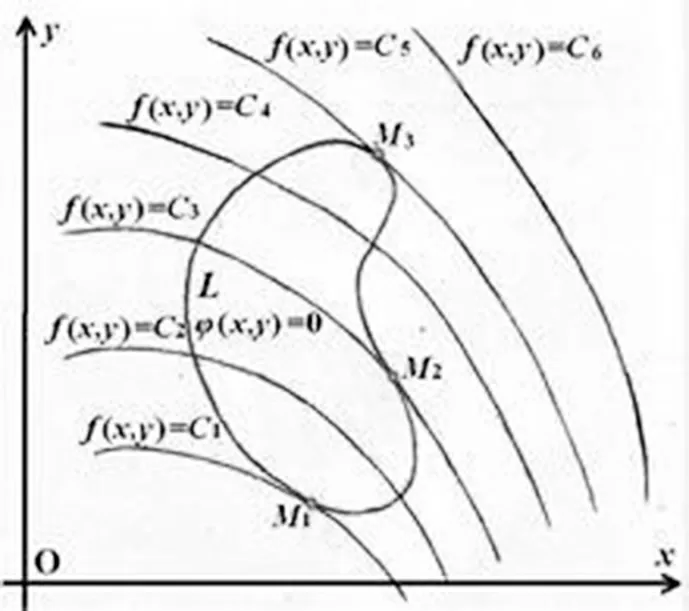
圖1 等值圖

在φ（x，y），f（x，y）的偏導數都連續的條件下，可能的極值點為M（x0，y0），從圖形上看，應是目標函數等值線族中與約束條件曲線能相切的那個切點。 因為兩曲線在切點處必有共同的法線，所以目標函數等值線在點M（x0，y0）的切平面法向量{f'x（x0，y0），f'y（x0，y0）}與約束條件曲線在點M（x0，y0）處的法向量{φ'x（x0，y0），φ'y（x0，y0）}平行，即：

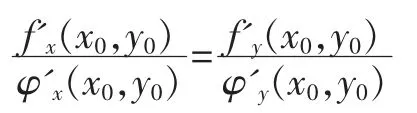
設這個比值為，得到：

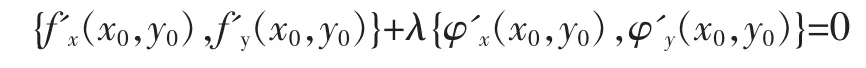
3 方法證明

設φ（x，y）=0 確定了隱函數y=ψ（x），則問題相當于求解z=f（x，ψ（x））的極值問題，故極值點必滿足：

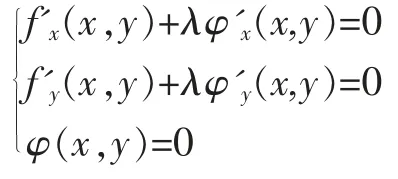
引入輔助函數F=f（x，y）+λφ（x，y），則極值點滿足：

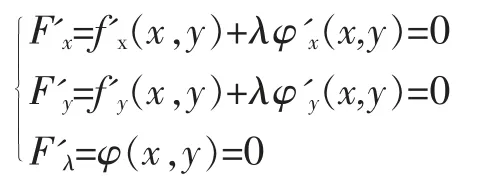
這里的F 就是拉格朗日函數，λ 稱為拉格朗日乘子，利用拉格朗日函數求極值的方法叫拉格朗日乘數法。

4 求極值舉例

例1：要設計一個容量為V0的長方體開口水箱，試問水箱長、寬、高等于多少時所用材料最省[2]？

解：設x，y，z 分別表示長，寬，高，則問題為求x，t，z，使在條件xyz=V0下水箱表面積S=2（xz+yz）+xy 最小。

令F=2（xz+yz）+xy+λ（xyz-V0），

解方程組：

本例計算也可以在公式xyz=V0中用x，y 表示出z，變成無條件極值求解。然而變量數較多的時候，則拉格朗日乘數法更簡潔易解。

例2：拋物面x2+y2=z 被平面x+y+z=1 截成一個橢圓。 求這個橢圓到坐標原點的最長與最短距離。

解：這個問題實質上就是要求函數

f（x，y，z）=x2+y2+z2

在條件x2+y2=z 和x+y+z=1 下的最大、最小值問題。應用拉格朗日乘數法，令

L（x，y，z，λ，μ）=x2+y2+z2+λ（x2+y2-z）+μ（x+y+z-1）

對L 求一階偏導數，并令它們都等于0，則有

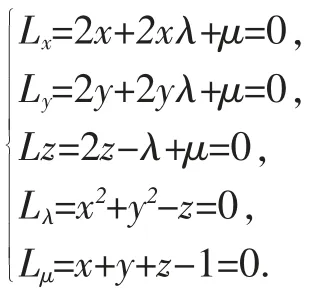
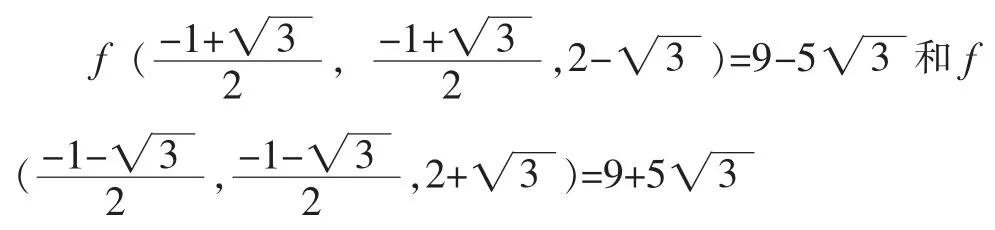
本例帶兩個約束條件，相對于例1，拉格朗日乘數法更為適用。因此通過簡單題目掌握了方法，從而可將其用到變量多，條件多甚至是帶不等式條件的問題上。

5 結論

作為一種優化算法，拉格朗日乘數法主要用于解決約束優化問題，即條件極值問題。通過引入拉格朗日乘子將含有一個n 元目標函數，k 個m 元約束條件的約束優化問題轉化為含有n+k 個變量的無約束極值問題。 無條件極值問題的求解相對簡單，有法可依，可通過求解駐點，再用梯度符號結合其他參數得到可行解。通過例題分析也不難發現，對于單目標多約束且存在偏導的問題，拉格朗日乘數法是一類非常好的方法，變量不多的情況下甚至可得到最優解。