針對圓形有界磁場中的運動戰略
黃昊曈
(江西省宜春市宜春中學高二15班 336000)
帶電粒子在勻強磁場中的運動作為物理最重要、最經典的模型,不僅能通過相關條件的改變進而構成情景多變的綜合題目,還能全面綜合考察學生的知識應用能力.除此以外,該物理模型還與生活、科技密切聯系,體現了物理與生活實際、科技與生產緊密結合的原則,如速度選擇器、質譜儀等.下面以粒子在圓形有界磁場中運動的典型題目為例,進行剖析.
一、駕馭運動軌跡與角度
例1如圖1,半徑為r=10 cm的勻強磁場區域邊界跟Y軸相切于坐標原點O,磁感強度B=0.332 T,方向垂直紙面向里.在O處有一放射源S,可向紙面各個方向射出速度為v=6.64×106m/s的α粒子.已知α粒子質量m=6.64×10-27kg,電量q=3.2×10-19C,試畫出α粒子通過磁場空間做圓周運動的圓心軌道,求出α粒子通過磁場空間的最大偏角.
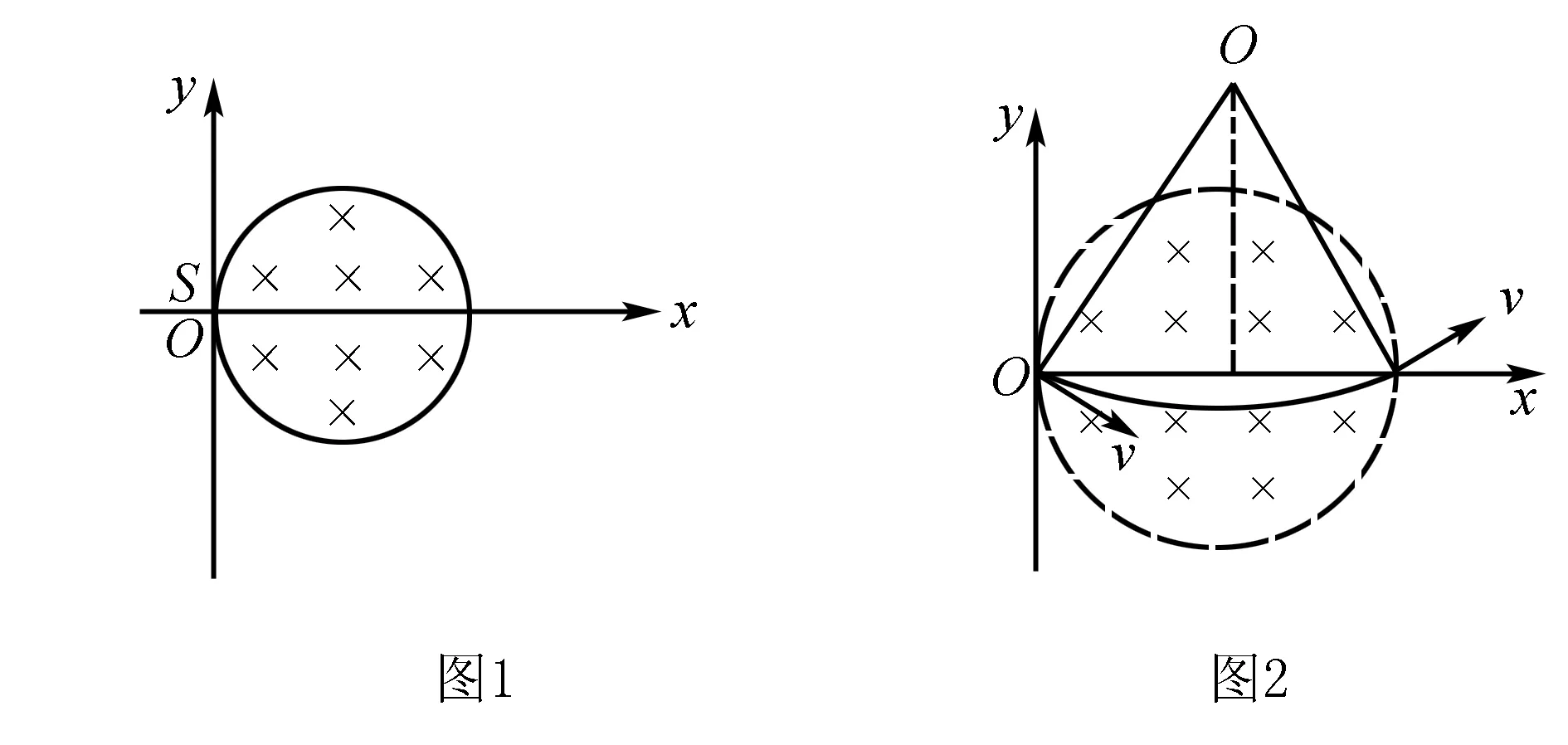
解析此題需要分析出只有從O點射入后此時的運動軌跡對應的弦最大,則離子通過磁場的偏角達到最大,進而得到最大弦是直徑.根據運動軌跡半徑公式有:R=mv/Bq代入數據得:R=0.2 m;經分析知要使得粒子在磁場空間的偏角最大,則圓的直徑為弦長,如右圖2,易知道圖中三角形為等邊三角形,則有:α=60°因此粒子在磁場中運動的速度的最大偏轉角也是60°.
反思此題是關于運動軌跡和角度問題,關鍵在于分析出圓的直徑是粒子運動軌跡所對應的最大的弦.此題可變形添加求解運動軌跡的面積一問,經過對例題的分析,已經知道軌跡半徑r=0.2 m,所以面積S=πr2=3.14×0.22=0.1256 m2.
二、把握運動速度和時間
例2一種速度選擇儀的模型如圖3所示,絕緣圓筒中勻強磁場的磁感應強度是B,方向沿軸線,半徑為R.質量為M,電量為Q的正粒子(忽略重力),分別以不同速度V從筒壁的A孔沿半徑方向進入筒內,假設粒子與筒壁的碰撞過程中無電量與能量的損失,使得粒子與筒壁連續碰撞,繞筒壁一周之后恰好又從A孔射出(其余粒子被吸收),問:
(1)能選出的粒子速度是多少?
(2)粒子能在筒中運動的時間是多長?
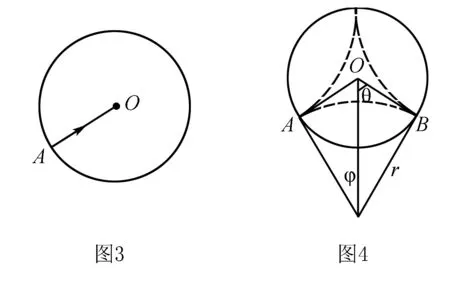
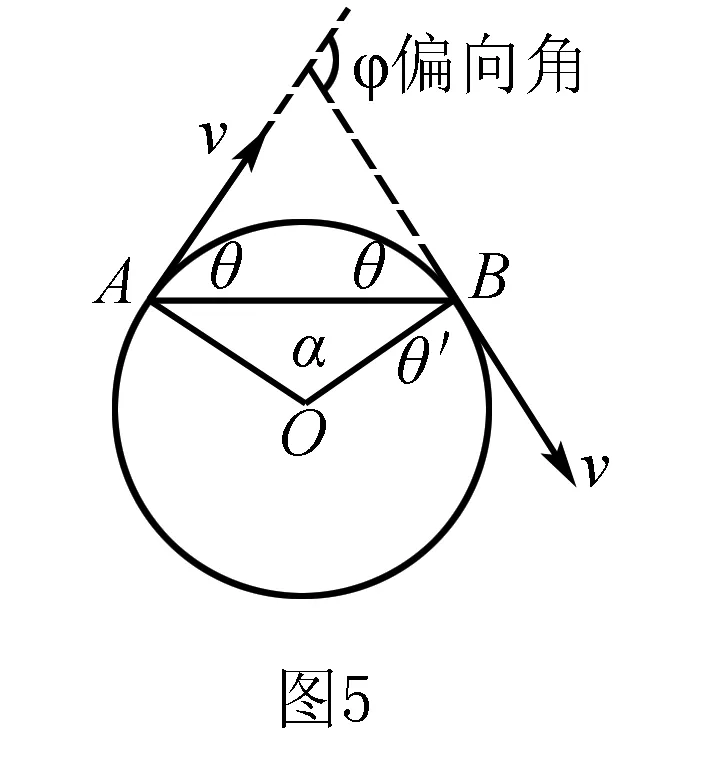
反思(1)利用洛侖磁力F確定圓心時需要憑借F⊥v畫出運動軌跡中任意兩點(通常取射入與射出磁場的這兩點)F的方向,并將其延長進而得到圓心的位置,由數學知識知道圓心也必在圓任意弦的中垂線上.
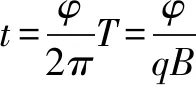
對于粒子在磁場中運動的考察方向是千變萬化的,既可以求解運動軌跡、半徑、速度、角度、時間,還可以求解運動軌跡的面積等.總之,圓心、半徑、時間構成了帶電粒子在圓形磁場中運動問題的三要素,其他眾多問題都是圍繞這三點進項展開的.因此把握三要素,認真審題,正確畫出運動軌跡,并結合數學知識,才能輕松解決此類問題.對于粒子在矩形、半圓形等勻強磁場運動的相關問題都可以以此為參照.

