基于Park模型對(duì)海上風(fēng)電場尾流的敏感性分析
陶英佳,黃小祥,周輝
基于Park模型對(duì)海上風(fēng)電場尾流的敏感性分析
陶英佳,黃小祥,周輝
(上海勘測設(shè)計(jì)研究院有限公司,上海 200062)
尾流的計(jì)算直接影響風(fēng)電場發(fā)電量的估算結(jié)果及項(xiàng)目財(cái)務(wù)指標(biāo),基于Park模型對(duì)某海上風(fēng)電場的尾流計(jì)算結(jié)果做敏感性分析,結(jié)果表明,尾流損失隨著值的變化呈現(xiàn)出二次函數(shù)的相關(guān)變化,隨著值的升高,尾流降低幅度越來越小;尾流損失隨著風(fēng)速的變化呈現(xiàn)出線性函數(shù)的相關(guān)變化,隨著風(fēng)速的提高,尾流也相應(yīng)地呈線性降低。
Park模型;尾流;海上風(fēng)電場;風(fēng)機(jī)
風(fēng)經(jīng)過風(fēng)力發(fā)電機(jī)后,由于葉輪吸收了部分風(fēng)能,風(fēng)力發(fā)電機(jī)的下游風(fēng)速出現(xiàn)一定程度的突變減小,而后又逐漸恢復(fù)。在風(fēng)電場中,多臺(tái)風(fēng)機(jī)間的尾流疊加又會(huì)影響其他受影響風(fēng)機(jī)的工作風(fēng)速,進(jìn)而影響其他風(fēng)機(jī)出力,導(dǎo)致全場的實(shí)際發(fā)電功率總是低于理論發(fā)電功率。
由于海面的粗糙度較小、湍流強(qiáng)度低,風(fēng)電機(jī)組尾流的影響距離較遠(yuǎn)。此外,海上風(fēng)電場工程裝機(jī)容量較大,多臺(tái)風(fēng)機(jī)間的尾流疊加影響較大,因此,陸上風(fēng)電經(jīng)驗(yàn)得到的尾流模型應(yīng)用在海上風(fēng)電場時(shí),往往會(huì)低估尾流的影響[1]。尾流的計(jì)算直接影響風(fēng)電場發(fā)電量的估算結(jié)果及項(xiàng)目財(cái)務(wù)指標(biāo),并影響項(xiàng)目前期投資方對(duì)項(xiàng)目的投資決策。綜上,在海上風(fēng)電項(xiàng)目設(shè)計(jì)過程中,對(duì)風(fēng)電場尾流的研究顯得尤為重要。本文基于Park模型對(duì)某海上風(fēng)電場的尾流計(jì)算結(jié)果做敏感性分析。
1 Park模型
描述風(fēng)電場風(fēng)機(jī)尾流的數(shù)學(xué)模型有多種,比如一維線性尾流模型、二維軸對(duì)稱渦粘模型、三維流體計(jì)算軟件仿真模型等。其中,最經(jīng)典且最常在工程項(xiàng)目中使用的兩類尾流數(shù)學(xué)模型分別是Park模型(一維線性模型)和Eddy模型(二維軸對(duì)稱渦粘模型)[2]。Park模型模型由丹麥Riso可再生能源實(shí)驗(yàn)室的Katic等人提出,目前已被廣泛應(yīng)用于風(fēng)能行業(yè)的風(fēng)能資源評(píng)估及發(fā)電量測算軟件中,該模型基于完成解析的數(shù)學(xué)表達(dá)式,擁有計(jì)算量低、響應(yīng)速度快、參數(shù)調(diào)整靈活等特點(diǎn)。
Park尾流模型的原理為:假定氣流經(jīng)過風(fēng)機(jī)葉輪后所形成的尾流沿風(fēng)機(jī)中心線呈軸對(duì)稱形態(tài),并且尾流寬度隨著下風(fēng)方向距離的增加而呈線性增加,但速度衰減逐漸恢復(fù)。
如果一臺(tái)風(fēng)力發(fā)電機(jī)的葉輪部分位于另一臺(tái)風(fēng)力發(fā)電機(jī)的尾流區(qū)域中,風(fēng)速衰減是與兩臺(tái)風(fēng)力發(fā)電機(jī)的葉輪重疊面積成比例:
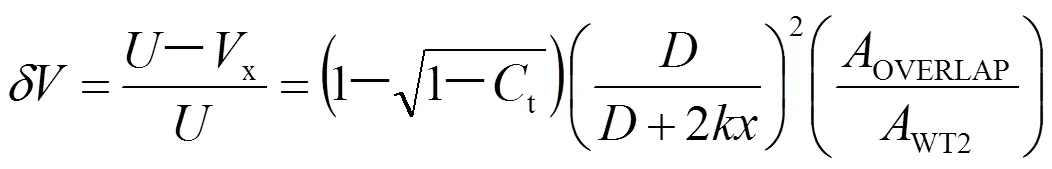
式(1)中:t為風(fēng)機(jī)推力系數(shù);為風(fēng)機(jī)直徑;OVERLAP為葉輪重疊面積;WT2為下游風(fēng)機(jī)葉輪面積。
2 風(fēng)電場概況
風(fēng)電場離岸距離約20 km,水深在20 m以上,場址面積約80 km2,擬規(guī)劃采用73臺(tái)單機(jī)容量為5.5 MW的風(fēng)力發(fā)電機(jī)組,風(fēng)電機(jī)組布置呈三角形形狀,一共布置五排風(fēng)力發(fā)電機(jī)組,風(fēng)電場布置及各個(gè)風(fēng)機(jī)編號(hào)如圖1所示。采用5.5 MW風(fēng)機(jī)標(biāo)準(zhǔn)空氣密度下的功率曲線和推力系數(shù)t值,作為計(jì)算輸入。根據(jù)上述輸入條件,值取0.05的情況下,本風(fēng)電場平均尾流損失為10.07%,由于后排受前排尾流疊加的影響,57號(hào)機(jī)位單機(jī)尾流最大,最大單機(jī)尾流損失達(dá)到了14.71%。

圖1 風(fēng)電場場址示意圖
3 尾流敏感性分析
在風(fēng)電場所選用機(jī)型和機(jī)型布置明確的情況下,采用Park模型計(jì)算得到的風(fēng)電場尾流主要取決于風(fēng)電場風(fēng)資源評(píng)價(jià)結(jié)論和模型中參數(shù)的選取。Park模型的核心在于通過定義尾流衰減因子來表示尾流的線性擴(kuò)張。尾流衰減因子與環(huán)境湍流及地面粗糙度相關(guān)。通常隨著環(huán)境湍流強(qiáng)度的增加而增大,常用取值為0.03~0.08。的取值不同會(huì)直接影響尾流損失與全場發(fā)電量計(jì)算結(jié)果。
風(fēng)電場風(fēng)資源評(píng)價(jià)結(jié)論需根據(jù)代表氣象站多年資料進(jìn)行長年訂正后得到,因此根據(jù)測風(fēng)塔數(shù)據(jù)直接進(jìn)行發(fā)電量計(jì)算存在一定不確定性。
綜上,本文主要從風(fēng)速和值兩個(gè)方面對(duì)風(fēng)電場的尾流進(jìn)行敏感性分析。在值取0.05的情況下,通過將各個(gè)扇區(qū)的風(fēng)速均提高2%~10%對(duì)尾流計(jì)算結(jié)果進(jìn)行敏感性分析;在風(fēng)資源成果不變的情況下,通過調(diào)整值對(duì)尾流計(jì)算結(jié)果進(jìn)行敏感性分析,調(diào)整區(qū)間為0.03~0.08。
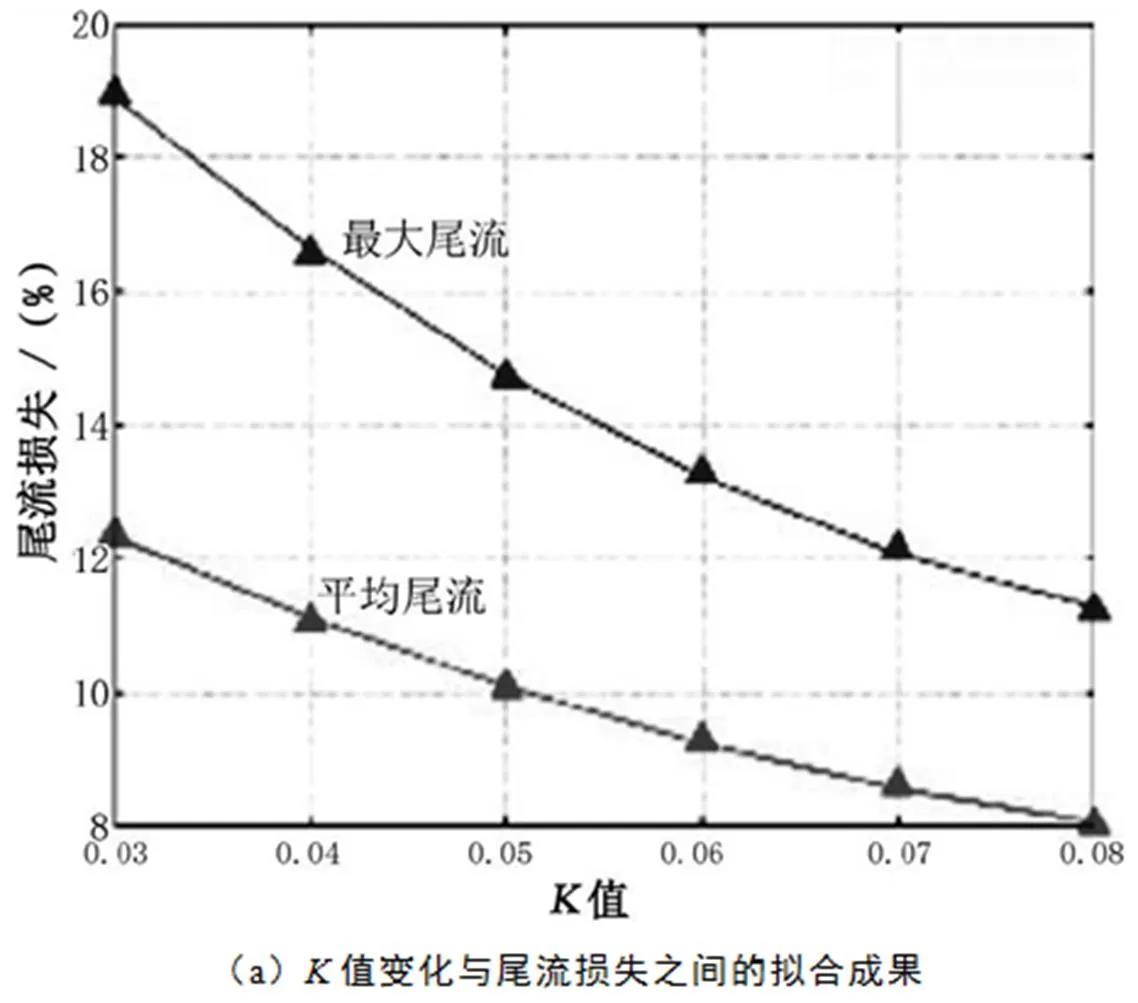
尾流計(jì)算結(jié)果如表1所示,值變化與尾流損失之間的擬合成果如圖2(a),風(fēng)速提高比例變化與尾流損失之間的擬合成果如圖2(b)。根據(jù)圖表結(jié)果可以發(fā)現(xiàn),在風(fēng)速一定的情況下,平均尾流損失和最大單機(jī)尾流損失隨著值的變化呈現(xiàn)出二次函數(shù)的相關(guān)變化,隨著值的升高,尾流降低幅度越來越小;在值一定的情況下,平均尾流損失和最大單機(jī)尾流損失隨著風(fēng)速的變化呈現(xiàn)出線性函數(shù)的相關(guān)變化,隨著風(fēng)速的提高,尾流也相應(yīng)地呈線性降低。
表1 尾流損失隨值、風(fēng)速變化表
K值平均尾流/(%)最大尾流/(%)風(fēng)速提高比例/(%)平均尾流/(%)最大尾流/(%) 0.0312.3618.94010.0714.7 0.0411.0716.5629.8014.2 0.0510.0714.7149.5213.7 0.069.2713.2669.2413.2 0.078.6112.1488.9612.7 0.088.0311.23108.6612.2
4 結(jié)語
本文介紹了Park模型計(jì)算尾流的原理,并簡單介紹了試驗(yàn)風(fēng)電場,通過對(duì)風(fēng)電場尾流的計(jì)算進(jìn)行敏感性分析,結(jié)果表明,在風(fēng)速一定的情況下,平均尾流損失和最大單機(jī)尾流損失隨著值的變化呈現(xiàn)出二次函數(shù)的相關(guān)變化,隨著值的升高,尾流降低幅度越來越小;在值一定的情況下,平均尾流損失和最大單機(jī)尾流損失隨著風(fēng)速的變化呈現(xiàn)出線性函數(shù)的相關(guān)變化,隨著風(fēng)速的提高,尾流也相應(yīng)地呈線性降低。
[1]程海鋒,胡志堅(jiān).海上風(fēng)電場風(fēng)電機(jī)組的尾流控制[J].水利規(guī)劃與設(shè)計(jì),2013(12):94-97.
[2]鄭愛玲,梁中榮.大型海上風(fēng)電場尾流損失計(jì)算方法對(duì)比[J].風(fēng)能,2016(1):84-86.
TM614
A
10.15913/j.cnki.kjycx.2019.17.015
2095-6835(2019)17-0036-02
〔編輯:張思楠〕

