帶有多項(xiàng)式約束的廣義分式規(guī)劃問(wèn)題的迭代算法

申培萍,班鳳麗

(河南師范大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院,河南新鄉(xiāng)453007)

1 引言

考慮如下一類帶有多項(xiàng)式約束的廣義分式規(guī)劃問(wèn)題

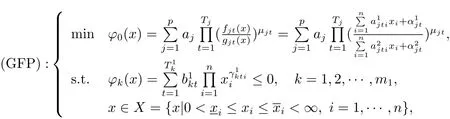
廣義分式規(guī)劃問(wèn)題是一類非凸優(yōu)化模型, 它包含比式和問(wèn)題、多乘積問(wèn)題、幾何規(guī)劃問(wèn)題等. 近年來(lái)這類問(wèn)題的特殊形式已經(jīng)引起許多學(xué)者的關(guān)注. 一方面, (GFP) 問(wèn)題通常存在多個(gè)非全局的局部最優(yōu)解, 在計(jì)算方面有很大的挑戰(zhàn). 另一方面, (GFP) 能廣泛應(yīng)用于實(shí)際問(wèn)題中, 如運(yùn)輸行業(yè)、政府合同、經(jīng)濟(jì)投資等[1–7]. 關(guān)于問(wèn)題(GFP) 的特殊形式, 文獻(xiàn)[8–11]中已給出不同的求解算法, 如分支定界算法、魯棒算法等. 本文針對(duì)一般形式的(GFP) 問(wèn)題提出一種迭代算法, 利用等價(jià)轉(zhuǎn)化技巧與特殊不等式的有關(guān)性質(zhì)將原問(wèn)題壓縮為幾何規(guī)劃問(wèn)題, 通過(guò)求解一系列幾何規(guī)劃問(wèn)題得到原問(wèn)題的解, 并對(duì)算法進(jìn)行理論分析, 通過(guò)數(shù)值算例表明提出的算法是可行有效的.

2 預(yù)備知識(shí)

為求解問(wèn)題(GFP), 引入變量ηjt, ξjt, 記

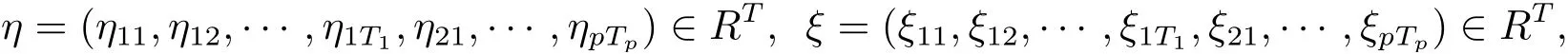
其中T = T1+T2+···+Tp. 并令aj> 0, j = 1,··· ,p1; aj< 0, j = p1+1,··· ,p. 問(wèn)題(GFP) 有如下等價(jià)形式

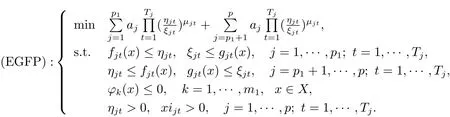
問(wèn)題(GFP) 和問(wèn)題(EGFP) 在如下意義下是等價(jià)的.

定理2.1如果(x?,η?,ξ?)是問(wèn)題(EGFP)的最優(yōu)解,則x?是問(wèn)題(GFP)的最優(yōu)解. 反之,如果x?是問(wèn)題(GFP)的最優(yōu)解,那么(x?,η?,ξ?)是問(wèn)題(EGFP)的最優(yōu)解,其中j =1,2,··· ,p; t=1,2,··· ,Tj.

證由問(wèn)題(GFP) 和問(wèn)題(EGFP) 的結(jié)構(gòu)易得結(jié)論成立.

基于以上討論, 為了獲得問(wèn)題(GFP) 的最優(yōu)解, 可以轉(zhuǎn)而求解其等價(jià)問(wèn)題(EGFP). 令z =(x,η,ξ)∈RN(N =n+2T). 通過(guò)改變記號(hào), 問(wèn)題(EGFP) 可被重新寫為如下形式

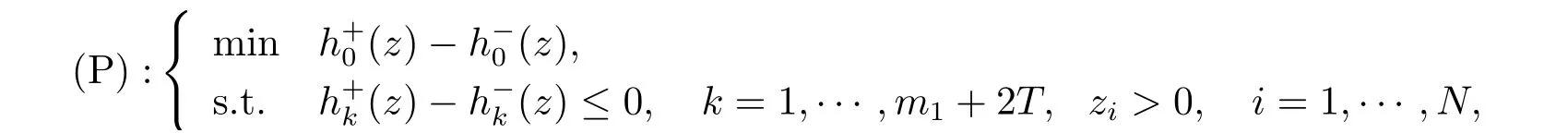
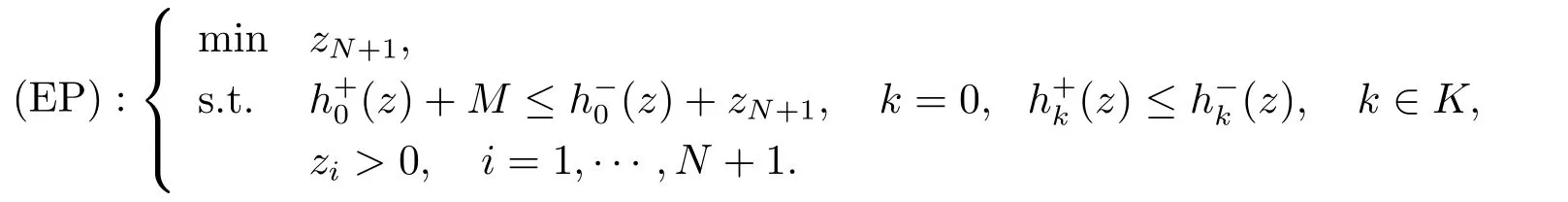
為了求解問(wèn)題(EP), 下面將提出一種迭代算法, 該算法通過(guò)求解一系列的幾何規(guī)劃來(lái)獲得問(wèn)題(EP) 的最優(yōu)解. 為此, 需要對(duì)問(wèn)題(EP) 中的約束進(jìn)行處理與變形, 當(dāng)k ∈K 時(shí), 根據(jù)的值將不等式約束分成如下兩類

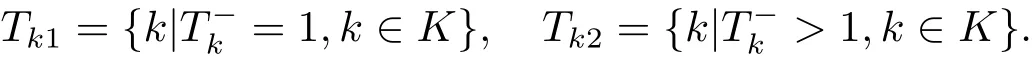
于是問(wèn)題(EP) 可以寫為如下形式

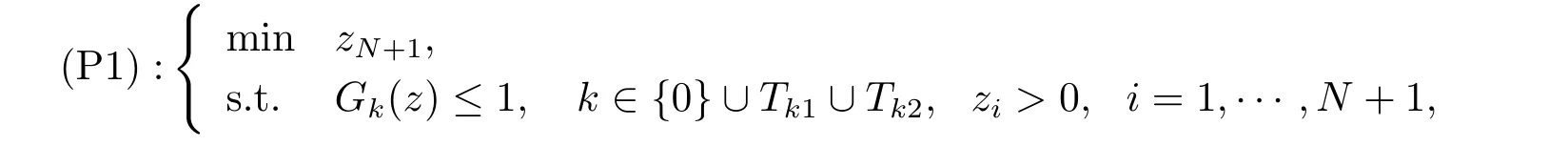
其中

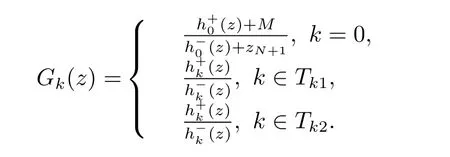
下面為了求解問(wèn)題(P1), 我們需要對(duì)問(wèn)題(P1) 中k =0,k ∈Tk2所對(duì)應(yīng)約束的右端項(xiàng)用近似單項(xiàng)式替換. 為此, 考慮如下函數(shù)

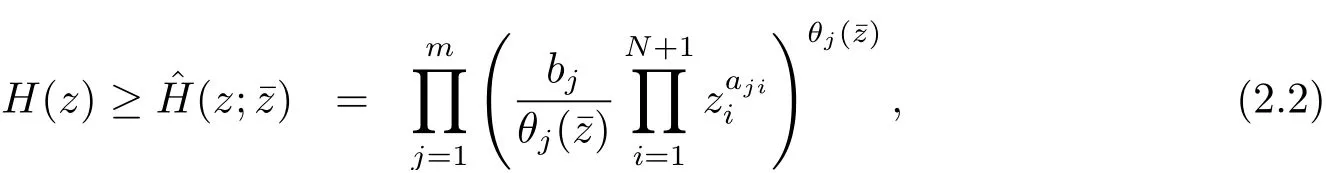
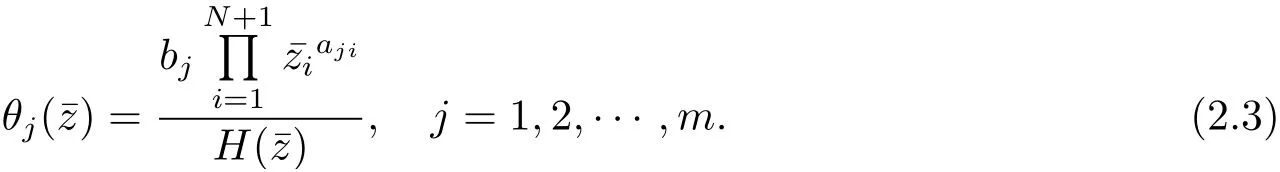
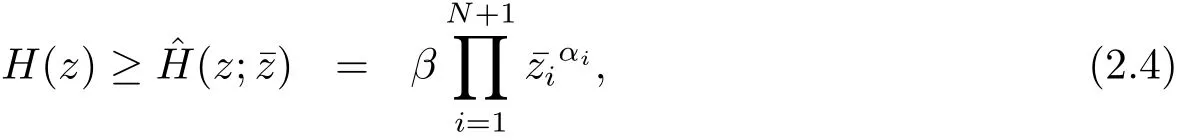
其中

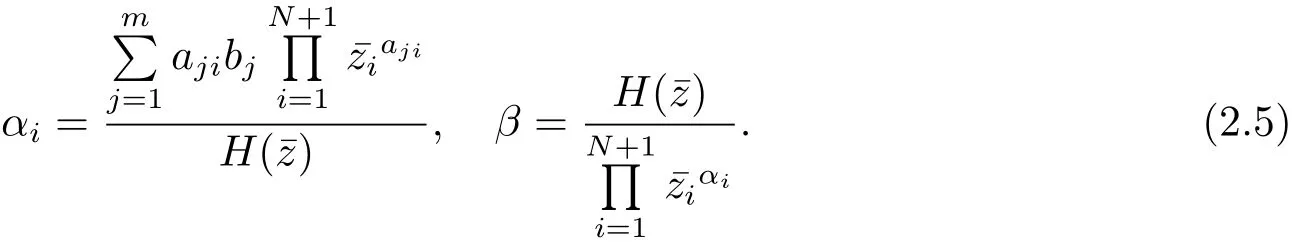
接下來(lái), 類似式(2.1)–(2.5) 的結(jié)果, 對(duì)于給定的點(diǎn)若k =0, 記

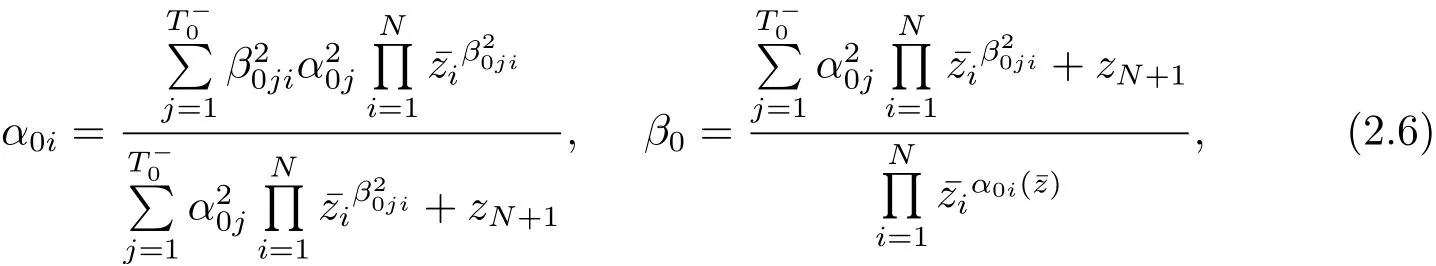
則有

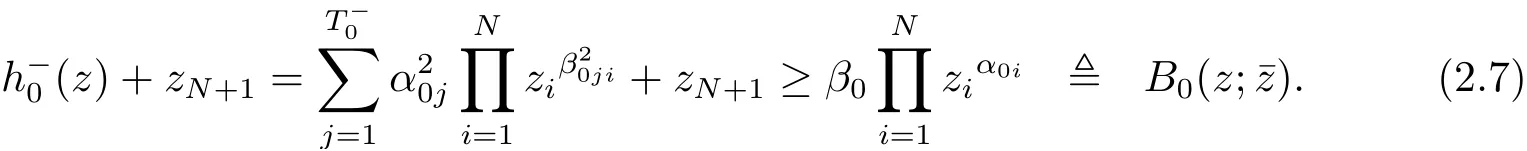
若k ∈Tk2, 記

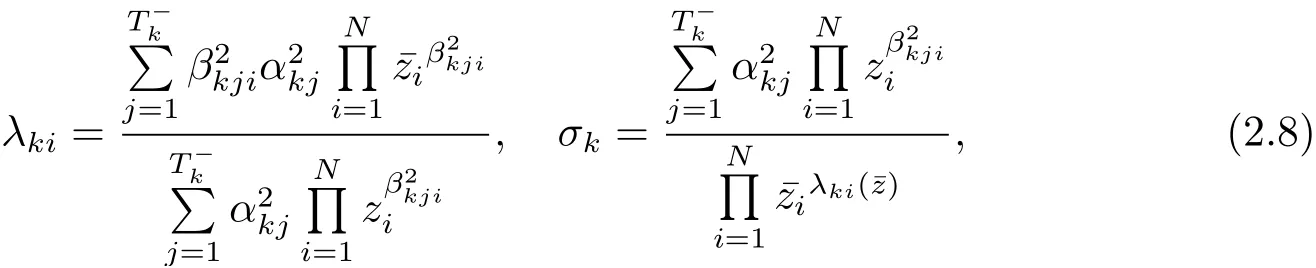
則有

因此問(wèn)題(P1) 可被壓縮為以下問(wèn)題

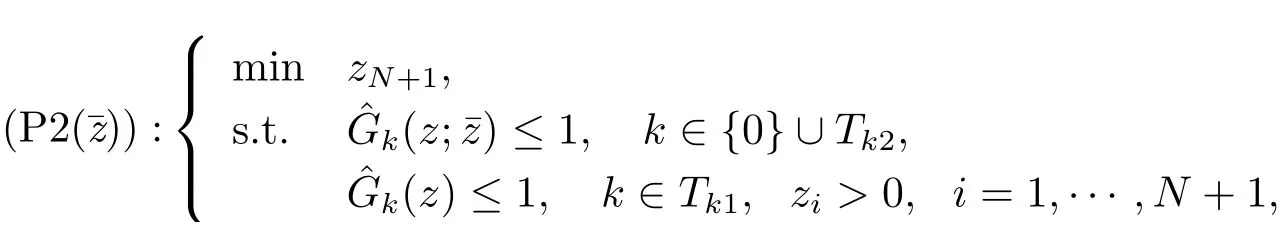
3 算法及其收斂性

根據(jù)上述討論, 問(wèn)題(GFP) 等價(jià)于問(wèn)題(P1). 給定點(diǎn)ˉz, 利用算術(shù)– 幾何平均不等式, 將問(wèn)題(P1) 壓縮為(P2(ˉz)). 為了獲得原問(wèn)題(GFP) 的最優(yōu)解, 這里提出一種迭代算法. 給定初始參數(shù)z0和誤差ε. 令ˉz =z0, 計(jì)算式(2.6), (2.8) 中的參數(shù)α0i,β0λki,σk, 可構(gòu)造幾何規(guī)劃問(wèn)題(P2(ˉz)), 求解(P2(ˉz)) 可獲得新的點(diǎn)z1. 若≤ε 成立, 算法終止, z?=z1即為問(wèn)題(GFP) 的近似最優(yōu)解. 否則, 令ˉz =z1, 重復(fù)上述過(guò)程直到滿足終止條件為止. 算法的具體步驟如下

步0給定容許誤差ε>0, 選擇初始點(diǎn)z0, 令迭代次數(shù)r =1.

步1令, 計(jì)算式(2.6), (2.8) 中的參數(shù)α0i,β0, λki,σk.

步2求解問(wèn)題得最優(yōu)解zr.

步3若≤ε, 算法終止. 令z?= zr, 且z?是問(wèn)題(P1) 的最優(yōu)解. 否則, 令r =r+1, 返回到步1.

算法的實(shí)際操作中, 若初始點(diǎn)為非可行點(diǎn), 那么算法經(jīng)過(guò)很少的迭代次數(shù)后就會(huì)產(chǎn)生問(wèn)題(P2的可行點(diǎn)[12]. 因此, 當(dāng)初始可行點(diǎn)未知時(shí), 可以用非可行點(diǎn)代替.

下面為了討論算法的收斂性, 先給出引理3.1.

引理3.1對(duì)于算法中產(chǎn)生的每一點(diǎn)zr(r ≥1) 均有

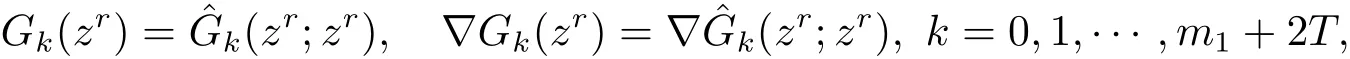
證由函數(shù)H(z),的定義以及代數(shù)平均不等式易得

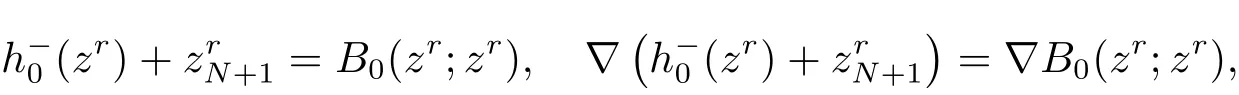
進(jìn)而由Gk(z),的表達(dá)式, 容易得出Gk(zr)=k =0,1,··· ,m1+2T.

當(dāng)k =0 時(shí), 對(duì)任意q =1,2,··· ,N +1, 有

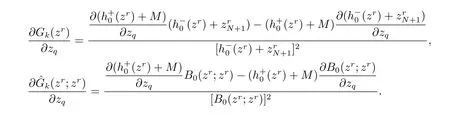
當(dāng)k ∈Tk1,k ∈Tk2時(shí),可類似證明. 從而

定理3.2對(duì)于算法中產(chǎn)生的點(diǎn)zr(r ≥1), 假設(shè)問(wèn)題(P2(zr)) 滿足Slater’s 約束規(guī)范.如果算法有限步迭代, 則算法終止于問(wèn)題(P1) 的KKT 點(diǎn). 否則, 如果算法產(chǎn)生無(wú)窮序列{zr}, 則無(wú)窮序列{zr} 的聚點(diǎn)是問(wèn)題(P1) 的KKT 點(diǎn).

證若算法迭代r 步后終止. 由于問(wèn)題(P2(zr)) 滿足Slater’s 約束規(guī)范, 則問(wèn)題(P2(zr?1)) 的最優(yōu)解zr是它的KKT 點(diǎn), 即有

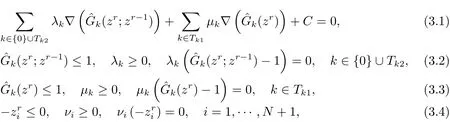
其中λk,μk,νi是拉格朗日乘子, C = (?ν0,?ν1,··· ,?νN+1+1)T∈RN+1. 另外, 由算法中的第3 步, 有zr=zr?1. 因此

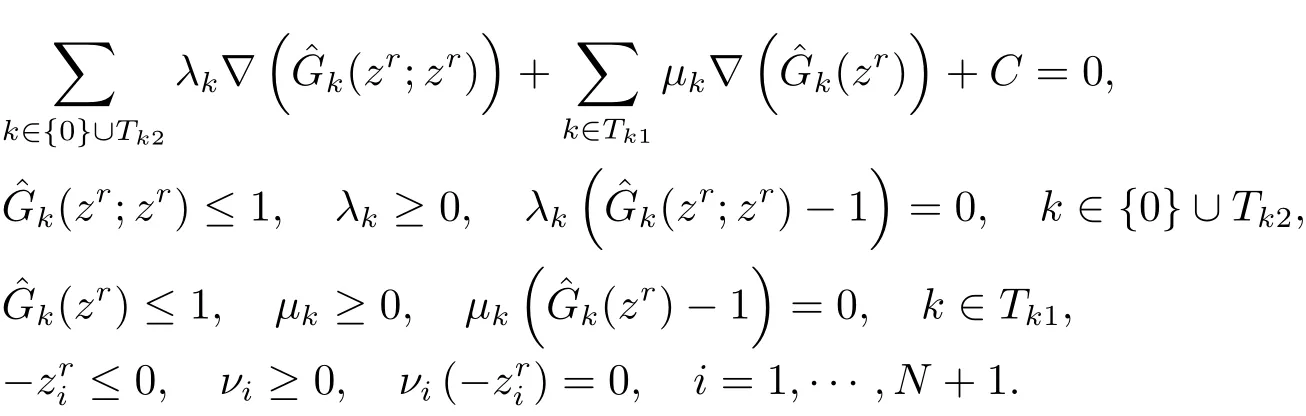
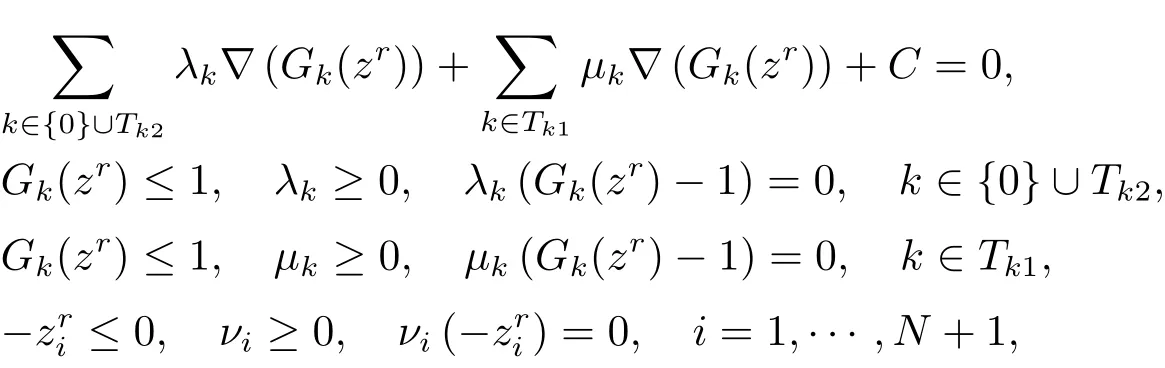
這意味著zr是問(wèn)題(P1) 的KKT 點(diǎn).

若算法是無(wú)限步迭代的, 易證序列{zr} 是有界的. 那么序列{zr} 存在一個(gè)收斂的子列.不失一般性, 仍記為序列{zr}, 并假設(shè)由和的連續(xù)可微性, 對(duì)式(3.1)–(3.4) 兩邊取極限, 可得

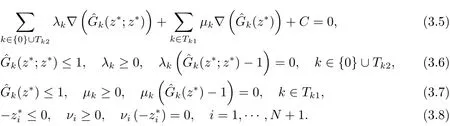
再結(jié)合引理3.1 和式(3.5)–(3.8), 有

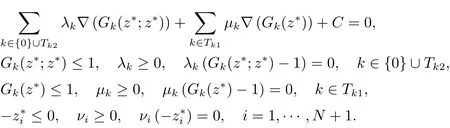
因此z?是問(wèn)題(P1) 的KKT 點(diǎn). 定理得證.

4 數(shù)值實(shí)驗(yàn)

為驗(yàn)證算法的有效性, 在酷睿雙核CPU (主頻2.4 GHz), 2GB 內(nèi)存的微機(jī)上用Matlab進(jìn)行數(shù)值計(jì)算. 表1 的數(shù)值結(jié)果表明本文算法是可行有效的.

例1

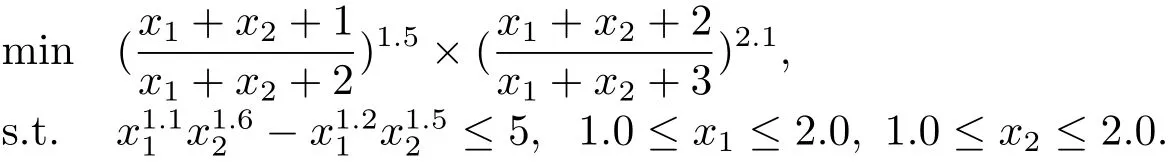
例2

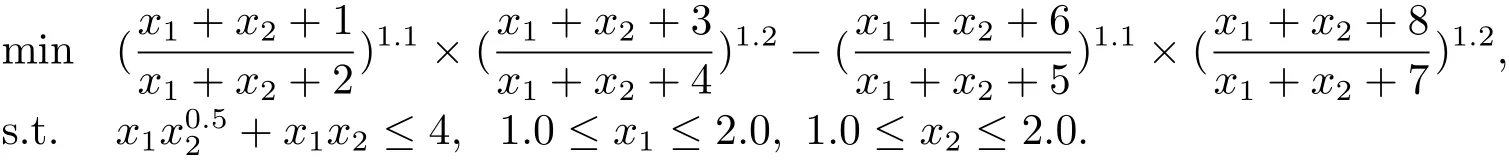
例3

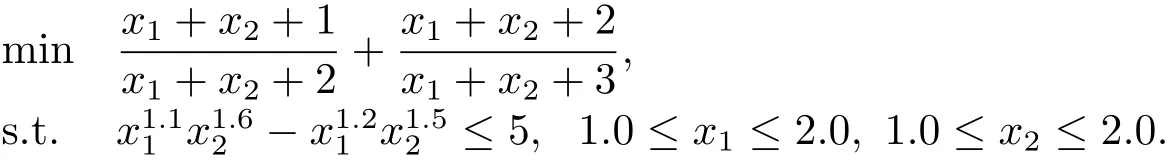
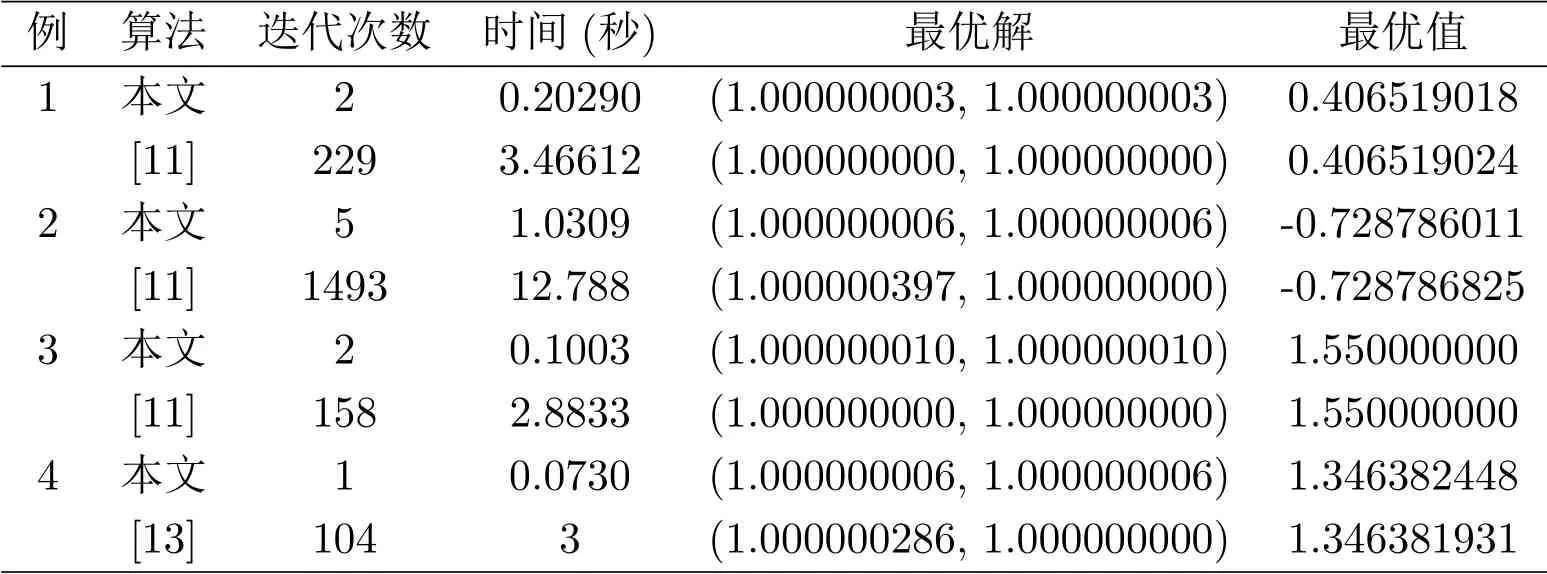
表1: 例1–4 的數(shù)值計(jì)算結(jié)果

例4

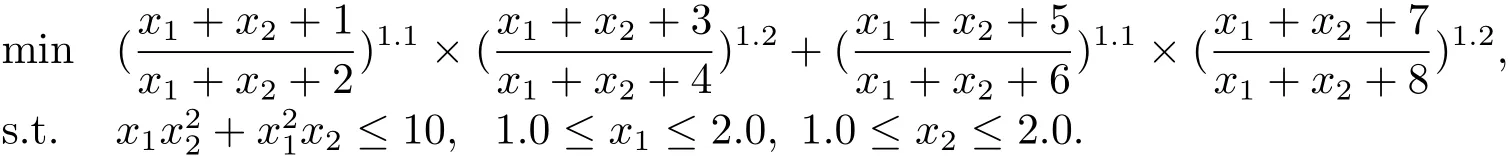
由表1 可知, 本文算法的運(yùn)行時(shí)間及迭代次數(shù)較文獻(xiàn)[11, 13] 都有明顯改善, 結(jié)果表明提出的算法是可行有效的.

5 結(jié)論

本文針對(duì)一類帶有多項(xiàng)式約束的廣義分式規(guī)劃問(wèn)題提出相應(yīng)的迭代算法, 利用等價(jià)轉(zhuǎn)化技巧與特殊不等式的有關(guān)性質(zhì)將原問(wèn)題的求解過(guò)程轉(zhuǎn)為一系列幾何規(guī)劃問(wèn)題的求解, 數(shù)值結(jié)果表明提出的算法是可行有效的. 另外, 本文考慮的問(wèn)題模型中要求fjt(x),gjt(x) 為正的仿射函數(shù), 但是本文算法針對(duì)更一般的模型也可以進(jìn)行求解.