帶粘性含不活潑項Cahn-Hilliard 方程解的存在性
徐紅梅,王一平
(河海大學理學院,江蘇南京211100)
1 簡介
帶粘性的含不活潑項Cahn-Hilliard 方程柯西問題形式如下:
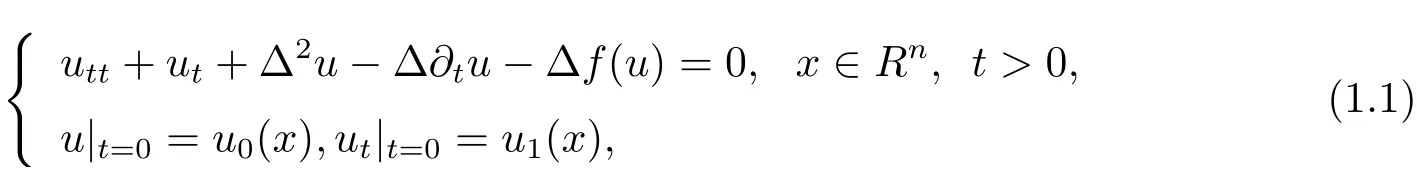
此處n 是空間維數, n ≥1; 未知函數u 表示一個相的相對濃度; 非線性項?f(u) 中f(u) 取成u2. (1.1) 式中若去掉utt???tu, 方程為

(1.2) 式是著名的Cahn-Hilliard 方程[1]. 近年來, Galenko 等[2?5]為模擬在某些玻璃中有深過冷產生的非平衡分解提出在(1.2) 式中加上不活潑項utt, 得

(1.3) 式詳細的物理背景可參看文獻[4–6]. (1.3) 式是一個帶松弛項的雙曲方程, 它在有限的時間內的不正則化導致很難得到其解的整體存在性. 對(1.3) 式, 前面的工作主要集中在弱解和擬強解. 如Grasselli 等[7,8]得到2 維和3 維情況下擬強解的存在性; Wang 和Wu[9]得到(1.3) 式在n ≥3 時小初值情況下經典解的存在性. 為克服不正則化困難, 在數學上經常是對方程加一粘性項, 增加耗散性, 如是得到(1.1) 式. 本文考慮(1.1) 式解的整體存在性.
本文中用C 表示常數, Lp(Rn), Hl(Rn) 表示通用的龍貝格可測函數空間和Sobolev 空間, 其模為
本文先分析(1.1) 式的格林函數, 再用壓縮映像原理證明(1.1) 式解的整體存在性.
2 格林函數分析
定義函數f 關于變量x 的傅里葉變換為
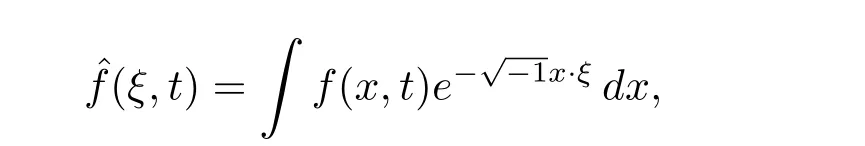
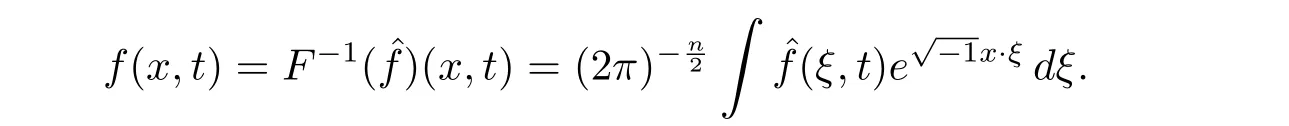
方程(1.1) 格林函數定義如下:
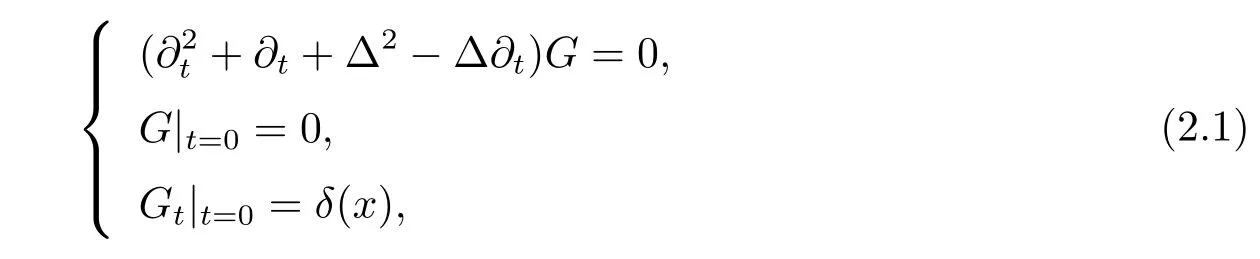
其中δ(x) 為常用Dirac 函數. 對(2.1) 式關于變量x 作傅里葉變換, 得常微分方程
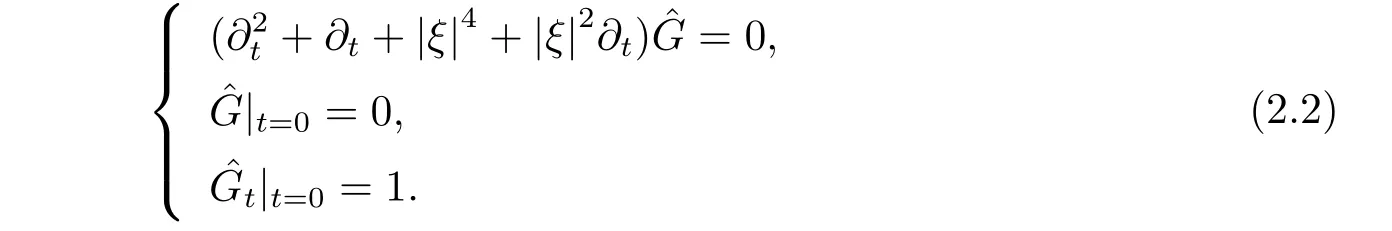
(2.2) 式的解為
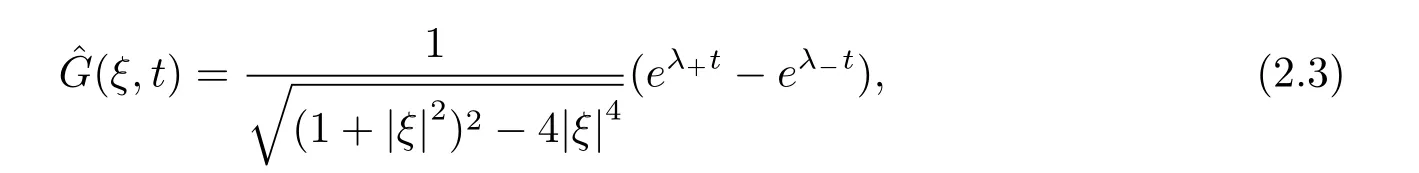
其中
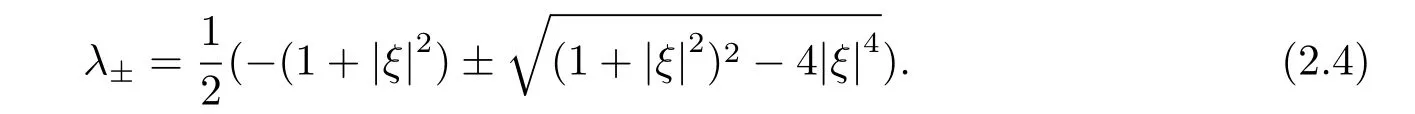
由(2.4) 式可知

當|ξ|2<1 時, 有
對于兩組患者的并發癥進行比較,觀察組患者出現皮下氣腫患者1例,出現腹部感染患者0例,出現泌尿系統感染患者2例,并發癥發生率為11.11%,對照組患者出現皮下氣腫,患者4例,出現腹部感染,患者3例,出現泌尿系統感染5例,患者并發癥發生率為44.44%,兩組之間比較差異明顯,P<0.05,具有統計學意義。
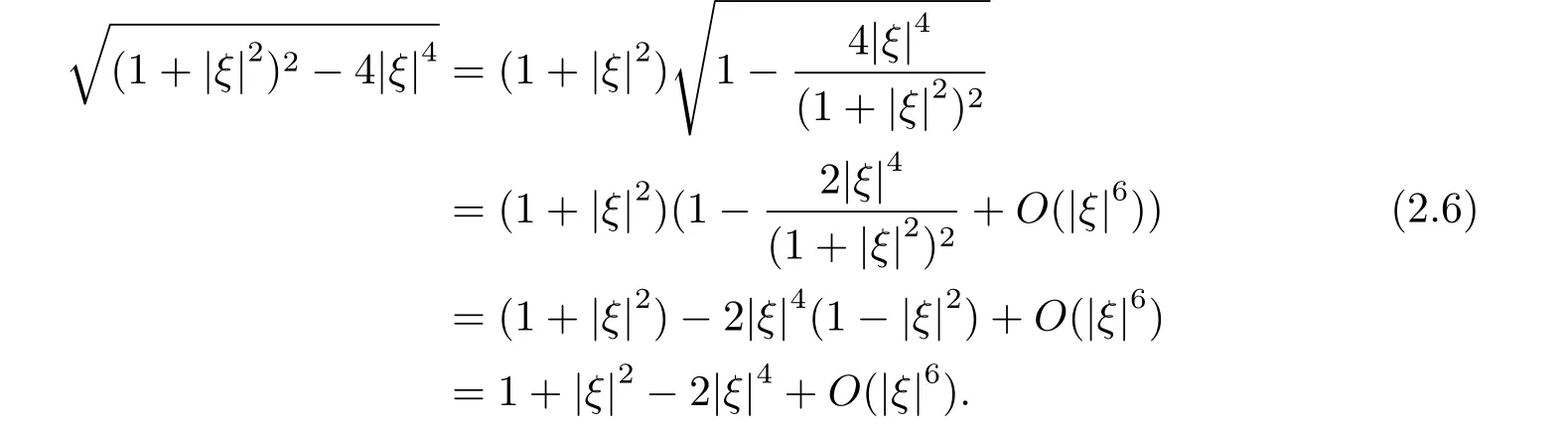
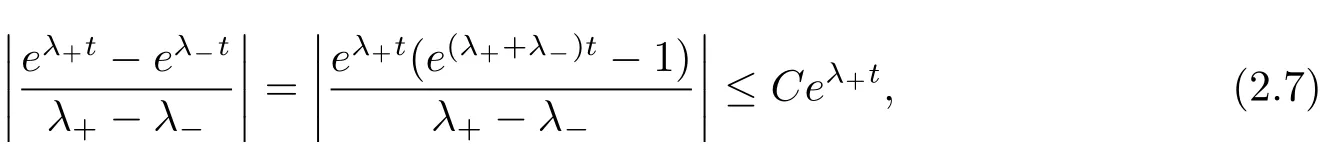

其中a>0. 當|ξ|2>1+ε 時,

由以上分析得到下述定理.
定理2.1對任意多重指標α, 存在常數Cα, 有

證由Plancherel 等式,
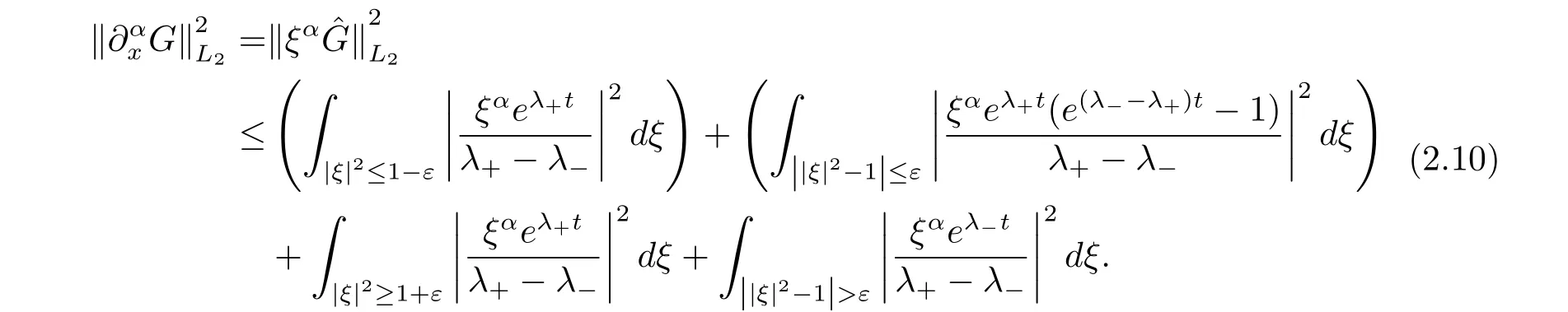
由(2.5) 式,

由(2.6) 式,
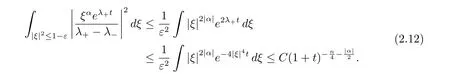
由(2.9) 式,

由(2.7), (2.8) 式得

因為
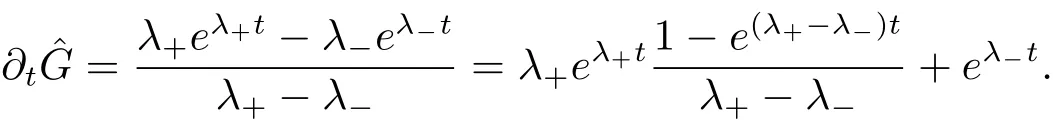
下面將由不動點定理證明(1.1) 解的存在性.
3 解的整體存在性
令
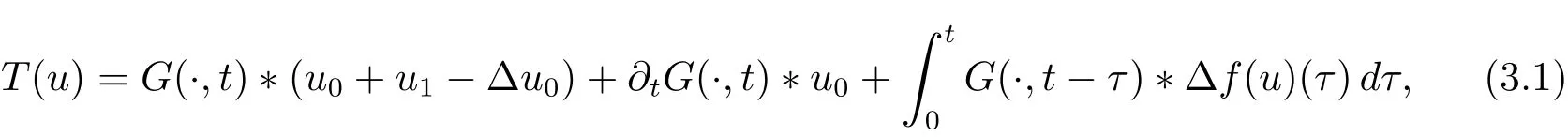
其中?是對變量x 的卷積.
定理3.1T 是從X 到X 的壓縮映射.
證由定理2.1, 當|α|≤1, 有
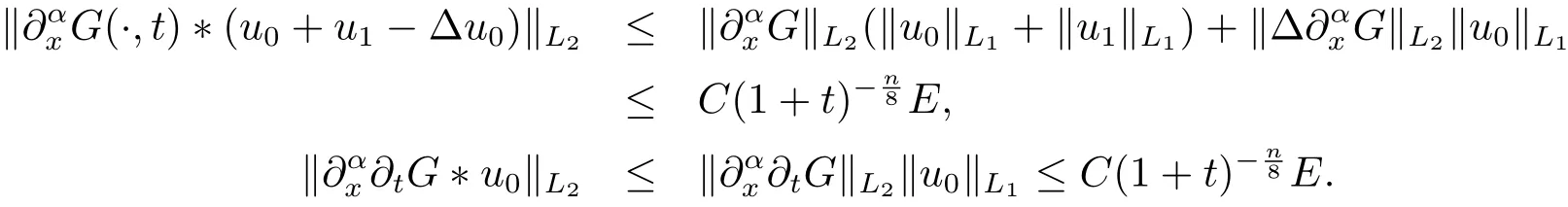
由定理2.1, Minkowski 不等式及f(u)=u2, 當|α|≤1, 有
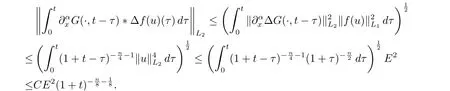
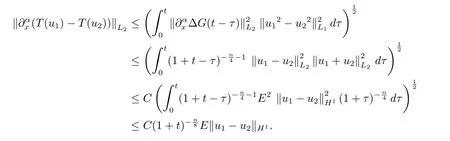
因為方程(1.1) 的解為u=T(u), X 又為完備度量空間, 于是得到本文結論.
定理3.2若u0,u1∈L1(Rn),則方程(1.1)有整體經典解存在,且u ∈L∞(0,+∞;H1(Rn)),

