簡化彈道設計方法在運載火箭型號論證中的應用
張博俊,王俊峰,李大鵬,肖 清
(北京宇航系統工程研究所,北京 100076)
運載火箭彈道設計是一種典型的非線性規劃問題,由于火箭的構型不同、目標約束不同,往往需要根據火箭構型進行多個控制變量的優化,計算工作量大。在運載火箭構型論證階段,需要根據可能的軌道、構型、發動機種類、加注質量進行組合,并在其中找到一個運載能力最大的構型,工作量非常大。同時,由于構型不同,火箭的控制變量也不盡相同,難以進行統一建模,往往需要根據具體軌道、構型進行精細設計才能得到最優運載能力。因此,有必要針對運載火箭彈道設計問題進行分析、簡化,構建一種通用的、易于尋優的簡化彈道設計方法,滿足減少運載火箭構型論證工作計算量的需求。
張子明等[1]探討了運載火箭上升段的主要優化參數。張柳等[2]在此基礎上提出了一種基于PSO-Powell算法的運載火箭優化算法,認為影響火箭運載能力的主要變量為各級程序角。胡冬生等[3]分析了不同約束變量對火箭運載能力的影響。洪蓓等[4]提出了在有入軌約束的情況下進行運載火箭彈道優化的算法。熊偉等[5]提出了一種利用遺傳算法和牛頓迭代法共同對彈道參數進行尋優的方案。這些方案都提出了一系列針對固定構型的運載火箭彈道優化思路。本文根據對多種構型火箭不同發射軌道的研究,提出了一種簡化彈道設計方法,解決在構型論證工作中運載火箭的運載能力優化問題,極大地減少了計算量。該方法通過簡化入軌級程序角設計方法使不確定的非線性規劃問題轉化為一次牛頓迭代尋優過程,提高了計算效率。通過對國內外的2種運載火箭的飛行曲線擬合,驗證了該方法的可行性和正確性,證明了簡化彈道設計方法可以滿足構型論證工作中由于軌道、構型不確定產生的統一彈道計算方法的需求。
1 彈道計算的數學模型
1.1 動力學模型
建立在發射坐標系下的火箭的上升段彈道三自由度質點動力學方程[6]:
(1)
(2)
(3)
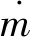
1.2 飛行程序角模型
在文獻[2]的基礎上對飛行程序角進行一定的修改,公式分為3部分,其中前兩部分全稱為重力轉彎段,該段的飛行程序如下:
(4)
式中:α為攻角,θ為彈道傾角,ωz為地球旋轉角速度在發射坐標系z軸方向的分量,tturn為垂直段飛行時間,則
α=4αMetturn-t(etturn-t-1)
(5)
式中:αM為常量,也是迭代參數。
根據式(4)、式(5)可以得知,火箭的重力轉彎段分為2個過程,一個是從t0到tturn的垂直起飛過程,該時間可以由火箭出發射塔時間計算得出;另一個是重力轉彎過程,在這一階段,攻角α的曲線由期望的關機點程序角終值迭代αM得出,并最終計算得出飛行程序角。
轉彎段關機后至停泊軌道為第3個部分,該段程序角為
(6)
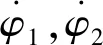
(7)
1.3 推力啟動段關機段的簡化
在實際火箭飛行過程中,必須考慮到火箭每一級發動機啟動段的推力、流量的建立、關機過程,情況較為復雜。同時,由于冷熱分離情況不同,因此在實際的火箭彈道計算過程中,發動機推力的建立和關機是必須詳細考慮的。另一方面,推力、流量的曲線并非線性變化的,不同推進劑的發動機的啟動、關閉時間也不相同,因此很難用一個框架來統一化處理。
經過大量分析,由于發動機啟動、關閉階段的總時間較短,提供的總沖量相對于整個飛行過程來說極小,因此可以直接將這一部分略過,認為這一部分的流程直接可以產生標稱的推力,不計算啟動關機過程,改為由節流時間和節流程度來模擬啟動、關機過程。
因此,推力公式可以改寫為
(8)
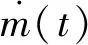
(9)
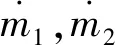
2 迭代模型的通用化處理
在構型論證階段,由于火箭構型未定,因此在進行設計的時候很難固定參考某一在飛型號進行彈道優化設計,因此有必要針對優化算法進行通用化處理,使程序能夠適應大多數在飛、在研的火箭構型。
2.1 火箭彈道設計模式
目前在飛的火箭構型主要有以下幾種:
①光桿構型。無助推,可能有兩級火箭或者三級火箭。
②助推構型。有助推,可能有兩級火箭或者三級火箭,各芯級關機時間有可能與助推相同或者延后。
③火箭加上面級狀態。在上述2種火箭的基礎上加上上面級,由上面級帶衛星直接入軌。
而入軌的軌道有以下幾種:
①直接入軌型太陽同步軌道(sun-synchronous orbit,SSO)、近地球軌道(low earth orbit,LEO),無滑行狀態,火箭直接進入目標軌道;
②霍曼轉移入軌,需要在基礎級或者一級/二級飛行完成后,由入軌級滑行一段時間到達原地點后點火進行軌道圓化。
可見,經過排列組合后,構型論證需要面對的工況數量龐大,而且難以固定一種設計方法進行彈道計算。因此有必要針對這種情況進行統一的彈道設計方法建模,適應不同的情況。
2.2 彈道整體分段
一般來說,可以認為霍曼轉移入軌是在火箭進入一個稍小的圓形或者橢圓軌道后,再滑行一段時間到指定位置,發動機二次啟動進入目標軌道的過程[8]。很明顯,在第一步的彈道設計中,設計過程是相同的。因此,在這里將計算流程整體分為2種狀態:非滑行狀態和滑行狀態。非滑行狀態是指火箭直接入軌各種軌道;滑行狀態是指在非滑行入軌后,再增加滑行段和最終入軌段。
由于目前的火箭動力水平達不到單級入軌,直接入軌彈道至少需要兩級才能入軌,所以,可以設計第一段彈道為重力轉彎彈道,后續段為入軌彈道。
重力轉彎彈道在文獻[9]中有具體的設計方法描述,在這里不再展開。重力轉彎后,一般助推或一級將進行分離,而為了提高運載能力,一級/二級等將會多飛一段時間,這一段的工作級的數量是不一定的,有可能是單二級工作(Falcon9),也有可能是一級、二級一起工作(CZ-7)或者一級、二級、三級一起工作(CZ-3B)。各類火箭的構型不同,彈道設計時的設計變量也不相同,因此不能以火箭工作級作為俯仰程序角的設計分段。
針對這種情況,可以將火箭第一次關機作為重力轉彎段終止點,將后續直到入軌的各段統一作為一段真空推力段來進行設計,并將這一段稱為入軌段。這樣,可以將重力轉彎段后未知的火箭級數統一起來,認為是由一個程序角變化率和對應的飛行時間控制的飛行段。該段的主要任務是控制火箭從重力轉彎段后到入軌的這一段的飛行軌跡。
2.3 非滑行狀態設計方法
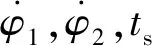
在實際彈道設計過程中,首先估計一個轉彎段俯仰程序角終值φ0,這樣就決定了本次計算時入軌段的起點,然后使用入軌段的3個控制參數進行迭代設計達到入軌要求,流程如下。
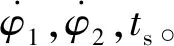
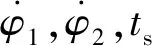
(10)
(11)
解完方程組后,即可得到能夠滿足從轉彎段終點到入軌點的一組控制變量。
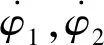
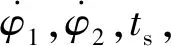
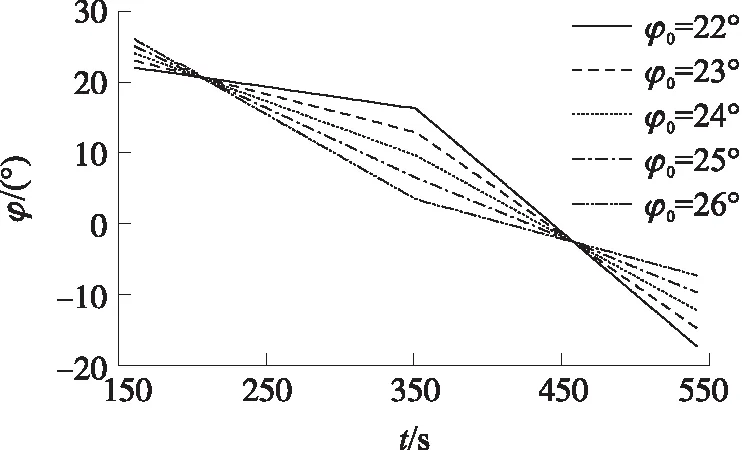
圖1 不同φ0對后續程序角的影響
運載能力曲線如圖2所示,圖中,mt為載荷質量運載能力。由圖2可見,不同的φ0對應的運載能力是一條反拋物線,可以解出極值。
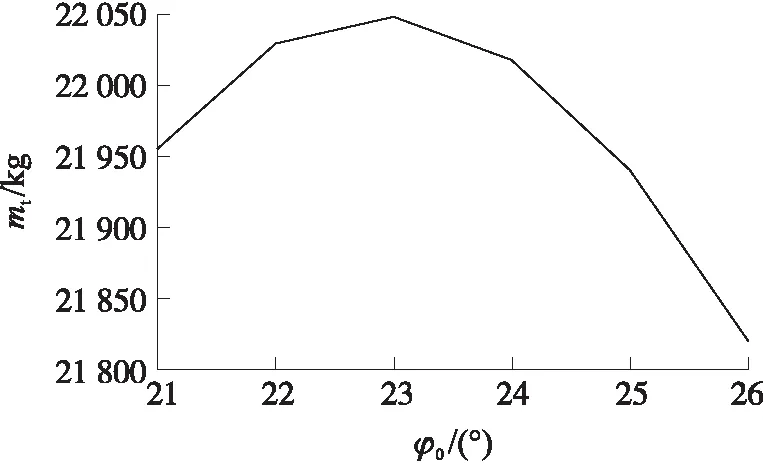
圖2 不同φ0對應的最優運載能力
可見,在不同的重力轉彎段程序角終值φ0的情況下,運載能力明顯成反拋物線型,因此可以使用牛頓迭代算法對φ0進行尋優,即可找到最優運載能力。
2.4 滑行狀態
針對上面級入軌或霍曼轉移入軌計算時,可以將2.3節計算完的最優停泊軌道作為計算的初始狀態,并增加一段無動力滑行段和一段動力段,實現運載火箭從停泊軌道到目標軌道的轉移。一般來說,僅需要進行一次工作就可以滿足入軌要求,因此設計思路更加簡化。
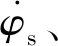
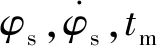
③重復計算至滿足入軌要求。
這樣就可以在原本的停泊軌道的基礎上,計算出SSO或GTO軌道的運載能力,完成了構型論證的驗證。
綜上所述,通過分析非滑行入軌和滑行入軌的2類軌道設計流程及不同火箭構型的設計思路,將非滑行入軌彈道設計抽象為2段入軌設計思路,對設計流程進行了簡化。將復雜的、不確定非線性規劃問題簡化為對轉彎段程序角φ0的梯度尋優過程,極大地簡化了彈道設計的復雜度。
3 模型驗證
為驗證簡化模型在不同構型火箭、不同發射任務中的應用效果,選取了美國SpaceX公司的Falcon9火箭發射銥星任務和典型CZ-3B火箭發射任務進行復算。
3.1 CZ-3B改進型火箭
使用簡化模型后,計算長三甲系列火箭用戶手冊中的典型CZ-3B火箭任務軌道參數,計算運載能力結果為5 510 kg,手冊中給出的運載能力為5 500 kg,二者極為接近。表1對比了手冊及簡化彈道設計方法計算出的主要動作時序。由于CZ-3B火箭一級、二級屬于熱分離,因此時間偏差較小,到三級第一次關機后,由于簡化模型未計算后效等方面的影響,累計了一些時間偏差,但啟動段、關機段沖量較小,未對運載能力產生較大影響。
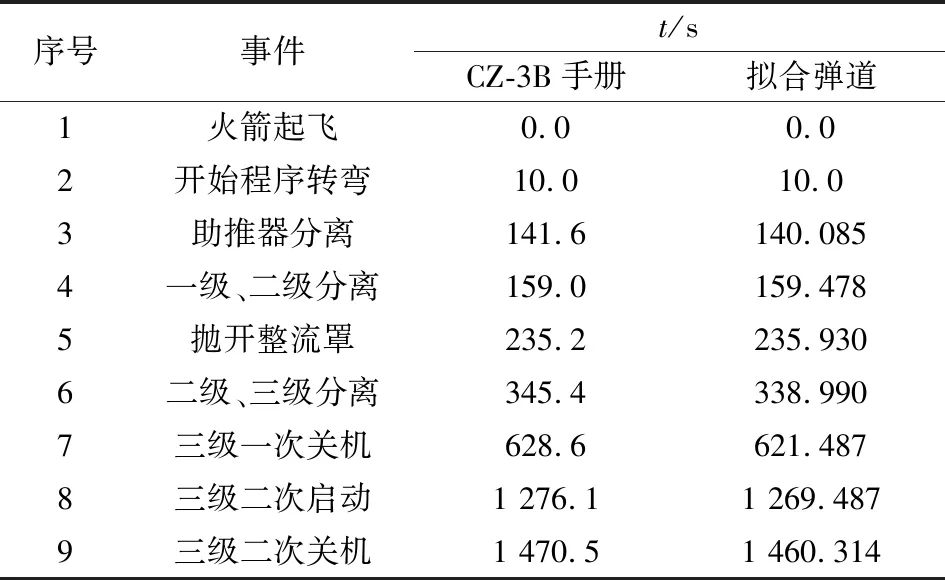
表1 CZ-3B典型任務時序對比
圖3顯示了簡化彈道設計方法計算出的運載火箭速度、高度曲線與CZ-3B典型發射任務的速度、高度曲線的對比情況,由圖可見,二者十分接近。
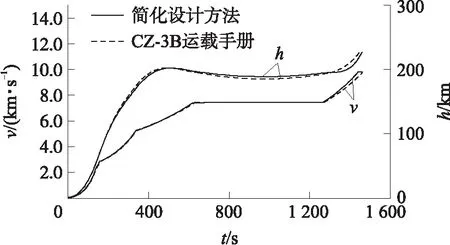
圖3 CZ-3B速度、高度對比曲線
圖4為使用簡化彈道設計方法后計算得出的CZ-3B火箭飛行程序角。
3.2 Falcon9火箭
Falcon9火箭參數來自SpaceX官網,根據發射任務手冊,本次Falcon9火箭發射任務載荷為9.6 t,使用簡化彈道設計方法計算后,得到運載能力為9.69 t,二者差距較小,一級、二級主要動作時序見表2。由表2可見,由于參數資料較少,實際飛行時間有一定的偏差,但各分段時間差異不大。
表2給出了Falcon9銥星任務實測飛行時序與擬合彈道的對比情況。
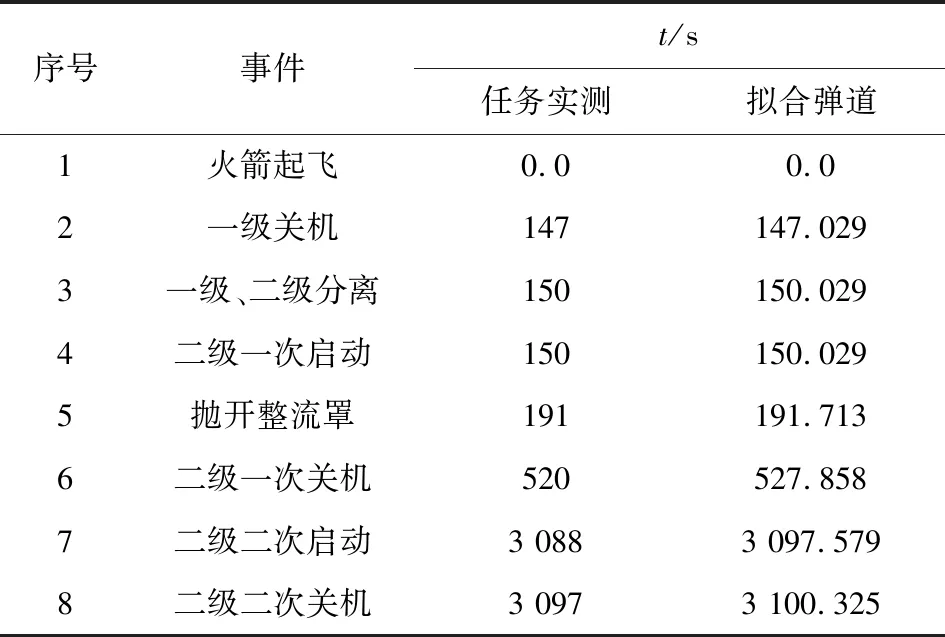
表2 Falcon9銥星任務時序對比
圖5給出了簡化彈道設計方法計算出的Falcon9銥星任務的速度、高度曲線,并與該任務視頻中給出的速度、高度曲線進行了對比。由圖可見,通過簡化彈道設計方法計算得出的擬合彈道與實際飛行數據貼近,擬合效果較好。
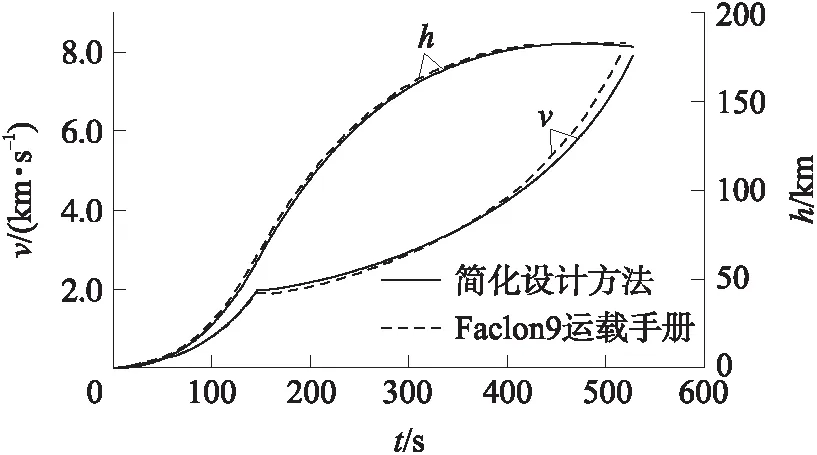
圖5 Faclon9速度、高度對比曲線
圖6中給出了Falcon9銥星任務使用簡化彈道計算方法得出的飛行程序角。
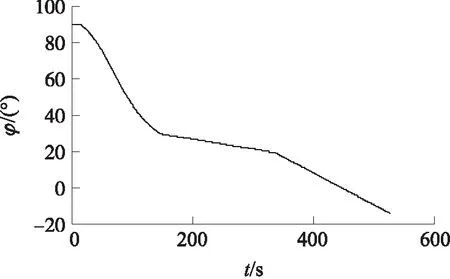
圖6 Falcon9銥星任務飛行程序角曲線
由CZ-3B、Falcon9 2種構型的火箭運載能力計算、實測數據比對可以看出,簡化彈道模型通過較少的輸入參數、更簡單的控制變量和計算方法即可達到很高精度的彈道復現,證明了簡化彈道設計方法的可行性。
4 結論
通過理論分析,本文對現有的彈道計算模型進行了簡化,極大地減少了輸入數據的類型和數量,并將不確定的非線性彈道設計問題簡化為梯度尋優過程。使用簡化彈道設計方法對CZ-3B、Falcon9 2種構型完全不同的現役運載火箭的實際飛行曲線進行了擬合,對比結果顯示,盡管存在一定的偏差,但整體上曲線復現效果較好,運載能力接近,證明了簡化彈道設計方法的可行性、正確性。因此,可以認為簡化彈道設計方法可用于構型論證階段的彈道計算。

