回轉式彈倉的自適應近似變結構控制

王 鍇,尹 強,羊 柳

(南京理工大學 機械工程學院,江蘇 南京 210094)

回轉式彈倉對于火炮自動裝填系統來說是十分重要的一個分系統,回轉式彈倉通過永磁同步電機提供動力源,在電機的旋轉下通過減速箱帶動彈倉的鏈條轉動,將待射擊彈丸旋轉至取彈口。如果彈倉控制精度低將導致機械手取彈失敗,造成安全隱患,因此彈倉的工作性能將直接影響火炮自動裝填系統能否順利完成射擊任務。因此,提升回轉式彈倉的控制精度并降低其在運動過程中的振動將存在重要意義。回轉式彈倉由彈筒、鏈輪、鏈條、導軌、基座等組成,是一類具有大慣量變化及系統參數具有不確定性特點的系統,其運動控制具有一定的難度。鄒權等[1]提出了一種帶有積分型滑模面的自適應魯棒控制算法,在理論上證明了其提出的算法具有更好的動態性能及穩態性能。侯保林等[2]提出了一種基于線性矩陣不等式(LMI)的魯棒控制算法,即最優保性能控制算法,并驗證了算法具有高的控制精度。岳才成等[3-4]針對鏈式彈倉提出了一種基于指數趨近律的滑模控制方法,引入模糊自適應算法,實現了系統的精確定位,有效抑制了趨近過程的振動。李杰等[5]針對非線性自抗擾控制在實際應用中的困難等問題,提出了一種線性/非線性自抗擾控制切換控制方法,解決了非線性自抗擾控制在參數整定、穩定性分析等方面的困難。薛生輝等[6]針對比例-積分控制因不能預測未來輸出而提前改變控制量,從而在用于光電穩定伺服系統時往往響應劇烈的問題,提出了一種新型的基于PI(比例(proportion)、積分(integral))增量和GPS增量加權的比例積分控制加廣義預測控制算法,實現了基于歷史、當前和未來偏差計算控制量,通過仿真驗證了該方法的精度、平穩性及快速性。鄭美茹等[7]針對永磁同步電機的傳統滑模控制技術中趨近速度與振動程度之間存在矛盾的問題,利用分數階積分型符號函數的特性,設計基于分數階的積分時變滑模變結構控制器,達到了在振動程度較小的前提下提高系統響應速度的目的,仿真和實驗結果證明了該方法的強魯棒性及快速性與準確性。葉鐳等[8-9]針對炮控系統不確定性參數,提出了一種基于自抗擾控制的解耦方法,這種方法能夠有效抵抗系統的不確定非線性因素,并驗證了其強魯棒性和有效性。上述文獻中所提出的控制算法均取得了比較滿意的控制效果,在以上研究成果的啟發下,本文針對火炮彈倉運動過程中彈倉出現振動、控制精度不高、非線性摩擦以及沖擊等問題,提出一種改進自適應近似變結構控制算法(improved adaptive approximation variable structure,IAAVS)以提高控制精度并降低系統振動。

滑模變結構控制表現出強魯棒性,利用滑模變結構控制對系統參數擾動不敏感的特性,可以提高控制系統的性能[10]。但是,一般的變結構控制律都是不連續的,從而不可導。控制信號的不連續是由控制律中所含繼電控制項引起的,易形成控制信號的顫振,具有不連續控制律的滑模變結構控制在實際使用中不易實現,并且影響控制系統的使用壽命。本文用連續可導的控制律替代傳統滑模不連續可導控制律,運用自適應算法,依據系統狀態進行切換函數的自適應改變;在運動規劃方面引入三角函數規劃法,使規劃運動的軌跡連續光滑且連續可導。仿真結果表明,該方法具有很高的控制精度,并且明顯降低了振動。

1 系統描述與數學建模

回轉式自動化彈倉由永磁同步電機提供動力,永磁同步電機采用力矩控制方式。鑒于電機本身的設計特點,本文忽略電流環影響,不再考慮電機內部對電機控制的影響。由于彈倉系統構件繁多,對其進行合理化簡化,將彈倉系統所有構件視為剛體,將彈倉運動過程中的物理參量等效到永磁同步電機的轉子軸上,取電機轉子為等效構件,系統動能方程為

(1)

式中:Jeq為系統的等效轉動慣量;Ja為永磁同步電機轉子的轉動慣量;Jb為減速箱的等效轉動慣量;Jci和ωci分別為第i個鏈輪的轉動慣量和角速度;x為鏈輪總數;ω為永磁同步電機轉子實際角速度;Jdj和ωdj分別為第j個彈筒(含彈丸)的轉動慣量和角速度,n1為旋轉運動彈筒(含彈丸)的個數;mdk和vdk分別為直線運動的第k個彈筒(含彈丸)的質量和質心速度,n2為直線運動的彈筒(含彈丸)的個數;Jef和ωef分別為第f個鏈節的轉動慣量和角速度,x1為旋轉運動鏈節的個數;meβ和veβ分別為第β個作直線運動的鏈節的質量和質心速度,x2為直線運動鏈節的個數。對式(1)進行化簡,得:

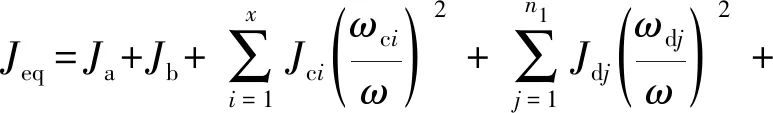
(2)

在運動過程中,回轉式彈倉各部件之間會產生一定的阻尼力,現將系統阻尼力等效到永磁同步電機的等效轉子上,得到等效力的方程:

(3)

式中:Beq為系統的等效阻尼系數;Ba為同步電機的等效阻尼系數;Bb為減速箱的等效阻尼系數;Bci,θci分別為第i個鏈輪的阻尼系數、電機轉子轉動一圈時鏈輪的角位移;Bdj,θdj分別為第j個彈筒(含彈丸)的黏性阻尼系數、電機轉子轉動一圈時的角位移;Ddk,Ldk分別為第k個做直線運動的彈筒(含彈丸)的黏性阻尼系數、直線位移;Bef,ωef,θef分別為第f個鏈節的黏性阻尼系數、角速度、電機轉子旋轉一圈時的角位移;Deβ,veβ,Leβ分別為第β個做直線運動的鏈節的黏性阻尼系數、速度以及位移。對式(3)進行化簡,得:

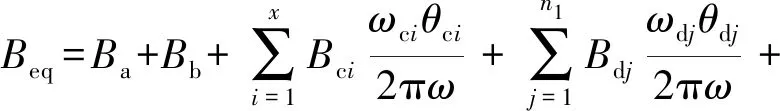
(4)

回轉式自動化彈倉的動力學方程為

(5)

圖1 期望軌跡

2 改進的自適應近似變結構控制

定義系統的位置跟蹤誤差e:

e=θ-θd

(6)

式中:θd為彈倉實際角位移。

對于設計的有界的控制輸入,實驗的目標就是使電機轉子的位移θd能夠很好地跟蹤期望軌跡的位移曲線θ,且產生的跟蹤誤差盡量小,以提高系統性能。

本文中,切換函數采用積分型滑模函數,并采用自適應算法對切換函數進行改變,定義滑動超平面Q:

(7)

式中:A為待定系數,λ為滑模面參數,且A>0,λ>0。

由式(5)、式(6)和式(7)得:

(8)

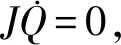
(9)

由于系統的不確定擾動不可能為0,遂增加切換控制項us以平衡系統的不確定擾動,切換控制項為

us=-ηsgns

(10)

式中:η為切換項增益,且η>0,sgns為符號函數,定義如下:

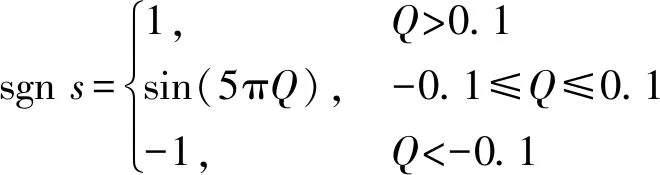
(11)

同時為了提高系統的控制穩定性,增加魯棒控制項uk:

uk=-yQ

(12)

式中:y為待定系數,且y>0。

得系統的控制律u:

(13)

穩定性分析,定義Lyapunov函數V1:

(14)

將式(14)對時間求導,并將式(6)、式(8)、式(13)代入,得:

(15)

根據式(10),存在合適的A,y,η使得式(15)為

(16)

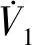
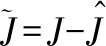
(17)

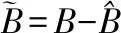
(18)

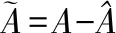
(19)

所以系統的控制律改寫為

(20)

定義如下的Lyapunov函數V2:

(21)

式中:γ1,γ2,γ3為待定系數,且γ1>0,γ2>0,γ3>0。將式(18)對時間求導,并將式(17)的控制律u代入得:

(22)

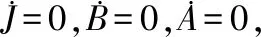
(23)

將式(20)代入式(19),得:

(24)

即可設計合適的系統參數使得系統具備達到滑模面的條件并保持穩定。

3 仿真分析與驗證

由于彈倉系統攜帶彈丸數量比較多,彈丸數量變化情況多,所以本文只對3種情形進行研究,即空載(彈筒不裝彈丸)、半載(裝載一半彈丸且相鄰排列)、滿載(彈筒內全部裝載彈丸),不同載荷條件下的等效轉動慣量J與等效阻尼系數B如表1所示。

表1 等效轉動慣量及等效阻尼系數

從圖2可以得出:改進后的自適應近似變結構控制器與傳統自適應滑模控制器的位置跟蹤誤差幾乎為0,控制效果明顯優于PID控制器的跟蹤效果;PID的控制誤差維持在-0.121～0.1 rad。現將改進后的自適應近似變結構控制與傳統自適應滑模控制器的位置跟蹤效果進行放大對比,結果如圖3所示。從圖3可以得出,傳統的自適應滑模控制的位置控制誤差在系統起始階段出現小幅振動。圖3(b)為仿真曲線的局部放大圖。在整個過程中振動比較劇烈且位置誤差收斂在-2.5×10-4～2.5×10-4rad;改進自適應近似變結構控制在系統初始階段控制誤差為0,在加入等效擾動以后,位置誤差出現很小的波動,且曲線較平滑,將位置誤差保持在-1.31×10-4～1.31×10-4rad之間,位置控制效果明顯優于傳統自適應滑模控制,這表明改進后的自適應近似變結構控制,通過運用連續控制律代替傳統不連續控制律并且對切換函數進行自適應調整的方法,在位置跟蹤誤差方面具有明顯的優勢以及降低振動的效果。

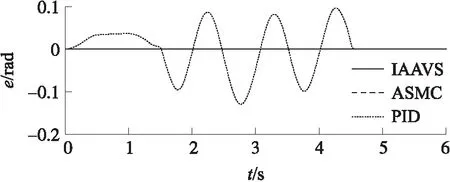
圖2 3種不同控制方法(滿載)同種工況下控制誤差對比

圖3 IAAVS與ASMC同種工況下控制誤差對比

圖4為回轉式彈倉在分別應用PID、ASMC與IAAVS 3種控制方法時控制輸入u的對比圖。從圖4(b)中可以得出,回轉式彈倉在應用ASMC控制方法時,控制輸入u出現了明顯的振動現象;從圖4(a)中可以得出,回轉式彈倉在應用IAAVS、PID 2種控制方法時,彈倉的控制輸入u曲線相對ASMC控制輸入u更加平滑,未出現振動現象。因此,結合位置跟蹤誤差e曲線與控制輸入u曲線可以得出,改進自適應近似變結構控制方法更適用于回轉式彈倉的定位控制,有效降低了彈倉位置跟蹤誤差,降低了彈倉控制輸入u的振動,具有很好的魯棒性及精確性。

圖4 3種不同控制方法(滿載)同種工況下控制輸入u

圖5為回轉式彈倉空載、半載、滿載時位置控制誤差對比。從圖5可以看出,彈倉在空載、半載、滿載3種狀態下的位置跟蹤誤差基本相同,誤差保持在-1.5×10-4～1.5×10-4rad之間,說明了本文所提方法對于不同載荷條件下的彈倉運動控制具有很好的一致性,仿真結果滿足系統對于誤差的要求。

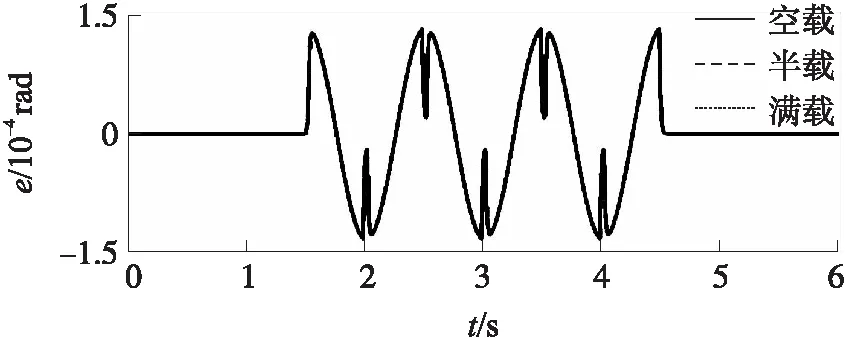
圖5 IAAVS 3種工況位置跟蹤誤差

圖6給出了彈倉在空載、半載、滿載3種工作狀態下的控制輸入曲線。從圖6中可以看出,彈倉在3種工作狀態下的控制輸入曲線都很平滑,沒有出現振動現象,易于在實際實驗中實現。

空載、半載、滿載情況下的參數A隨時間的變化如圖7所示。從圖7中可以看出,在系統未受到外部擾動之前,切換函數參數A的值穩定于1,隨著外部擾動的施加,切換函數參數A的數值依據自適應律進行自適應改變,以滿足系統降低振動提高控制精度的要求;當外部擾動消失時,切換函數參數A又穩定于初始值。

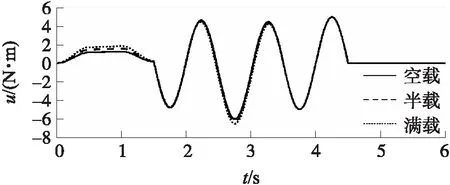
圖6 IAAVS 3種工況控制輸入

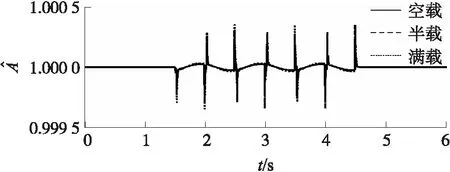
圖7 A的估計值

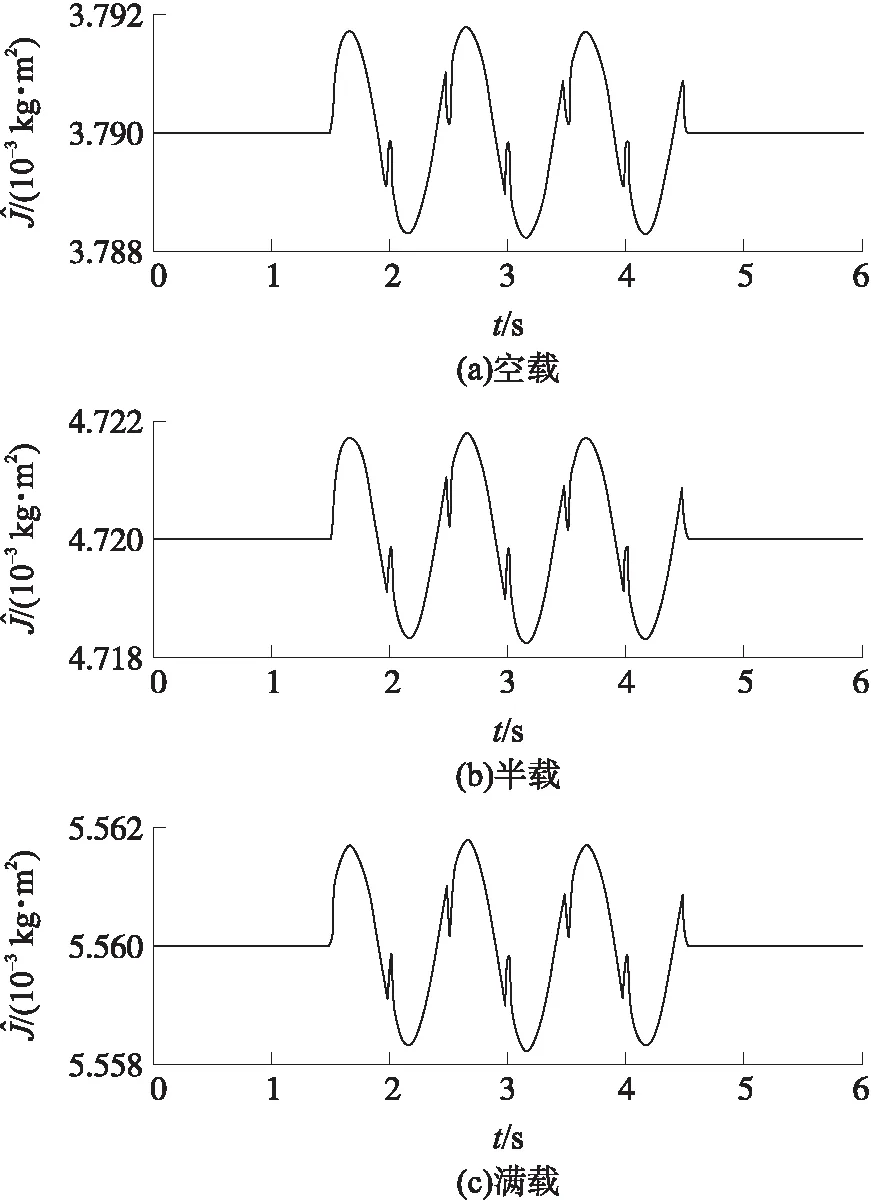
圖8 J的估計值

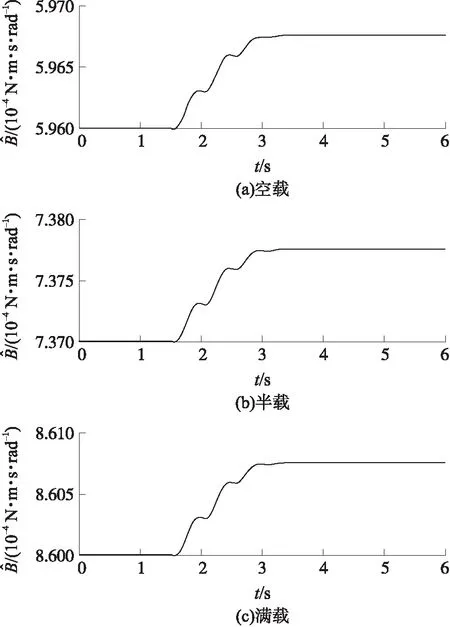
圖9 B的估計值

綜上所述,本文提出的改進自適應近似變結構控制算法,使回轉式彈倉系統具有很高的位置跟蹤精度并且能夠很好地抑制系統參數變化和外部不確定擾動對彈倉系統的影響,得出的控制力矩曲線光滑不振動,有利于在實驗中實現。

4 結論

回轉式自動化彈倉系統是一類具有系統不確定參數、等效轉動慣量以及系統等效阻尼系數都會隨著系統工作狀態發生變化的系統,同時還要考慮鏈傳動引起的多邊形效應以及系統摩擦對于位置控制精度的影響,本文主要工作包括:

①提出一種改進的自適應近似變結構控制,采用連續可導的切換控制率代替傳統不連續的控制律,在控制律中引入三角函數,使控制律變化平緩,不產生突變;

②提出對切換函數設置估計參數,使其能夠依據系統狀態進行切換函數的在線調整,采用自適應算法估計系統參數的變化,以滿足系統運動要求;

③對彈倉運動角加速度進行了優化設計,使彈倉在滿足時序要求的前提下運動更加平穩且彈倉在空載、半載、滿載條件下運動控制具有一致性。

本文對彈倉控制系統的改進,不僅有效降低了系統的振動而且明顯提高了位置控制精度。回轉式自動化彈倉在空載、半載、滿載3種工作狀態下的仿真結果表明,提出的改進自適應近似變結構控制方法具有很好的魯棒性和控制精度。