基于FLUENT的擺桿式明渠測(cè)流特性數(shù)值模擬

周義仁，石先德，張 茜

(太原理工大學(xué)水利科學(xué)與工程學(xué)院，太原 030024)

灌區(qū)精準(zhǔn)量水是提高農(nóng)業(yè)用水利用率的基礎(chǔ)所在[1]，本文針對(duì)灌區(qū)量水過(guò)程中存在的測(cè)流精度低、水頭損失大等問(wèn)題提出了一種新型量水裝置----擺桿式明渠測(cè)流裝置，其工作原理需建立擺桿擺動(dòng)角度和渠道流量之間關(guān)系進(jìn)行測(cè)流，探究該裝置在不同類型渠道和測(cè)流擺桿下的測(cè)流特性具有重要意義。隨著數(shù)值模擬技術(shù)的發(fā)展，計(jì)算流體力學(xué)所能計(jì)算的領(lǐng)域越來(lái)越多[2]，通過(guò)數(shù)值模擬方法建立數(shù)學(xué)模型解決實(shí)際工程問(wèn)題具有投入少、研究周期短、可調(diào)參數(shù)多等優(yōu)點(diǎn)。FLUENT是目前應(yīng)用最為廣泛的計(jì)算流體力學(xué)軟件，其計(jì)算方法及后處理功能十分先進(jìn)[3]。擺桿式明渠測(cè)流裝置進(jìn)行測(cè)流任務(wù)時(shí)，測(cè)流擺桿由于水流沖擊而擺動(dòng)，是屬于固體邊界在流域中產(chǎn)生的被動(dòng)運(yùn)動(dòng)，在FLUENT中，動(dòng)網(wǎng)格模型可以用來(lái)模擬由于流域邊界運(yùn)動(dòng)引起流域形狀隨時(shí)間變化的流動(dòng)情況，也可以用來(lái)模擬由于流場(chǎng)改變而導(dǎo)致固體邊界發(fā)生被動(dòng)運(yùn)動(dòng)情況[4,5]。利用FLUENT軟件對(duì)擺桿式明渠測(cè)流裝置測(cè)流特性進(jìn)行研究，可以提高該裝置的測(cè)流精度及適用性。

1 擺桿式明渠測(cè)流裝置簡(jiǎn)介

擺桿式明渠測(cè)流裝置機(jī)械結(jié)構(gòu)如圖1所示。

1-渠道邊坡；2-調(diào)平旋鈕；3-可伸縮不銹鋼支架；4-超聲波探頭；5-液晶顯示器；6-供電及數(shù)據(jù)處理模塊；7-水平儀；8-角度傳感器；9-測(cè)流擺桿圖1 擺桿式明渠測(cè)流裝置

圓柱形擺桿放置于流動(dòng)的水中時(shí)受到渠道水流阻力和升力作用，會(huì)沿水流方向擺動(dòng)，通過(guò)建立渠道流量和擺桿擺動(dòng)角度之間的關(guān)系，測(cè)得擺桿旋轉(zhuǎn)角度便可以得知渠道瞬時(shí)流量。

2 數(shù)值模擬研究

2.1 計(jì)算模型及控制方程

計(jì)算采用VOF自由液面模型，對(duì)于水氣兩相流動(dòng)，VOF模型對(duì)其進(jìn)行描述時(shí)，先定義函數(shù)qw(x,y,z,t)和qa(x,y,z,t)，它們分別表示水與空氣在某一時(shí)刻的某一單元格內(nèi)的體積分?jǐn)?shù)。而在每一個(gè)單元格內(nèi)[6]：

qw+qa=1

(1)

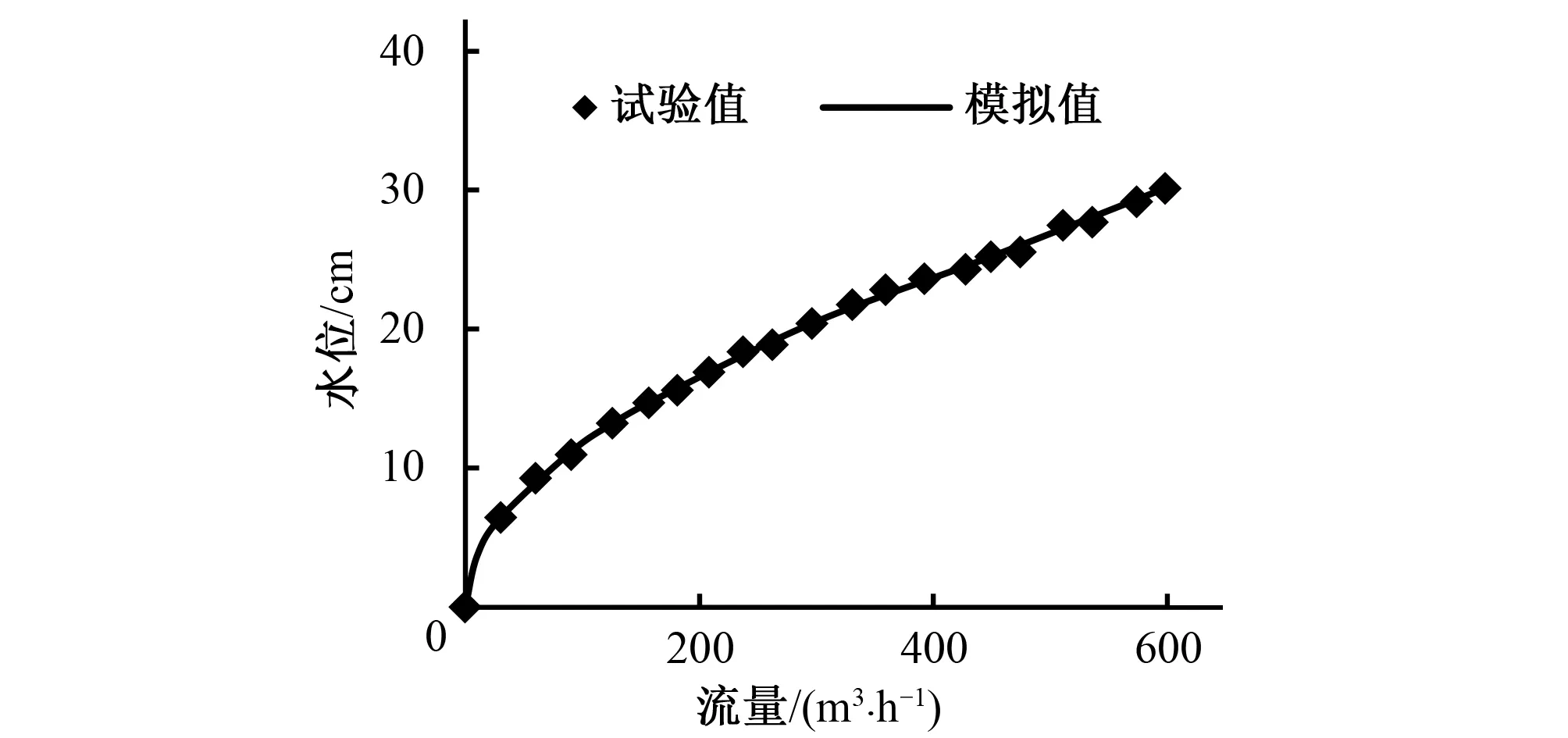
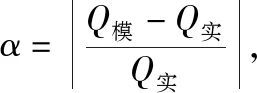
通過(guò)公式(1)能夠得到，當(dāng)qw=1時(shí)，表示在該單元格內(nèi)水的體積分?jǐn)?shù)為1，也就是這個(gè)單元內(nèi)充滿了水；反之，qa=1時(shí)，則表示這個(gè)單元內(nèi)全都是空氣；若0

(2)

式中：t為時(shí)間；ui為速度分量；xi為坐標(biāo)分量。

湍流模型選用Realizablek-ε模型，連續(xù)性方程、動(dòng)量方程、湍流動(dòng)能k方程、湍流耗散率ε方程如下所示[8]：

(3)

(4)

Gk+Gb-ρε-Ym+Sk

(5)

(6)

2.2 幾何建模及網(wǎng)格劃分

本文模擬及試驗(yàn)所用渠道為D50型U形渠道，其主要參數(shù)為：渠深0.5 m，渠道底弧半徑0.25 m，底弧圓心角163°，渠道傾角8.5°，渠頂寬度0.58 m，渠道底坡為1/1 000。為了充分模擬U形渠道水流流態(tài)并盡量減少計(jì)算機(jī)模擬時(shí)間，渠道長(zhǎng)度設(shè)為4 m，入口處1 m設(shè)置長(zhǎng)方體穩(wěn)流池，確保水流從入口處平穩(wěn)過(guò)渡到U形渠道中。設(shè)備放置于U形渠道中央，距出口2 m位置，取擺桿頂端圓心為坐標(biāo)原點(diǎn)，水流方向?yàn)閆軸正方向，豎直向上為Y軸正方向，順?biāo)鞣较蜃蟀稙閄軸正方向，如圖2所示。

圖2 坐標(biāo)軸示意圖

結(jié)構(gòu)化網(wǎng)格與非結(jié)構(gòu)化網(wǎng)格聯(lián)合進(jìn)行求解，可以很好地解決計(jì)算緩慢以及網(wǎng)格質(zhì)量差等問(wèn)題，使得模擬更加精準(zhǔn)和高效[9,10]。計(jì)算模型在最大尺度以及最小尺度之間存在較大差異(渠道長(zhǎng)達(dá)4 m，測(cè)流擺桿直徑為5 mm)，所以在擺桿上下游0.5 m以內(nèi)采用非結(jié)構(gòu)化網(wǎng)格，在擺桿運(yùn)動(dòng)范圍之外采取結(jié)構(gòu)化網(wǎng)格。設(shè)置全局網(wǎng)格最大尺寸為4 cm，在擺桿周圍進(jìn)行非結(jié)構(gòu)化網(wǎng)格劃分，并對(duì)擺桿進(jìn)行局部加密處理，擺桿表面最大網(wǎng)格尺寸為1 mm，網(wǎng)格總數(shù)約為36萬(wàn)個(gè)，網(wǎng)格劃分如圖3所示。

圖3 網(wǎng)格劃分示意圖

2.3 邊界條件及求解方法

為了更加精確的模擬渠道水流流動(dòng)對(duì)擺桿式明渠測(cè)流精度的影響，上游設(shè)置進(jìn)口為速度入口(VELOCITY-INLET)，利用平均流速來(lái)控制渠道瞬時(shí)流量大小；下游出口設(shè)置為壓力出口(PRESSURE-OUTLET)；渠道頂部設(shè)為壓力進(jìn)口(PRESSURE-INLET)，受到大氣壓強(qiáng)作用，頂部參考?jí)簭?qiáng)為101 kPa；擺桿以及渠道側(cè)面全部設(shè)為無(wú)滑移固體邊壁，渠道壁面為不銹鋼材質(zhì)，設(shè)置壁面粗糙度高度為0 cm，粗糙度常數(shù)為0.5。整個(gè)計(jì)算域中最開(kāi)始時(shí)充滿了空氣，通過(guò)VOF方法進(jìn)行迭代，自動(dòng)生成水氣交界面。

本文主要采用有限體積法進(jìn)行計(jì)算，主要步驟是進(jìn)行計(jì)算區(qū)域劃分后，進(jìn)行區(qū)域的離散化與控制方程的離散，計(jì)算區(qū)域的離散化實(shí)質(zhì)上便是上述所提到的網(wǎng)格劃分。控制方程的離散化可以利用如下所示的通用形式表示[11]：

(7)

式中：ρ為流體密度；u為液體流速；t為時(shí)間；φ為廣義變量，可以為速度、溫度或者濃度等一些待求物理量；Γ是相應(yīng)于φ的廣義擴(kuò)散項(xiàng)；Sk是廣義源項(xiàng)。

建立了可以進(jìn)行計(jì)算的代數(shù)方程組之后，需要對(duì)各個(gè)未知量的求解順序以及方式進(jìn)行特殊處理，對(duì)于瞬態(tài)計(jì)算，采用PISO算法比SIMPLE或者SIMPLEC算法更加合適。

2.4 動(dòng)網(wǎng)格設(shè)定

在FLUENT中動(dòng)網(wǎng)格更新方法主要有3種，包括彈簧近似光滑模型(Spring-based Smoothing)、動(dòng)態(tài)分層模型(Dynamic Layering)以及局部網(wǎng)格重構(gòu)模型(Local Remeshing)[12]。本文主要采用彈簧光順與局部網(wǎng)格重構(gòu)相結(jié)合進(jìn)行計(jì)算。

動(dòng)網(wǎng)格流場(chǎng)控制模型中，計(jì)算區(qū)域是變化的，其守恒方程為[13]：

(8)

FLUENT中6DOF(六自由度)模型主要是用于模擬計(jì)算域中的剛體構(gòu)件受到流體的作用之后運(yùn)動(dòng)的軌跡及狀態(tài)，通過(guò)模擬流體的運(yùn)動(dòng)對(duì)剛體產(chǎn)生的作用力，來(lái)推算剛體的運(yùn)動(dòng)軌跡。其中剛體的質(zhì)量、位移、旋轉(zhuǎn)以及轉(zhuǎn)動(dòng)慣量可以通過(guò)UDF(用戶自定義函數(shù))來(lái)進(jìn)行編寫錄入[14]。

本文主要研究3種不同材質(zhì)的測(cè)流擺桿在D50型U形渠道下的測(cè)流特性，不同材質(zhì)的擺桿參數(shù)如表1所示。

3 結(jié)果分析

3.1 水面線分析

對(duì)明渠進(jìn)行三維數(shù)值模擬時(shí)，水面線是一項(xiàng)基本研究對(duì)象，通過(guò)試驗(yàn)與模擬結(jié)果的比較，可以驗(yàn)證數(shù)值模擬的可行性。

表1 不同材質(zhì)測(cè)流擺桿參數(shù)

對(duì)不同流量下D50型U形渠道水流進(jìn)行模擬可以得到測(cè)流裝置下方(Z=0 m)水位隨流量變化圖，如圖4所示。

圖4 水位與流量關(guān)系圖

當(dāng)渠道瞬時(shí)流量為300 m3/h時(shí)，采用鋁材測(cè)流擺桿，t=0 s時(shí)開(kāi)始從入口注水，渠道水流從入口到出口水面線隨時(shí)間變化瞬態(tài)圖如圖5所示，圖中藍(lán)色區(qū)域?yàn)榭諝猓t色區(qū)域?yàn)樗鳎t藍(lán)相間區(qū)域?yàn)樗畾饨唤缑妫咨珔^(qū)域?yàn)閿[桿。觀察圖5可以發(fā)現(xiàn)，隨著入口處水流不斷涌入渠道，渠道中水位逐漸上升，當(dāng)t=6.87 s以后，水位趨于平緩。穩(wěn)流池與渠道相接處水面略有壅高，這是由于穩(wěn)流池出口截面較小，水流撞擊壁面后造成水位上升。測(cè)流設(shè)備上下游1 m水流平緩，在渠道出口處水位有所下降。由圖4與圖5可以發(fā)現(xiàn)，利用數(shù)值模擬對(duì)U形渠道進(jìn)行仿真模擬得到的渠道水位與試驗(yàn)結(jié)果相近，所以利用VOF方法以及Realizablek-ε湍流模型對(duì)渠道水流進(jìn)行數(shù)值模擬可以得到與實(shí)際相符的結(jié)果。

圖5 300 m3/h流量下渠道沿程水面線變化圖

3.2 流速分布

為了解U形渠道過(guò)水?dāng)嗝媪魉僮兓卣鳎瑢?duì)測(cè)流設(shè)備下方(Z=0 m)測(cè)流斷面進(jìn)行流速分析，如圖6所示為不同流量下，渠道過(guò)水?dāng)嗝嫜厮鞣较?Z軸正方向)水流流速分布云圖。

由圖6可以發(fā)現(xiàn)，在底坡為1/1 000的D50型U形渠道中，隨著渠道內(nèi)流量的增加，過(guò)水?dāng)嗝婷娣e增大，水位逐漸升高，水流流速逐漸增大，當(dāng)流量為150 m3/h時(shí)，最大流速為0.96 m/s，當(dāng)流量為600 m3/h時(shí)，最大流速達(dá)到1.37 m/s。對(duì)于渠道斷面沿水流方向的流速分布而言，在靠近渠道邊壁的流速急劇下降，在渠道邊壁區(qū)域接近于0 m/s，其最大流速位于水面下方，在氣液交界面處，流速較緩，這與渠道實(shí)際流速分布規(guī)律相吻合。

3.3 動(dòng)網(wǎng)格變化分析

對(duì)于動(dòng)網(wǎng)格的計(jì)算方法，本文主要采用彈簧光順與局部網(wǎng)格重構(gòu)相結(jié)合進(jìn)行計(jì)算。彈簧光順將網(wǎng)格節(jié)點(diǎn)視為可變形的彈簧，固體邊界發(fā)生位置變化時(shí)，將會(huì)擠壓或者拉伸網(wǎng)格，通過(guò)求解彈簧的應(yīng)力平衡方程得到新網(wǎng)格的節(jié)點(diǎn)位置，但是其只能處理網(wǎng)格微小變形的情況，當(dāng)網(wǎng)格變形較大時(shí)，則需要利用局部網(wǎng)格重構(gòu)技術(shù)。針對(duì)網(wǎng)格尺寸以及畸變率，當(dāng)網(wǎng)格出現(xiàn)較大程度的變形時(shí)，將會(huì)對(duì)該區(qū)域的網(wǎng)格進(jìn)行網(wǎng)格重構(gòu)，通過(guò)守恒定律以及插值映射從舊網(wǎng)格中得到物理量的大小。如圖7所示，以不銹鋼材質(zhì)擺桿在不同流量的水流作用下產(chǎn)生網(wǎng)格重構(gòu)的變化為例，對(duì)動(dòng)網(wǎng)格變化進(jìn)行分析。圖7藍(lán)色區(qū)域?yàn)榭諝猓t色區(qū)域?yàn)樗鳎t藍(lán)相間區(qū)域?yàn)樗畾饨唤缑妗?/p>

圖6 不同流量下斷面流速分布云圖

圖7 不銹鋼材質(zhì)擺桿局部網(wǎng)格變化

由圖7可以發(fā)現(xiàn)，當(dāng)擺桿受到水流作用向下游擺動(dòng)時(shí)，擺桿周圍的網(wǎng)格發(fā)生變形，下游網(wǎng)格受到擺桿擠壓，體積變小，而擺桿上游位置的網(wǎng)格體積增大。隨著流量的增大，擺桿擺動(dòng)的角度隨之增大，動(dòng)網(wǎng)格更新的區(qū)域也隨之增大，且之前擺桿經(jīng)過(guò)的區(qū)域網(wǎng)格變得更加密集。在整個(gè)迭代計(jì)算過(guò)程中，網(wǎng)格體積始終沒(méi)有出現(xiàn)負(fù)體積。通過(guò)模擬研究發(fā)現(xiàn)，鋁材以及有機(jī)玻璃兩種材質(zhì)的測(cè)流擺桿與圖7中不銹鋼材質(zhì)擺桿周圍網(wǎng)格變化規(guī)律相似，說(shuō)明采用FLUENT中6DOF動(dòng)網(wǎng)格模型模擬擺桿式測(cè)流裝置測(cè)流特性是可行的。

3.4 測(cè)流公式及精度分析

擺桿式明渠測(cè)流裝置測(cè)得流量Q與以下因素有關(guān)：水的密度 、重力加速度g、測(cè)流擺桿密度 、測(cè)流擺桿長(zhǎng)度L、測(cè)流擺桿直徑D、測(cè)流擺桿被水推動(dòng)的水平位移d(d=Lsinθ)、水中泥沙濃度S、水動(dòng)力黏滯系數(shù)v、渠道糙率n以及渠道底坡i。擺桿式明渠測(cè)流裝置的測(cè)流計(jì)算公式可以通過(guò)量綱分析法推導(dǎo)得到。選取d，g，ρ桿3個(gè)相互獨(dú)立的量作為研究基本物理量，最終可以得到以下測(cè)流公式：

(9)

(10)

Q=Ksin2.5θ

(11)

對(duì)D50型U形渠道下不同材質(zhì)的測(cè)流擺桿測(cè)流特性進(jìn)行數(shù)值模擬，得到3種材質(zhì)擺桿在不同流量下相應(yīng)擺動(dòng)角度，利用線性擬合得到式(11)中系數(shù)K的大小，便得到了擺桿式明渠測(cè)流裝置在該渠道下的測(cè)流公式，如表2所示。

表2 不同材質(zhì)測(cè)流擺桿測(cè)流公式

圖8為模擬值與試驗(yàn)值對(duì)比圖，主坐標(biāo)軸反映了不同材質(zhì)的測(cè)流擺桿sin2.5θ與渠道流量Q之間的關(guān)系，次坐標(biāo)軸反映了利用表2算得流量與實(shí)際流量之間的相對(duì)誤差。由圖8可以發(fā)現(xiàn)，不同材質(zhì)的測(cè)流擺桿在U形渠道下，渠道流量Q與擺桿擺動(dòng)角度sin2.5θ之間成正比例函數(shù)關(guān)系，模擬值與試驗(yàn)值變化一致。利用測(cè)流公式得到渠道流量與真實(shí)流量之間相對(duì)誤差α較小，其中不銹鋼材質(zhì)的測(cè)流擺桿測(cè)得流量最大相對(duì)誤差為5.33%，平均相對(duì)誤差為2.5%；鋁材測(cè)流擺桿測(cè)得流量最大相對(duì)誤差為5.55%，平均相對(duì)誤差為1.87%；有機(jī)玻璃材質(zhì)測(cè)流擺桿測(cè)得流量最大相對(duì)誤差為5.26%，平均相對(duì)誤差為2.22%。

4 結(jié) 語(yǔ)

利用FLUENT對(duì)擺桿式明渠測(cè)流裝置在底坡為1/1 000的D50型U形渠道下測(cè)流特性進(jìn)行數(shù)值模擬研究，通過(guò)數(shù)值模擬以及試驗(yàn)數(shù)據(jù)對(duì)比分析得到以下結(jié)論。

圖8 不同材質(zhì)擺桿流量與角度關(guān)系圖

(1)利用FLUENT中VOF模型與Realizablek-ε湍流模型對(duì)D50型U形渠道下水流特性進(jìn)行模擬研究是可行的，模擬渠道沿程水面線與試驗(yàn)相符。渠道過(guò)水?dāng)嗝嫔狭魉俜植家?guī)律為：在靠近渠道邊壁的區(qū)域水流流速急劇下降，在邊壁旁趨近于零，而水流最大流速并不是位于水面位置，而是在水面下方的位置，這也與國(guó)內(nèi)外其他學(xué)者研究結(jié)論一致。

(2)利用6DOF動(dòng)網(wǎng)格模型對(duì)測(cè)流擺桿擺動(dòng)特性進(jìn)行模擬是可行的，通過(guò)水流與擺桿之間的耦合計(jì)算可以得到擺桿的擺動(dòng)角度與渠道流量大小之間的變化規(guī)律，隨著渠道內(nèi)瞬時(shí)流量的增大，擺桿擺動(dòng)的角度也逐漸增大，擺桿周圍非結(jié)構(gòu)化網(wǎng)格產(chǎn)生重構(gòu)。

(3)利用數(shù)值模擬對(duì)擺桿式測(cè)流裝置測(cè)流精度進(jìn)行研究，發(fā)現(xiàn)量綱分析得到的測(cè)流公式Q=Ksin2.5θ中系數(shù)K大小隨著擺桿密度的減小而減小，測(cè)得流量與實(shí)際流量之間平均相對(duì)誤差小于3%，可以滿足明渠測(cè)流精度要求。

本文對(duì)擺桿式明渠測(cè)流裝置測(cè)流特性進(jìn)行數(shù)值模擬研究，模擬結(jié)果與實(shí)際情況一致，充分驗(yàn)證了該測(cè)流裝置的可行性，對(duì)提高該裝置測(cè)流精度有重要意義，為灌區(qū)精準(zhǔn)量水的發(fā)展提供了新思路。