基于MATLAB的非線性電路特性仿真研究

李佳倫

【摘 要】實際電路都是非線性的。非線性電路具有很多和線性電路完全不同的特性，表現出非線性電路獨有的一些行為。論文利用MATLAB搭建了不同的非線性電路模型，然后利用數值仿真，分析了非線性電路穩態不唯一、極限環、混沌等三個典型特性，直觀展現了非線性電路中穩定與不穩定平衡點、極限環、混沌等不同行為的具體表現，分析了非線性電路軌跡與初始點的相關性，為了解非線性電路特殊的行為提供參考。

【關鍵詞】非線性電路;平衡點;極限環;混沌

中圖分類號： TN710 文獻標識碼： A 文章編號： 2095-2457（2019）24-0047-004

DOI：10.19694/j.cnki.issn2095-2457.2019.24.023

【Abstract】All actual circuits are nonlinear. Nonlinear circuits have many different characteristics from linear circuits， and some special behaviors would appear. The paper uses MATLAB to build different nonlinear circuit models， and then uses numerical simulation to analyze three typical characteristics of nonlinear circuits， i.e. multiple steady states， limit cycle and chaos， and visually shows the stable equilibrium point and unstable equilibrium point， limit cycle， chaos and other characteristics in nonlinear circuits. The paper also analyzes the dependence of trajectories of nonlinear circuits on the initial points. The results provide a reference for understanding the special behaviors of nonlinear circuits.

【Key words】Non-linear circuit; Equilibrium point; Limit cycle; Chaos

0 引言

在線性電路中，線性元件的特點是其參數不隨電壓或電流而變化。若元件的參數隨著電壓或電流而變化，則該元件稱為非線性元件，含有非線性元件的電路稱為非線性電路。嚴格來說，一切實際電路都為非線性電路，因為實際元件的參數總會隨著電壓或者電流變化而發生改變。一般情況下，把非線性程度比較微弱的電路元件作為線性元件來處理，不會有太大影響，并且還能夠簡化運算。但是，很多非線性元件的非線性特征不容忽略，若將這些元件按照線性元件來處理，計算結果必會與實際測量值相差甚遠，無法解釋電路中的某些現象。因此分析研究非線性電路具有重要意義。

和線性電路相比，非線性電路的特性要復雜得多，會出現大量獨特的現象，如穩態不唯一、極限環、混沌等[1-4]。但是，目前對于一般非線性電路的還缺乏有效的解析分析方法，因此，本文主要采用數值仿真方法對非線性電路的特性進行研究。

1 穩態不唯一

電路的穩態解可通過求解表征電路平衡狀態的一組代數方程組獲得。對于線性電路，該代數方程是線性的，解是唯一的，因此線性電路的穩態唯一。對于非線性電路，該代數方程是非線性方程，可能存在多解，導致非線性電路的穩態不唯一。

當給非線性電路一個直流電源激勵時，若電流和電壓不再隨時間變化，則此時的電路處于平衡狀態。若這時給電路一個微小的擾動并消除，使電壓電流略微偏離穩態。如果電壓電流能變回原來的狀態，則稱這個平衡點是穩定的，反之，則此平衡點是不穩定。

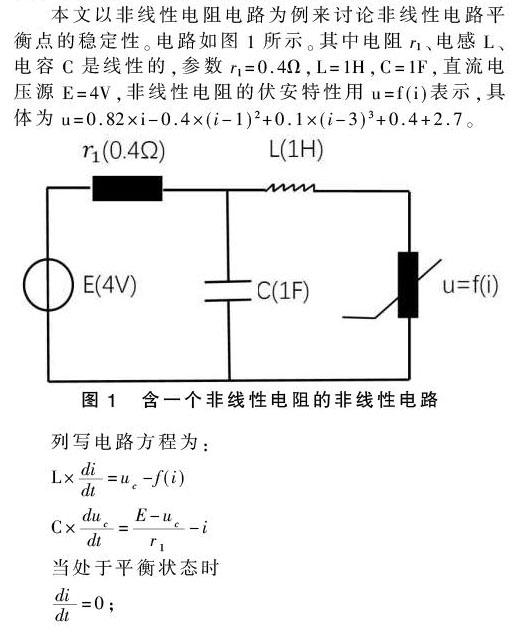
本文以非線性電阻電路為例來討論非線性電路平衡點的穩定性。電路如圖1所示。其中電阻r1、電感L、電容C是線性的，參數r1=0.4Ω，L=1H，C=1F，直流電壓源E=4V，非線性電阻的伏安特性用u=f（i）表示，具體為u=0.82×i-0.4×（i-1）2+0.1×（i-3）3+0.4+2.7。

在圖2的3個平衡點中，有穩定的和不穩定的。給電路設定一系列初始值，用MATLAB進行仿真，觀察在u-i平面上的軌跡，經過一段時間后會收斂到哪個點。結果圖如3所示。可以直觀地看見，電路最后到達的穩態在A、C兩點，而B點為不穩定點，一系列初始值都不會收斂于B點。非線性電路有多個平衡點，電路收斂于哪個平衡點由起始條件決定。

2 極限環

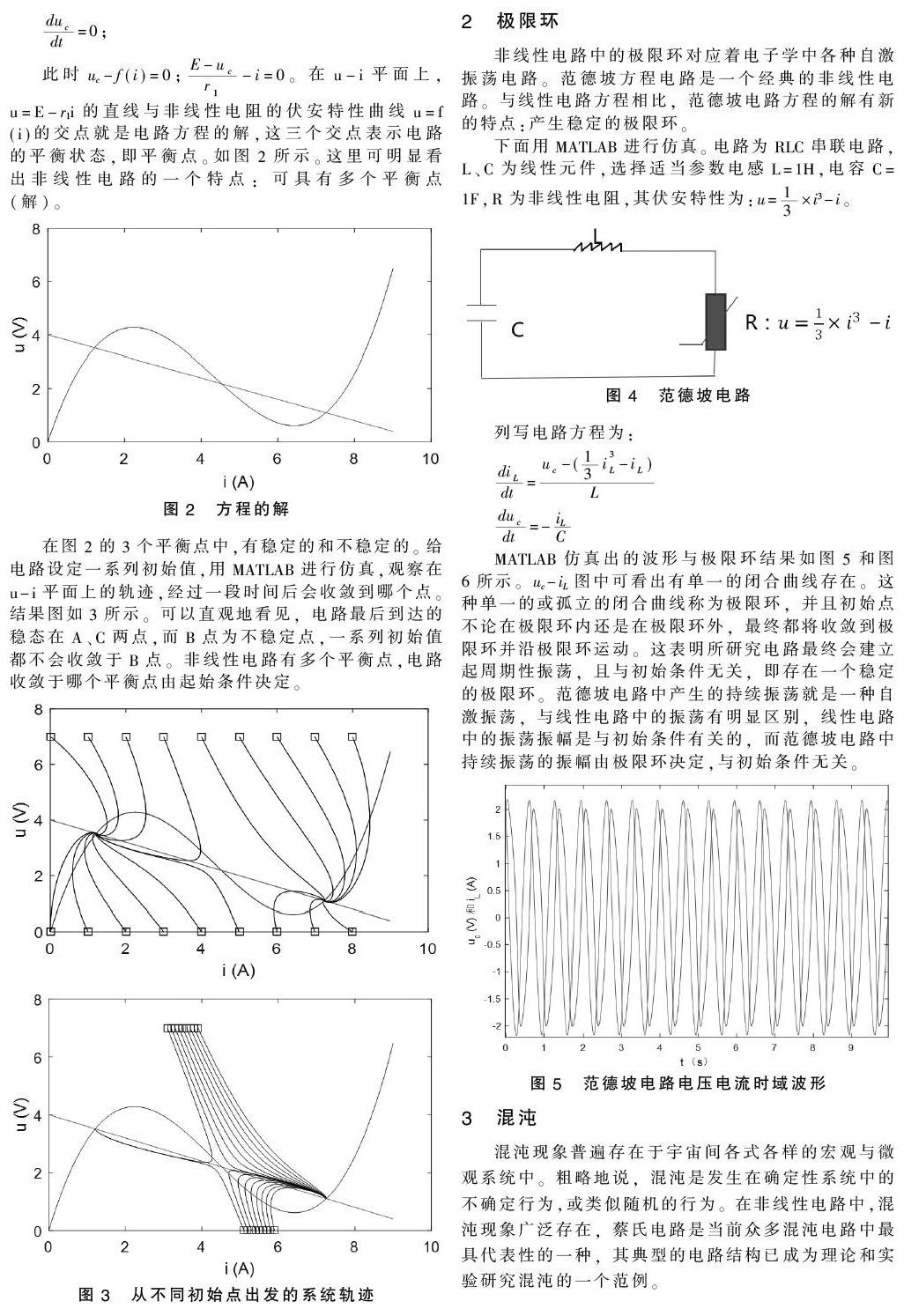
非線性電路中的極限環對應著電子學中各種自激振蕩電路。范德坡方程電路是一個經典的非線性電路。與線性電路方程相比，范德坡電路方程的解有新的特點：產生穩定的極限環。

MATLAB仿真出的波形與極限環結果如圖5和圖6所示。uc-iL圖中可看出有單一的閉合曲線存在。這種單一的或孤立的閉合曲線稱為極限環，并且初始點不論在極限環內還是在極限環外，最終都將收斂到極限環并沿極限環運動。這表明所研究電路最終會建立起周期性振蕩，且與初始條件無關，即存在一個穩定的極限環。范德坡電路中產生的持續振蕩就是一種自激振蕩，與線性電路中的振蕩有明顯區別，線性電路中的振蕩振幅是與初始條件有關的，而范德坡電路中持續振蕩的振幅由極限環決定，與初始條件無關。

3 混沌

混沌現象普遍存在于宇宙間各式各樣的宏觀與微觀系統中。粗略地說，混沌是發生在確定性系統中的不確定行為，或類似隨機的行為。在非線性電路中，混沌現象廣泛存在，蔡氏電路是當前眾多混沌電路中最具代表性的一種，其典型的電路結構已成為理論和實驗研究混沌的一個范例。

蔡氏電路[5]是蔡少棠教授首次發表出的，它是能產生混沌行為最簡單的自治電路，僅包含三個儲能元件，以及一個特性相對簡單的非線性電阻。蔡氏混沌系統是由線性電阻、電感、電容和一個非線性，電阻原件組成，它滿足混沌電路產生的條件為：

（1）一個或者多個的非線性元件。

（2）一個或者多個的本地有源電阻。

（3）三個或者更多個能量存儲元件。

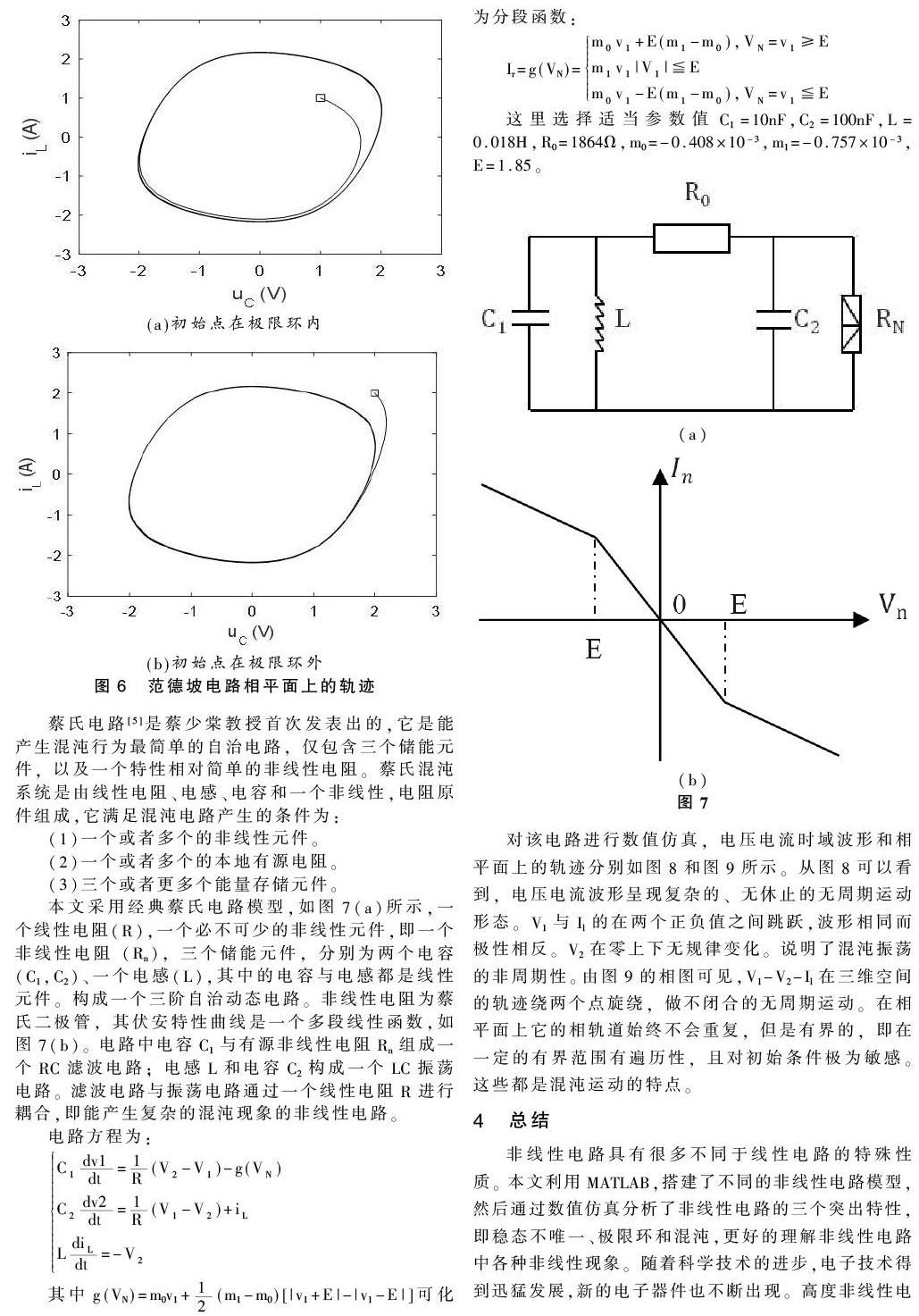
本文采用經典蔡氏電路模型，如圖7（a）所示，一個線性電阻（R），一個必不可少的非線性元件，即一個非線性電阻（Rn），三個儲能元件，分別為兩個電容（C1，C2）、一個電感（L），其中的電容與電感都是線性元件。構成一個三階自治動態電路。非線性電阻為蔡氏二極管，其伏安特性曲線是一個多段線性函數，如圖7（b）。電路中電容C1與有源非線性電阻Rn組成一個RC濾波電路;電感L和電容C2構成一個LC振蕩電路。濾波電路與振蕩電路通過一個線性電阻R進行耦合，即能產生復雜的混沌現象的非線性電路。

對該電路進行數值仿真，電壓電流時域波形和相平面上的軌跡分別如圖8和圖9所示。從圖8可以看到，電壓電流波形呈現復雜的、無休止的無周期運動形態。V1與Il的在兩個正負值之間跳躍，波形相同而極性相反。V2在零上下無規律變化。說明了混沌振蕩的非周期性。由圖9的相圖可見，V1-V2-Il在三維空間的軌跡繞兩個點旋繞，做不閉合的無周期運動。在相平面上它的相軌道始終不會重復，但是有界的，即在一定的有界范圍有遍歷性，且對初始條件極為敏感。這些都是混沌運動的特點。

4 總結

非線性電路具有很多不同于線性電路的特殊性質。本文利用MATLAB，搭建了不同的非線性電路模型，然后通過數值仿真分析了非線性電路的三個突出特性，即穩態不唯一、極限環和混沌，更好的理解非線性電路中各種非線性現象。隨著科學技術的進步，電子技術得到迅猛發展，新的電子器件也不斷出現。高度非線性電子器件的廣泛應用，使得研究非線性電路十分必要。

【參考文獻】

[1]徐清華.非線性電路分析[M].高等教育出版社，1992.

[2]劉崇新.非線性電路理論及應用[M].西安交通大學出版社，2007.

[3]張新國等編著.非線性電路：基礎分析與設計[M].高等教育出版社，2011.

[4]邱關源，羅先覺主編.電路.第5版[M].北京：高等教育出版社，2006.

[5]趙桂清.蔡氏混沌電路分析研究[J].科技創新與應用， 2015（26）.