圖像復原用的一種改進的最大熵法

文/王吉會

1 圖象退化模型

所研究的圖象復原是圖1的模型為基礎的。

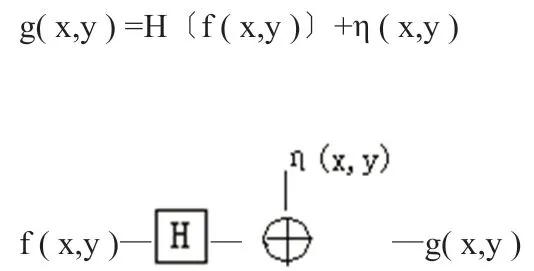
當H為一線性算子時，有：

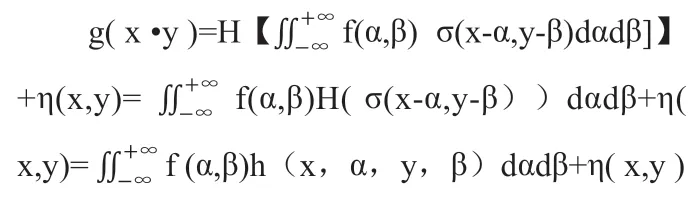
其 中：h(x,α,y,β)=H〔δ (x —α，y—β)〕當h(x,α,y,β)是位置不變的時，則：

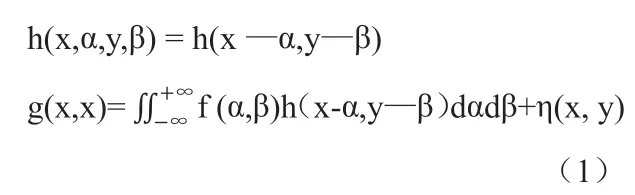
為了方便清楚明了，將二維圖象分解為一維序列。這樣（1）式可以表示為：

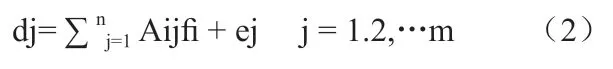
其中：{ej}是均值為零的白噪聲。 {fi}為原始圖象。

{dj}污染后的圖象。{Aij}是傳遞函數。

2 傳統最大熵復原法

2.1 圖像的熵

圖像的熵是一種圖像信息量的表示方法，代表了圖像的平均信息量。離散分布（3）的熵為：

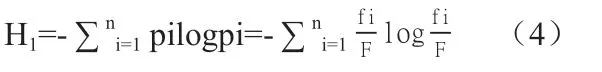
當F=常數時，則H1=max與H= —Σfilogfi = max一致，因為H= max，必然有H1=max。故令熵的

另外還有一種Burg熵，因其使用的狹隘性，本文就不在此贅述了。

2.2 傳統的最大熵復原方法

傳統的最大熵復原方法主要是從頻譜關系考慮和利用最大熵法復原。

設Sg(U，v),Sf(u,v)，Sη(u,v)分別代表模糊圖象、原圖象、噪聲的功率譜密度.

則它們有：

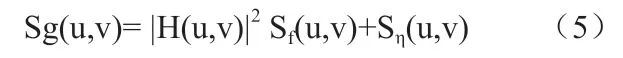
現在，我們要尋找一個譜均衡器P(u,v)，使g(x,y)通過它時，能得到輸出Sf(u，v)

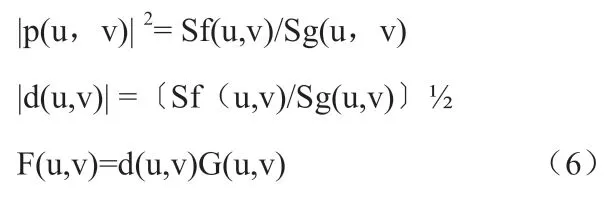
不難看出，（6）式中要用到g(x，y）的功率譜，估計Sg(u,v)時，可以利用最大熵法。

第二：從時域，利用優化方法來求。

值問題3再利用#優法求極值，得出最大熵法情況下的復原圖象。

以上兩種方法均有缺點。第一種方法Sf(u,v)較難求。第二種方法尋優困難。用最速下降法尋優，其步長又難以選擇。用共扼方向法尋優，復雜度高。用近視法，則降低了精度。

3 改進的最大熵法

3.1 最大熵復原應滿足的約束條件

而且，fi＞0 i=1、2、…、n

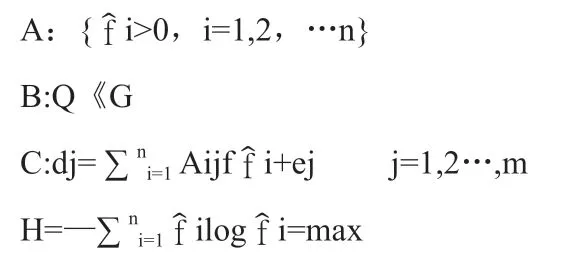
椐拉格朗日乘子法，我們建立目標函數為：

其中：λ為拉格朗日除子。

下面我們求目標函數的極大值。

令：J=max,則需使：J’=0 所以‘有

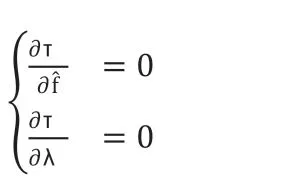
如式（8）（9）（10）（11）所示。

滿足（10），（11）的f即是J的駐點，是候選的最大值點。

3.2 J的凹凸性證明

定理：當入＞0時，J是嚴格上的凸函數。據上述定理，當入＞0時，滿足（10），（11）的f就是J最大值點，即我們要得的復原圖象。

3.3 遞推公式

因為當η很大時，我們不能直接由（10），（11）解出f,所以，要通過別的途徑。在此我們利用遞推法。將（10）式兩邊求引，并賦以遞推序號，得：如式（12）所示。

由（12）得遞推公式為：

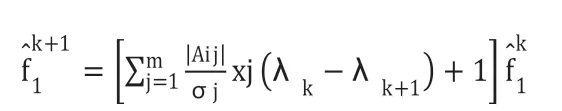
綜上，遞推求f時應先按（13），后按（11）式求。即滿足：

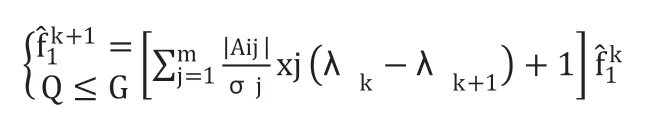
3.4 初值

令入=0，由（10）得出f的初值為=e-1，i=1、2、…n

用此數值作為迭代初值復原出來的圖象精度高。而任選一初值，則或者迭代后產生的圖象精度太低，或者得出負圖像，等等。

3.5 算法的收斂性

圖1

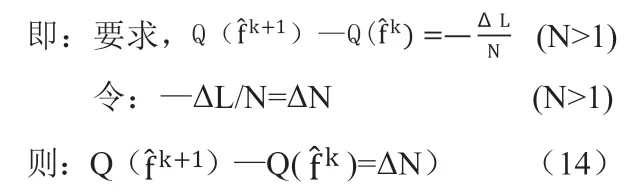
據泰勒公式，有：如式（15）所示。

上式兩邊分別轉置，得：

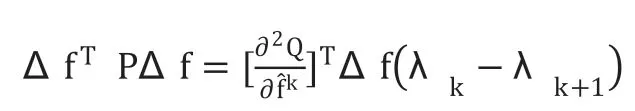
代入（15），得：

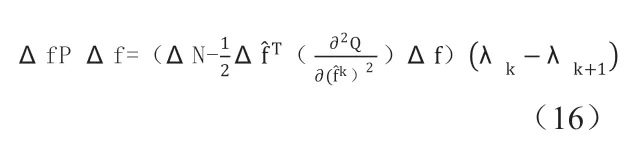
令：x1=ΔfTPΔf

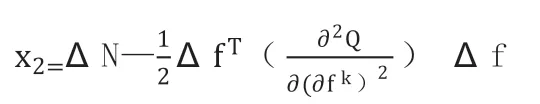
則可知，X1＞0，當ΔL＞0,ΔN＜0,∴x2＜0

因此，這時（16）式成為：

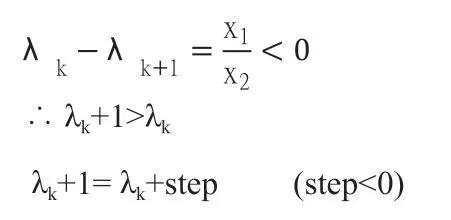
綜上，當Q（fk）＞G時（這時ΔL＞o),下一步要求λk + 1比λk大，才能保證,Q(fk+1）比Q（fk）更接近于門限值G。而Q(f°)＞G,(因為fi≤1),所以此算法收斂。因此，我們得到結論： 若我們選擇門限值m1＜G＜m2，按（11），（13）式我們一定可得到復原圖象。其中：mi =m- m /10。 m2==m + m/10,這是我們實驗中得到的。mi,m2不能選得間隔太大或太小。如果太大，則復原精度低；而太小，則復原速度慢。

4 算法與結論

根據以上理論指導，我們編寫了相應的程序，進行了實驗。通過實驗我們得知，“改進的最大熵法”比傳統的最大化熵法復原速度快，精度高。

5 實驗結果

實驗結果如照片如圖1所示。