求解靜態流水車間調度的改進遺傳算法
文/顧蕾
1 引言
目前,制造業雖然發展快速,但是很多制造業企業的生產車間還是在使用以人的經驗為主的生產調度方式。生產一線工人主要依靠自己日積月累的經驗來進度產品生產的調度,在這種模式下很難實現生產的標準化,很容易產生生產設備使用不均衡、浪費時間等問題。這一系列文體的產生無形之中推動了生產方式的創新,科學合理的基于人工智能化的生產調度方式由此產生。靜態流水車間是在開始調度之前全部工件就已經做好即將加工的準備,假設不會發生突發故障,開始加工后工件像流水一樣流入流出。在這種車間模式下所有的工件加工步驟都是一樣的。
Johnson[1]最先解決了兩臺機床的flowshop調度問題,從此專家學者么開始了對于不同類型車間的調度問題的研究。在此之前的生產調度問題的解決全是依靠工人們積累的經驗來解決的,后來人們開始使用運籌學、線性規劃、拉格朗日松弛、分支定界法等應用數學的方法來解決生產調度問題。再后來人們開始引入算法,依靠智能算法去解決生產中的調度問題,例如啟發式算法,Rajendran和Ziegler[2],Wang等[3]就依靠啟發式算法解決了某些類型車間的調度問題。當前情況下,相對來說由Framinan和Leiste[4]給出的一種構造型啟發式算法,算是最優的啟發式算法。最近時間,人們對于遺傳算法的研究越來越深入,更多的學者開始選擇使用遺傳算法來解決各種類型車間的調度問題[5-7]。但是標準的遺傳算法本身就存在一定的缺陷,例如容易出現早熟或者容易陷入局部最優。這些缺點如果在算法實際執行之前不解決的化,就會帶入到實際的應用當中,那么我們得出的所謂的最優解很有可能并不是最優解。本文針對GA的這些缺陷,對標準GA進行交叉和變異上的改進,提出一種改進遺傳算法對靜態流水車間進行求解,并驗證改進后的結果更優。
2 問題描述
靜態流水車間調度問題研究就是在調度之前就做好準備的n個工件逐個流入m臺機器中(假設機器不會發生故障),工件排成一隊在m臺機器上一次性流過,一臺機器一次只能加工一個工件,每個步驟的準備時間和加工時間已知,求解此類型車間最優的調度方案。
3 求解靜態流水車間調度的改進GA算法
3.1 求解思想
當要解決實際生產當中的問題的時候,選取的算法的效率是否能滿足需求是解決問題的關鍵。首先要做的就是選取具體的參數合集,然后通過使用GA算法去尋找此參數合集當中的最優解。我們在選取參數的時候主要關注群體的規模、交叉率和變異率這幾項指標。當我們選取求解的參數不同時,GA算法的性能也會受到不同的影響,求解的結果也會不相同。綜上所述,要想體現GA算法的最優性能,最先要做的就是選取合適的參數集。
當通過算法去進行問題的優化的過程中,如何去選擇合適的Pc和Pm,這是是需要不斷地試驗反復的嘗試才能夠確認的,這是一個相當復雜繁瑣的過程,需要不斷地嘗試,嘗試過后確定最佳的Pc和Pm。
在改進的CA算法中,要求Pc和Pm的值不是固定的,而是要隨著個體適應度的變化二變化的。當種群在進行搜索的時候出現個體適應度越來越靠近或出現局部最優的時候,Pc和Pm的值會自動增加,使種群的適應度趨于分散然后跳出局部最優的困境。當種群在進行搜索的時候出現個體適應度越來越分散的時候,Pc和Pm的值會反方向變動,通過減小概率來保證優良的個體能夠不被淘汰。在交叉和變異的過程中,如果個體適應度高于群體平均水平,Pc和Pm的值自動降低,保證此個體能維持高適應度然后進入到下一代;如果個體適應度低于群體平均水平, Pc和Pm的值自動升高,使該個體在交叉或者變異的過程中被淘汰[8]。所以Pc和Pm在改進后的GA算法當中并不是固定的數值,而是隨著適應度的變化而改變的。
3.2 求解步驟
3.2.1 編碼
該編碼方式選取以工件在機器上的加工順序來進行編碼,即n道工序的編碼長度就為n,基因數為n-1,以10道工序編碼為例,隨機產生一組編碼:σ7,σ6,σ8,σ10,σ9,σ4,σ3,σ5,σ2,σ1,該編碼用集合來表示:
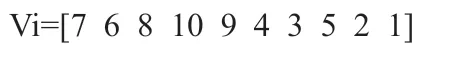
T(ji,k)表示工件σi在機器k上的加工所需時間, n個工件在m臺機器上的加工所需要的時間為:
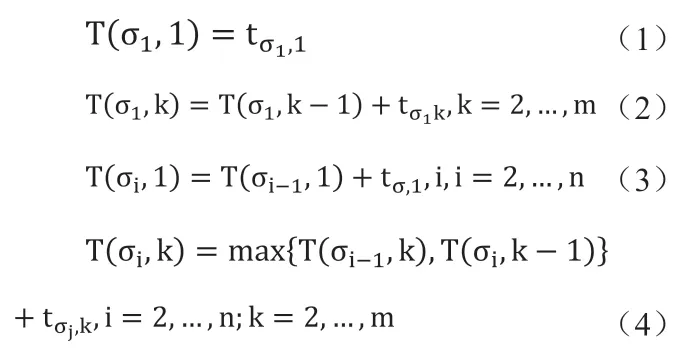
最大完成時間為:

求的是{σ1,σ2,…,σn},使得Tmax的值最小,即求最小化最大完成時間。
3.2.2 生成初始種群
隨機生成初始種群,然后取適應度高的個體,把它們放入隨機種群當中,然后在隨機產生個體,如此反復進行下去,直到達到需要的種群數后跳出循環。
3.2.3 個體適應度函數
求解的目標函數為適應度函數,Ckmax為最大完成時間函數,表示第k個染色體的最大加工完成時間。用此公式來計算單個染色體的適應度。適應度函數為:
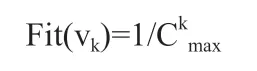
3.2.4 GA算子的設計
(1)選擇。錦標賽選擇法:
每一輪里選擇一個選項后,在之前的選擇中再進行選擇。通常最后的選擇就是錦標賽的“獲勝者”。選取n個個體,個體i的適應度用Fi表示,此時個體i可能被選中遺傳到下一代的概率為:
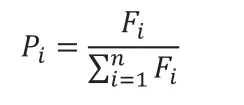
(2)交叉。
1.隨機選擇父本個體兩個;
2.隨機生成兩個自然數r1和r2,r1<r2;
3.將r1至r2之間的片段互換位置,得到兩個新的子代,然后得到的兩個子代進行修補,使其存在沖突
例如:取父本基因片段為[d,c,a,b,e][e,c,b,d,a];r1=2,r2=4;
進行交叉得到:[a,c,b,d,e][e,c,a,b,a];
進行修補后得到:[a,c,b,d,e][e,c,a,b,d];
(3)變異。
1.隨機選擇父本個體兩個r1,r2
[a,c,b,d,e][e,c,a,b,d];
2.逆轉變異
隨機從染色體中截一段基因,接著把該片段反序置換,然后插回斷裂處。
例如:r1=2,r2=4;那么染色體的變異為[a,d,b,c,e][e,b,a,c,d]
3.3 算法實現
采用國際標準算例15×15來進行標準GA算法和改進GA算法的比較。
3.3.1 標準GA算法
例:種群數M=100,迭代次數T=150,代溝GGAP=1,交叉率Pc=0.3,變異率Pm=0.2;工件數n=15,工序數m=15。
3.3.2 改進GA算法
例:種群數M=100,迭代次數T=150,代溝GGAP=1,交叉率Pc1=0.3,Pc2=0.5;變異率Pm1=0.1,Pm2=0.3;工件數n=15,工序數m=15。
3.4 結果比較
3.4.1 最優工序發生變化
標準遺傳算法:
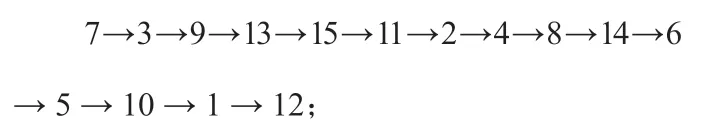
改進遺傳算法:
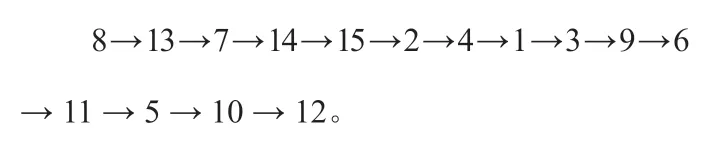
3.4.2 最小最大時間改變
根據結果可知在40代時就已經取得了最優,出現早熟現象,對標準遺傳算法進行改進從迭代曲線可以看出標準遺傳算法在迭代到40代的時候就達到了最優,出現過早收斂現象,而改進后的迭代結果現實在60代以后才開始出現收斂,同時求解最小最大完成時間得出后者時間更短。
4 結論
本文從靜態流水車間著手解決其調度問題,采用GA算法求解后發現出現早市現象,于是進行算法改進,引入可自我調節的交叉率和變異率,改進后的GA算法,經過標準算例認證,明顯優于標準GA算法得出的結果,改進后的GA算法解決了標準GA算法出現過早收斂的問題,從而達到要求的優化效果,對于靜態流水車間的調度優化提供了更多一種方法。

