一種基于改進置信度傳播的個性化推薦算法?
龔 安 孫育紅
(中國石油大學(華東)計算機與通信工程學院 青島 266580)
1 引言
隨著電子商務的廣泛普及,推薦系統獲得了極大的發展并且已經應用于生活的方方面面。推薦算法是推薦系統的核心,目前常用的推薦算法有協同過濾推薦[1]、基于知識的推薦[2]、基于內容的推薦[3]、基于圖模型的推薦[4]及混合推薦[5]等。這些推薦算法通過預測用戶對項目的評分來推薦項目給用戶并且已經在各自相應的文獻中證明了其有效性。然而在某些情況下,比如在為顧客推薦商品時,應該挑選出特定數量的商品并將其排列順序給顧客,尤其在網上購物時,一個包含特定數量商品的排名列表更受顧客歡迎。這類情況下,項目的排名被認為要比預測用戶對項目的評分更重要。因此研究找到排名前n位的項目推薦即TOP-N推薦[6~7]而不是單純預測用戶對項目的評分是很有必要的。
基于RWR的方法[8~9]就是一種TOP-N推薦,它將概率統計模型中的隨機游走算法引入到個性化推薦中,通過計算項目集和用戶集的用戶-項目排序矩陣來計算用戶對項目的偏好程度,在評估排名結果度量上明顯要優于傳統的協同過濾算法。文獻[10]在隨機游走算法的基礎上進行了改進優化,提出了一種基于項目-標簽導向的隨機游走推薦模型,在一定程度上消減了數據稀疏性問題和冷啟動問題。文獻[11~12]也對該算法進行了不同的改進優化,有效地提高了精確度和項目的多樣性。然而,上述算法都只考慮了馬爾科夫場中均勻的結點卻未考慮異相的結點,一定程度上影響了推薦結果的精度,并且這些算法在矩陣分解時消耗的空間代價極大。
針對上述問題,將置信度傳播算法(Belief Propagation,BP)[13]引入到推薦系統中隱式地挖掘用戶對項目的偏好,BP算法利用信息在馬爾科夫場中結點間的傳遞來計算目標結點的置信度,將其引入TOP-N推薦系統能避免上述問題。另外,考慮到BP算法在計算置信度時采用全局的結點,有較大的冗余計算,因此先將其優化改進,采用自適應大小區域內的結點計算置信度,然后引入推薦系統[14~15]建立新模型:將用戶集和項目集作為兩個結點集合建立二分圖,用戶對項目的評分作為用戶結點和項目結點的邊緣閾值,通過置信度在項目結點和用戶結點之間的傳遞來迭代計算目標結點置信度,根據最終置信度大小生成排名列表。通過實驗發現,改進后的BP算法在不損失精度的前提下,效率遠高于傳統BP算法,并且在Precision值和Recall值和MAP值三方面均優于協同過濾算法和基于RWR的方法。
2 BP算法
置信度傳播算法是基于馬爾科夫隨機場的一種近似計算,馬爾科夫場中的結點是成對的,分為隱式和顯式兩個狀態。置信度傳播算法利用迭代的算法在結點與結點之間傳遞信息,從而利用這些信息及當前結點的狀態來推斷相鄰結點的狀態,進而更新當前整個馬爾科夫場的標記狀態,它可以解決概率圖模型的概率推斷問題,且所有問題并行實現,多次迭代后,所有結點的置信度不再發生變化,達到最優狀態,此時的馬爾科夫場也達到收斂狀態。
馬爾科夫場的兩個關鍵過程:
1)加權乘積計算所有結點信息;
2)信息在隨機場中的傳遞。
一個結點到另一個結點傳遞的信息叫做信息向量,向量中元素的個數等于該結點可能所處的狀態數目。信息向量的計算由式(1)獲得:

其中,mij(X)表示結點i傳遞給結點j的消息,表示在 X 狀態下,i對j的置信度。N(j)i表示結點 j的MRF一階鄰域中不包含結點i的鄰域。Φi(Y)表示結點i處于Y狀態下的結點勢能。Ψij(Y,X)表示當j的鄰結點i處于Y狀態時j處于X狀態的概率,由傳播矩陣獲得,傳播矩陣在4.3節中給出。
圖1演示信息傳遞過程。

圖1 信息傳遞機制
此時,結點i處于狀態X的置信度為式(2)所示:
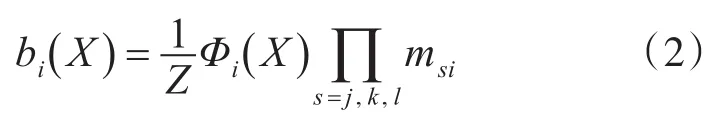
其中,k是歸一化因子,最終的置信度代表結點處于相應狀態的可能性。
3 改進BP算法
在計算目標結點的置信度時傳統BP算法考慮了整個馬爾科夫場中所有結點對當前結點的影響,運算效率低,而如果只考慮以該結點為中心,自適應大小的區域內結點對目標結點的影響,則可以大大降低時間復雜度,從而提高算法效率。
信息在整個馬爾科夫場各結點之間傳遞時,結點之間相互的影響因結點與目標結點距離而存在差異,與目標結點距離較近的結點可能對目標結點影響較強,距離較遠的結點可能影響較弱,所以以目標結點為中心,考慮不同大小區域半徑內的結點對目標結點的影響,結果如圖2所示。

圖2 未收斂結點比例示意圖
由圖2可看出BP算法在馬爾科夫隨機場中不同區域半徑下的結點收斂情況。假設區域半徑為r,即只考慮與目標結點距離小于等于r的結點,該區域內所有結點對目標結點傳遞信息后后者的置信度為mr,同時假設傳統BP算法所對應的區域半徑為l,即r充分大的情況下,該區域內所有結點對目標的置信度為 ml,r=1,2,…,l,設定閾值 ε,當‖mr-ml‖<ε時即可認為是收斂。由圖2可知,每一個結點只需較小區域內的置信度更新即可收斂,所以自適應區域大小的算法可以有效減少傳統BP算法中的冗余計算,所以僅更新未收斂結點的置信度信息,即當‖mr- ml‖<ε時,認為已經達到收斂狀態,此時不再擴大置信度的更新范圍。ε的取值在4.4節中給出。
4 基于改進BP算法的個性化推薦算法
4.1 二分圖模型的建立
創建一個用戶關于項目偏好的二分圖,將用戶集合和項目集合作為兩個結點集合,建立二分圖。結點的狀態分為喜歡和不喜歡兩個狀態。為了提高準確度,設定當評分高于某個閾值時認為用戶喜歡該項目,否則認為不喜歡該項目,當評分高于這個閾值時建立用戶結點和該項目結點的邊,閾值的選擇在5.1節中給出。
4.2 結點勢能的計算
結點勢能是基于項目評分的。因為設定了兩種狀態:喜歡和不喜歡,所以結點勢能也有兩種,每個結點勢能需分配0.1~0.9之間的某個值,并且一個結點的兩個結點勢能的和應該為1。目標用戶的評分越高,在喜歡狀態下的結點勢能就越大。結點勢能由式(3)獲得:
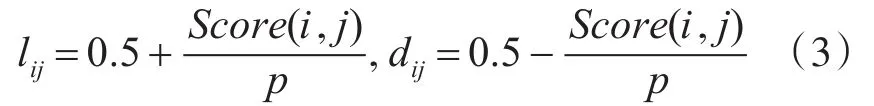
其中,lij表示喜歡狀態下的結點勢能,dij表示不喜歡狀態下的結點勢能,Score(i,j)表示目標用戶i對項j的評分。常數p是歸一化因子。如果獲得的結點勢能低于0.1或高于0.9,用0.1或0.9代替。未被評分項目的結點勢能初始化時在兩種狀態下均分配為0.5。
4.3 傳播矩陣的建立
兩結點間勢函數值Ψij(Y,X)由傳播矩陣獲得,表示當j的鄰結點i處于Y狀態時j處于X狀態的概率。在推薦算法中,將兩個狀態分別設定為喜歡和不喜歡,表1是一個傳播矩陣的例子,為避免數字下溢,α設定為一個很小的值。

表1 傳播矩陣示例
4.4 置信度消息的更新
大部分馬爾科夫場中的結點在受到其某一鄰域范圍內結點的信息傳遞后其置信度是趨于收斂的,改進BP算法僅更新尚未收斂結點的置信度而忽略這些收斂結點。因此在計算置信度過程中無需計算整個馬爾科夫場中所有結點的置信度,而只要在計算前對結點進行收斂判斷,若收斂,則不用計算,若不收斂,則迭代計算其置信度。收斂閾值的選取就顯得尤為重要。如果選取閾值過大,一些尚未收斂的結點會被錯誤判定為收斂結點而停止計算,導致計算結果精度降低;如果選取閾值過小,因為在每次更新置信度時都需要判斷是否收斂,所以會增加計算量,而不能有效提高算法效率。綜上所述,選擇合理的閾值是非常必要的。
為了降低實驗復雜度,對‖mr- ml‖<ε稍作修改,改為判定每個結點在相鄰兩次信息傳遞后的誤差值小于某個特定閾值,即‖bi+1(X)-bi(X)‖<ω,經過多次實驗驗證當ω=1和ω=2時,該算法最優,在實驗部分給出說明。在迭代計算完成后,根據最終置信度大小排名生成列表,選取TOP-N項目列表推薦給目標用戶。
5 實驗和結果分析
實驗數據是由美國明尼蘇達大學GroupLeans項目提供的開源MovieLens數據集,包含72000名用戶對10000部電影的1000萬條評分數據,對電影的評分取1~5之間的整數值,從中選取了包含943個用戶對1682個電影的10000條評分數據進行實驗。實驗數據劃分為訓練集和測試集,訓練集和測試集的比例為4∶1,傳播矩陣中α的取值為0.0001。
5.1 邊緣閾值
在實驗數據集中,用戶對項目的評分值是1到5之間的整數,所以需在該區域內選取值作為結點與結點之間邊緣閾值,為了在實驗中得到更精確的結果,考慮1和5之間(不包含1和5)的整數以及評分的算術平均值和幾何平均值(GM)作為邊緣閾值進行實驗觀察其各項評測指標,實驗結果如表2所示。
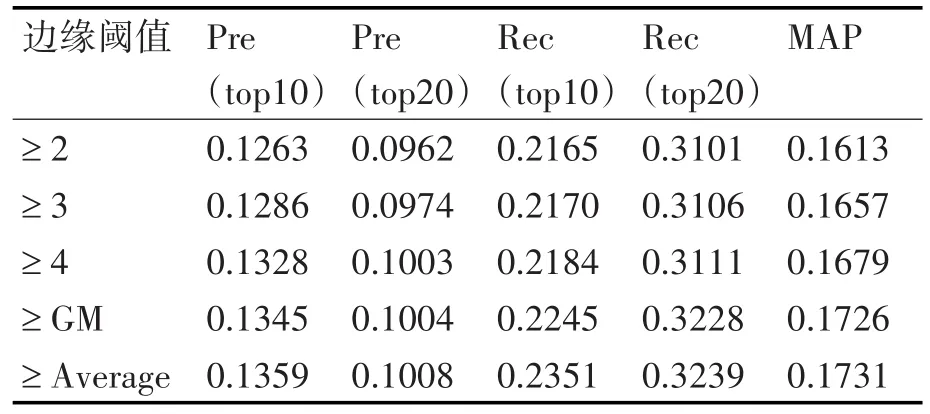
表2 不同邊緣閾值下性能比較
上述實驗為傳統BP算法實驗結果,這是因為,對于改進BP算法或者傳統BP算法,閾值的選擇是可以一致的,從表2可以看出,邊緣閾值取算術平均值和幾何平均值的結果最好,相比之下選取算術平均值作為邊緣閾值。
5.2 ω的選擇
將傳統BP算法和參數ω=1,2的改進BP算法的運算時間做對比,即在不同區域半徑下對比三種算法的運算時間,實驗結果如表3所示。
從表3中可以看出:隨著區域半徑的變大,BP算法的運算時間呈線性增長,而改進BP算法的運算時間增長較緩;ω=2的改進BP算法表現效果更好一些(下文均用ω=2的改進BP算法)。

表3 不同半徑區域下的各算法運算時間比較
5.3 與傳統BP算法的性能比較
將改進BP算法應用到推薦系統后與傳統BP算法性能比較,實驗結果如表4所示。
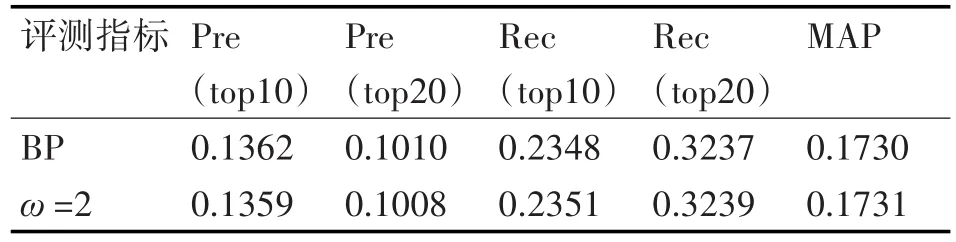
表4 與傳統BP算法的性能比較
從表4可以看出,考慮全局結點的傳統BP算法與改進BP算法在各項性能指標中并無明顯差別,但是結合表3可知,在運算時間上后者明顯優于前者。
5.4 不同推薦算法的性能比較
將基于項目的協同過濾算法中的參數k設置為30,此時該算法的精確度能達到最優。對于基于RWR的方法,將高于用戶平均評分的評分設為邊緣閾值,給目標用戶的重啟向量元素設為1,其他用戶的設為0,重啟概率設為0.15,三種算法在精確度、召回率和MAP值指標的比較如圖3所示。

圖3 不同推薦算法的性能比較
由圖3可看出,基于RWR的方法在精確度、召回率和MAP值三個指標上均遠高于基于項目的算法,這是因為基于RWR的方法采用迭代隨機游走,能夠推斷結點之間的隱式關系。這也是基于項目的算法的一個缺陷。而改進BP算法要優于基于RWR的方法,因為后者只考慮均勻的結點,而BP同時考慮了均勻和異相[16]。另一方面,改進BP算法既計算了目標用戶偏好結點的可能性,也計算了不喜歡結點的可能性。因此,基于改進BP算法的推薦算法優于基于項目的協同過濾算法和基于RWR的方法。
6 結語
將概率統計中的置信度傳播算法改進優化后引入到個性化推薦系統中建立了新的推薦模型,把用戶集合和項目集合分別作為結點集合建立二分圖,通過置信度在馬爾科夫場中的傳遞規律來獲取用戶的偏好,然后根據最終置信度大小排名生成了一個推薦列表給用戶。用自適應大小區域內的結點計算目標結點置信度,比傳統BP算法運算時間更少,同時避免了基于RWR的方法存在的一些不足,又不失推薦項目的多樣性。通過實驗將提出的算法分別與傳統BP算法、基于項目的算法和基于RWR的方法做比較,結果表明,提出的算法在各項評測指標方面表現更好,是一種有效的算法。

