基于字符特征的數字字符識別?

郝學智 張愛梅 姚鵬威 黃 曉 吳國棟

（鄭州大學機械工程學院 鄭州 450001）

1 引言

數字字符識別是光學字符識別（OCR）的一個重要分支［1］，在車牌號碼、名片、身份證號碼、銀行卡號、快遞號、支票號碼、郵政編碼以及其他編號識別方面具有重要的實用價值和廣闊的市場潛力。因此吸引了大量的研究人員進行深入的研究，并提出了不少識別算法。在有關數字識別的大型系統中，數字識別大部分采用BP算法［2］（神經網絡算法）或者SVM算法（支持向量機算法），但這些方法計算量比較大，為實現高效率對硬件要求較高，實現起來還非常復雜，且在純數字識別的系統中顯得大材小用，而很多純數字識別算法需要大量的預處理運算，包含二值化、去噪、均衡化、細化、規整、輪廓提取、字符切割、模板匹配、分類器訓練［3］等，使得識別的運算量成倍增加。

數字字符的識別是光學字符識別中比較簡單的一種［4］，因為字符個數少，只有10個，可以利用字符間不同的特征對其進行分類，按類型逐級識別，直到識別出單個字符。因此只要找出一種能將10個字符分別區分開的特征組合，就可以將數字字符識別出來。作者提出了一種基于字符投影特征進行數字字符定位識別算法。該算法只需對圖像進行簡單的預處理，就可提取特征進行識別。識別過程的框圖如圖1。

2 預處理和識別算法

2.1 預處理

這里進行的預處理，主要便于后面特征提取中進行字符特征的提取和區分向量的分類［5］。分兩步:

1）讀取圖像并對字符圖像進行二值化處理，由于字符圖像的前景與背景相差比較大，可以直接設定閾值進行二值化；

2）使用Hough變換對圖像進行傾斜校正［6］，使用高斯平滑濾波器進行濾波，去除噪聲。

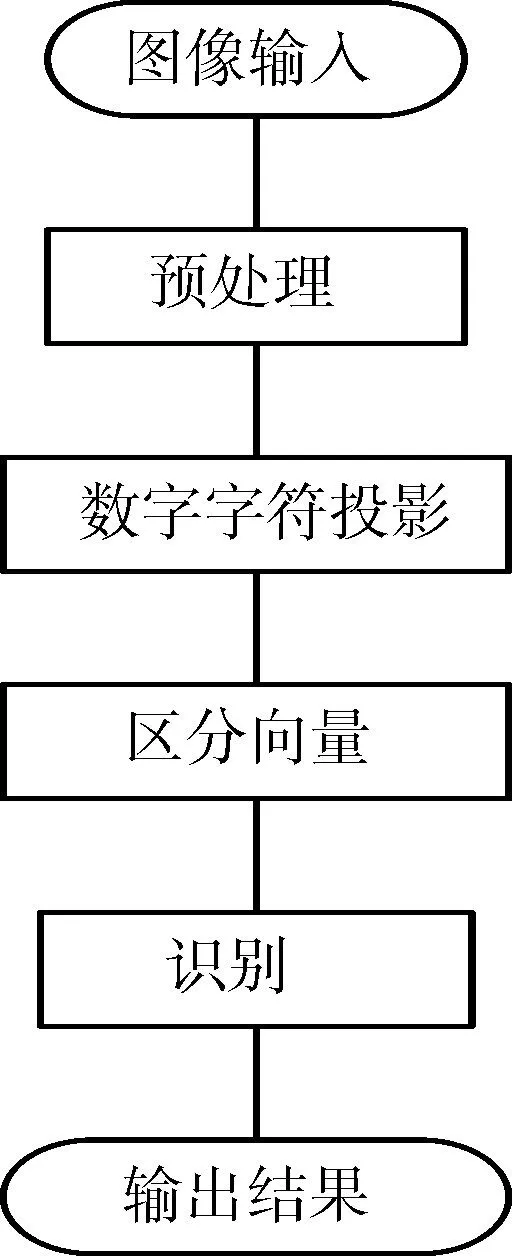
圖1 數字識別原理框圖

經過預處理后，數字字符圖像顯示結果如圖2所示。

2.2 識別算法

2.2.1 圖像投影

圖像對應方向上的投影［7］，就是在該方向取一條直線，垂直于該直線（軸）的圖像上的表示字符像素在該軸該位置的射線積分。圖像投影的數學關系如圖3所示，令 f( )x,y表示圖像函數，穿過的一條線稱為射線。沿某一射線的積分稱為射線積分，而射線積分的集合則組成投影。從坐標原點向射線做一垂線，以此垂線作為新坐標軸t，并構成新坐標系（t，s），（t，s）坐標系由（x，y）坐標系旋轉Θ角得到，兩坐標系關系如式（1）:

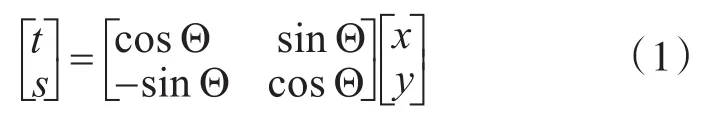
圖3 圖像在角度為Θ方向的投影PΘ(t)

射線積分表達式如式（2）:

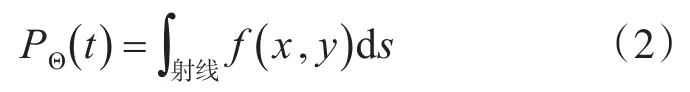
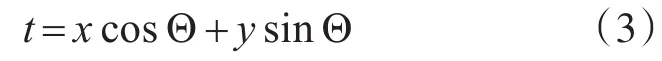
圖4 字符垂直投影

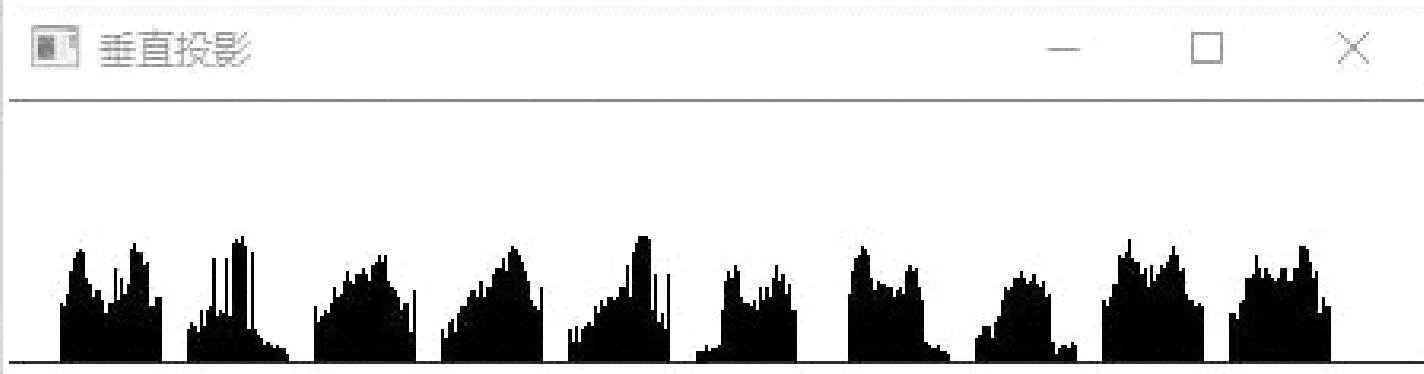
圖5 字符水平投影

基于圖像投影的數字字符定位就是將預處理后的圖像映射成這種特征［8］后，基于這種特征判定圖像中的字符位置（坐標）。這樣就完成了字符的定位工作，便于下一步識別。

2.2.2 “區分向量”識別

區分向量定義為，特定向量與字符相交并將相交次數作為統計特征，對數字字符進行區分辨別的向量稱之為區分向量。

關于區分向量基于字符投影特征對字符進行辨別，在數字圖像處理中，左上角為坐標原點，水平向右記為X軸正方向，豎直向下記為Y軸正方向。在垂直方向Xmax位置，沿Y軸正方向，第i次顏色變換記為 yi，i=1，2，3，4……2n-1，2n；在水平方向Ymax位置，沿X軸正方向，第j次顏色變換記為xj，j=1，2，3，4……2n-1，2n。其中 y2i-1，y2i即第i行字符所在行的豎直方向的位置，x2j-1，x2j即第i行、第j個字符的水平方向的位置。假設第i行第j個字符是數字5，如圖6所示為字符位置。字符位置確定即定位完成后便于進行后續字符的識別。

圖6 第i行第j個字符位置示例

第i行、第j個字符的識別需要三個區分向量，則區分向量所在位置的表達式分別為

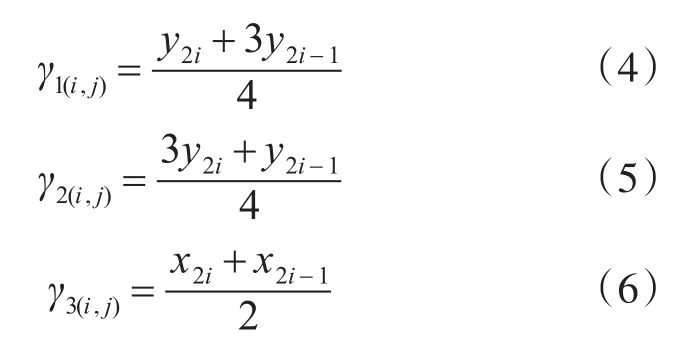
其中，式（4）、（5）中 γ1(i,j)、γ2(i,j)為第i行、第j個字符水平方向的區分向量，式（6）中γ3(i,j)為第i行、第j個字符豎直方向的區分向量。對每個數字字符同時使用水平、垂直區分向量與字符進行相交次數統計，相交次數統計結果分將數字字符為五類，如表1第二列所示:若水平相交次數分別為2、2，而豎直相交次數為2，則為數字為0，單獨一類，直接可得出識別結果；若水平相交次數分別為1、1，而豎直相交次數為1，則數字為1或7，精確識別結果待后續辨識；若水平相交次數分別為1、1，而豎直相交次數為3，則數字為2、3、5其中之一；若水平相交次數為2、2，而豎直相交次數為3，則直接識別為數字8；若水平相交次數分別為2、1，而豎直相交次數為3，則直接辨別為數字9；通過這個結果可以直接辨別出數字字符0、8和9，對于剩余兩類同時記錄水平方向區分向量γ1(i,j)、γ2(i,j)與字符穿越顏色奇數次變換位置的分別記為X1(2i-1,k)、X2(2i-1,k)其中k=1、2（區分向量與字符相交顏色奇次變換最多兩次），并用 X1(2i-1,k)、X2(2i-1,k)與 γ3(i,j)作比較，得出相交位置在γ3(i,j)左側還是在γ3(i,j)右側。即用如下表達式進行辨別:

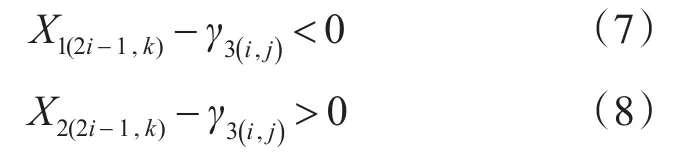
在1，7這一類其中 X1(2i-1,k)、X2(2i-1,k)與 γ3(i,j)相減均小于0的確定為數字1，X1(2i-1,k)、X2(2i-1,k)與 γ3(i,j)相減均大于0的確定為數字7；同樣2、3、5用此方法也可以輕易辨別。

至此，10個數字字符已經全部辨識出來。區分向量結合 X1(2i-1,k)、X2(2i-1,k)與γ3(i,j)大小比較進行 辨 識 ，過 程 見 表 1（ 在 X1(2i-1,k)-γ3(i,j)、X2(2i-1,k)-γ3(i,j)中，0表示區分向量與字符的相交位置在左側即滿足式（7），1表示在右側即滿足式

（8），對已識別出的字符，不再標出）。

2.2.3 識別算法

根據表1可得字符識別的算法如下。

1）求水平和豎直區分向量分別與數字字符的相交次數

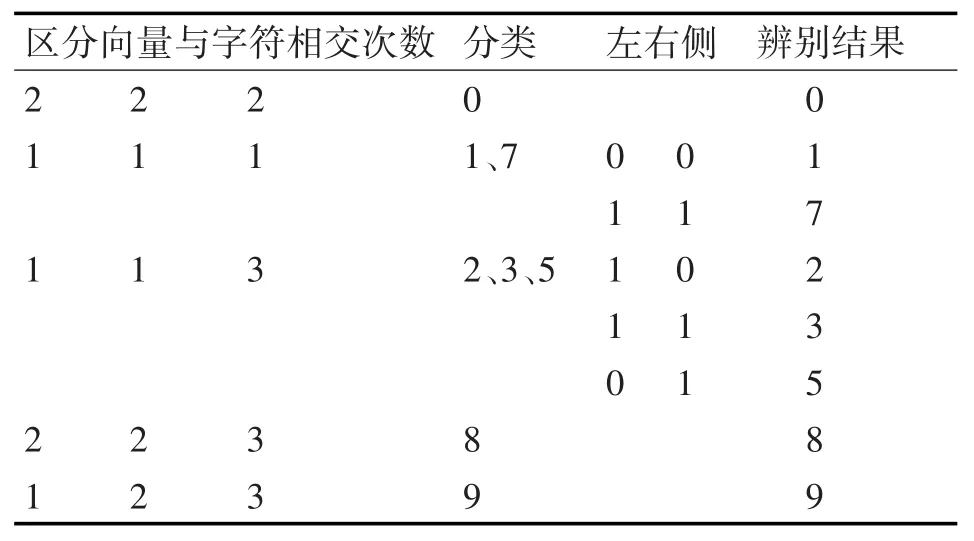
表1 區分向量進行字符識別過程

如果相交次數為 2、2、2，則為數字 0，直接退出；

如果相交次數為1、1、1，，為數字1或7之一，到第2）步；

如果相交次數為1、1、3，則為數字2、3、5之一，到第2）步；

如果相交次數為 2、2、3，則為數字 8，直接退出；

如果相交次數為 1、2、3，則為數字 9，直接退出；

2）相交位置位于豎直區分向量γ3(i,j)左右測判斷

區分向量與字符相交次數為1、1、1，若相交位置均位于 γ3(i,j)左側，即為0、0，則為數字1，退出；

區分向量與字符相交次數為1、1、1，若相交位置均位于 γ3(i,j)右側，即為1、1，則為數字7，退出；

區分向量與字符相交次數為1、1、3，若相交位置均位于 γ3(i,j)右側，即為1、1，則為數字3，退出；

區分向量與字符相交次數為1、1、3，若 X1(2i,k)小于 γ3(i,j)，而 X2(2i,k)大于 γ3(i,j)，即為0、1，則為數字5，退出；

區分向量與字符相交次數為1、1、3，若 X1(2i,k)大于 γ3(i,j)，而 X2(2i,k)小于 γ3(i,j)，即為1、0，則為數字2，退出。

3 算法實現

3.1 字符投影

數字圖像，是以二維數組形式表示的圖像，其數字單元為像元［9］。又稱數碼圖像或數位圖像，是二維圖像用有限數字數值像素的表示。由數組或矩陣表示，其光照位置和強度都是離散的。數字圖像是由模擬圖像數字化得到的、以像素為基本元素的、可以用數字計算機或數字電路存儲和處理的圖像。對圖像的處理的根本就是對二維數組的換算過程。

原圖像經過預處理后變為一個僅有0、1兩個元素的二維數組，對圖像的所有操作轉變為對一個數組或者矩陣的操作［14］，從根本上簡化了圖像的后續處理過程。

水平投影，對于預處理后的圖像，進行從上到下地掃描［10］，如果像素點的像素值為零（經過二值化后，代表字符的像素點的像素值為零，如若為一，則反之），則相對應列的投影位置零像素加一，本質就是旋轉角Θ=π時圖像的射線積分。轉化為數字問題，就是對一個矩陣的操作，遍歷矩陣每一列，尋找所對應列數值為0的個數，然后在對應位置重新繪制投影的過程，即Θ=π時圖像的射線積分外在表現形式。

3.2 字符定位

1）單行統一大小的字符

對預處理后的圖像，對整行數字字符直接進行垂直方向和水平方向的投影［11］，水平投影直接可以判定每個字符的水平位置，垂直投影確定該行字符的豎直位置，即該行每個字符所在的豎直位置，水平和垂直投影相互配合即可判別出字符的位置。

2）單行非統一大小的字符

對預處理后的圖像，數字字符首先進行水平方向的投影，根據水平方向投影，確定每個字符的所的水平位置，進而對每個字符再進行單獨垂直投影，每個字符水平投影和垂直投影相互配合即可判別出該字符的精確位置，即轉變為1）所述的情況。

3）多行統一大小的字符

對預處理后的圖像，數字字符首先進行垂直方向的投影，確定字符所在行的位置，對每行字符再進行水平方向投影，然后就轉變為1）所述情況進行后續處理。

4）多行非統一大小的字符

對預處理后的圖像，數字字符首先進行垂直方向的投影，確定字符所在行的位置，對每行字符再進行水平方向投影，然后就轉變為2）所述情況進行后續處理。

5）雜亂無章的字符

此算法對于雜亂無章的數字字符，還不能有效的精確定位字符的位置，所以此算法還具有一定的局限性，并不適用于此種情況的數字字符識別。

3.3 字符的識別

區分向量為本文定義的一個量，定義為特定向量與字符相交的次數作為特征［12］，對數字字符進行區分辨別的特殊向量稱為區分向量。目的是為了用更加簡單明了的方式識別數字字符，提高程序的魯棒性［13］。

1）區分向量的位置計算

經過大量的統計分析，排除不同字體的干擾，豎直區分向量位置確定在字符所在水平位置的二分之一處；水平區分向量位置分別確定在字符所在豎直位置的四分之一和四分之三處。

2）區分向量與字符相交次數及位置

在字符定位完成，區分向量的位置確定后，在每個字符相應位置、確定的方向分別做區分向量，區分向量與相應字符相交，每相交一次便計數一次。區分向量與字符相交的本質，即遍歷區分向量所在位置的字符相應行或列只有0、1兩個元素的一維數組，形似向量一樣與相應字符相交，并且記錄水平區分向量中像素值由1轉變為0的奇數次坐標位置和垂直區分向量的坐標位置。

水平區分向量與字符相交的奇數次坐標位置的橫坐標，與垂直區分向量的橫坐標作比較，如果水平區分向量與字符相交的奇數次坐標位置的橫坐標小于垂直區分向量的橫坐標，即水平區分向量與字符相交位置位于垂直區分向量左側，否則位于右側，這就實現了對字符的區分和辨別。

4 結語

作者使用Visual Studio調用Intel的開源視覺庫Open Source Computer Vision Library（OpenCV）對該算法進行了模擬［14］，通過對大量字符的識別，證明了本算法的可行性和正確性［15］。區分向量的提出和使用提高了程序的魯棒性，降低了數字字符識別的難度，此算法不僅適用于單行數字、多行數字、統一大小或非統一大小的數字，而且儀表盤數碼管中數字字符識別依然適用。因此，本算法也可用于其他的計算機識別中［16］。