自適應數據驅動的緊框架微地震數據隨機噪聲壓制
唐 杰 張文征 梁雨薇 谷玉田
(①中國石油大學(華東)地球科學與技術學院,山東青島 266580; ②中國石化勝利油田油氣勘探管理中心,山東東營257000)
0 引言
微地震監測技術是通過監測致密儲層壓裂改造產生的微地震事件,以評價與分析儲層改造效果的一種地球物理技術[1]。微地震震源能量相對較弱,信號在傳播過程中能量又被地層強烈吸收,造成微地震事件湮沒在噪聲中,所獲得的資料通常存在微震事件少、有效信號能量弱、信噪比低等缺點[2]。為了有效地提高初至拾取的精度及反演結果的可靠性,需要壓制微震資料中的隨機噪聲,提高數據的信噪比[3]。
微地震信號的去噪方法有很多,根據微地震監測方式的不同,可分為井中微地震資料去噪及地面微地震資料去噪兩大類[4],前者去噪結果信噪比相對較高,后者的信噪比較低。微地震數據中的不規則干擾和有源噪聲類型非常多,包括壓裂井場干擾、抽油機噪聲、鉆機干擾、建筑工地噪聲、工業電干擾、車輛噪聲、風吹草動、人畜活動和物體墜落噪聲等。近年來針對井中微地震數據的主要去噪方法包括偏振濾波、τ-p變換、F-K濾波等[5-6]; 針對地面微地震數據當前有效去噪方法主要包括基于獨立分量分析的方法、基于局部相關譜約束的多道匹配追蹤算法、基于壓縮連續小波變換方法及基于多尺度形態學的方法等[7-11]。由于地面微地震資料具有強噪聲、弱有效信號的特點,很多常規的去噪方法難以得到理想的去噪效果,因此研究針對地面微地震資料的去噪方法也十分重要。
稀疏表示(稀疏編碼)是壓縮感知理論的先驗條件,能夠從多維數據中自適應地構造字典,通過該字典的線性組合表示地震數據。稀疏表示理論的關鍵問題包括字典構造方法及稀疏優化方法,字典構造就是確定字典中的基函數,基函數的性能決定了信號表示的稀疏程度。姜宇東等[12]采用曲波變換算法進行了微地震數據的自適應閾值噪聲壓制, Zhang等[13]研究了基于三維Shearlet變換的多分量微地震去噪方法,兩種方法都是基于固定基的稀疏變換。固定基的稀疏變換沒有利用地震數據的先驗信息,而字典學習方法通過原始數據訓練得到稀疏變換,將字典的訓練與去噪過程有機地結合,能夠實現在數據稀疏表示的同時壓制數據中的噪聲。李穩等[14]研究了基于稀疏分布特征的井下微地震信號識別與提取方法; Tang等[15]研究了基于學習型超完備稀疏表示的隨機噪聲壓制方法,可以有效地壓制偽吉布斯現象引起的擾動; Chen 等[16]研究了基于雙稀疏字典的地震信號去噪方法,獲得了較好的去噪效果; Liang等[17]采用數據驅動緊框架方法完成了地震數據的重構。
針對地面微地震數據的特征,本文利用基于弱紋理塊的噪聲估計方法求取含噪微地震數據中的噪聲方差,采用具有多分辨率性質和冗余性質的數據驅動緊框架方法進行微地震資料去噪,取得了較好的去噪效果。
1 基本理論與技術流程
1.1 基于弱紋理塊的噪聲方差估計
在去噪算法中,需要知道噪聲的分布模型和統計參數,噪聲的方差估計是含噪數據處理中的常見問題之一[18]。目前有代表性的噪聲估計算法有很多,常見的有基于小波分解的噪聲方差估計、基于主成分分析的方差估計[19]、基于尺度不變性的噪聲估計方法[20]及基于弱紋理塊的噪聲方差估計[21]等。小波變換估計方法是對數據進行小波變換,數據的能量主要集中在尺度大的子帶,而尺度小的高頻子帶系數的幅值較小、能量較低。因此,當噪聲較大時,可將最高頻率子帶的系數全部看成是噪聲,由此估計噪聲的標準方差,但當噪聲較強時小波變換的估計誤差較大。
基于弱紋理塊的噪聲方差估計利用概率統計思想,通過統計數據分割結果擬合每個分割塊的標準差。該方法把含噪聲的地震記錄x看成N個有效信息塊和噪聲塊的組合
xi=si+nii=1,2,…,N
(1)
式中:si是第i個無噪聲的有效信號塊;ni是第i個噪聲塊,假設噪聲獨立于有效信號。將含噪數據塊協方差矩陣的最小特征值分解為
(2)
實際上λmin(Σs)是未知的,基于弱紋理塊的噪聲方差估計就是利用局部梯度矩陣及其統計特性的紋理強度來選擇弱紋理塊,用弱紋理塊集合的協方差矩陣的最小特征值代替式(2)中的無噪數據塊的λmin(Σs),進而求得噪聲方差。數據塊的紋理強度ξi定義為
ξi=tr(Cxi)
(3)

圖1為基于弱紋理塊方法與小波分解方法的噪聲方差估計結果對比,可以看出,基于弱紋理塊方法的噪聲估計結果要優于小波分解估計結果,穩定性較好,基本不會受到實際噪聲水平的影響。

圖1 基于弱紋理塊與小波分解的噪聲方差估計對比
1.2 數據驅動緊框架方法原理
緊框架基的多分辨率性質和冗余性質有助于數據的稀疏表示,數據驅動緊框架優化的目標函數[22-23]為
滿足WTW=I
(4)

(1)稀疏編碼——固定W,求v
(5)
這一步可通過閾值法求解。
(2)字典更新——固定v,求W
滿足WTW=I
(6)
這一步存在顯式解。首先將vxT進行奇異值分解,即vxT=UDXT,則W(k+1)=XUT/r。其中U為m×m階正交矩陣,其每一列為vxT(vxT)T的特征向量;X為r2×r2階正交矩陣,其每一列為(vxT)TvxT的特征向量;D為m×r2階對角陣,對角線上的元素是矩陣vxT的奇異值。
經過k次迭代后,適應于數據x的緊框架被定義為
(7)
具體實施步驟[27-28]如下:




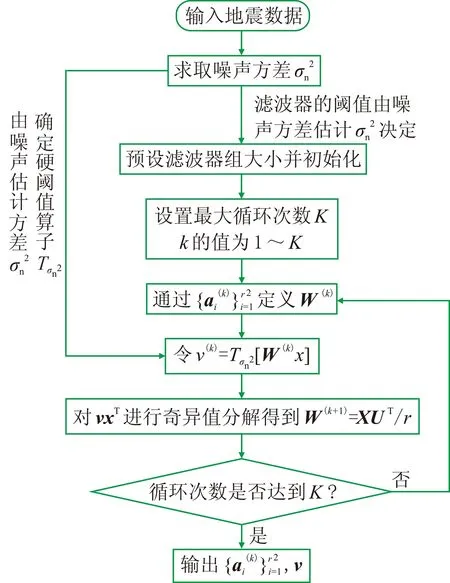
圖2 緊框架濾波器組構建流程
2 理論模型測試分析
2.1 單炮數據模型
為了驗證本文去噪算法的可行性和有效性,建立如圖3所示的速度模型。震源位于(750m,750m)處,在地表處接收,品質因子Q=50,采用黏聲有限差分方法合成的微地震數據如圖4a所示。首先根據合成微地震數據中有效信號的能量加入噪聲,含噪數據如圖4b所示,其信噪比大幅降低。為了對比數據驅動緊框架方法與傳統去噪方法的去噪效果,首先對加噪數據進行曲波閾值去噪,結果如圖4c所示,圖4d為去除的噪聲。然后采用數據驅動緊框架方法去噪,結果如圖4e所示,圖4f為去除的噪聲。從圖4可以看出,經過曲波閾值去噪方法處理后,噪聲雖然被壓制,但是去噪剖面上引入背景斑塊,部分有效信號被壓制,去噪效果不理想;數據驅動緊框架方法的去噪剖面上噪聲基本被壓制,信噪比得到提升,殘差剖面上基本沒有有效信號的殘留,說明本文方法在去噪的同時能夠較好地保護有效信號。

圖3 速度模型


圖4 理論合成數據測試

圖5 預設塊參數r對去噪結果的影響分析(a)及不同噪聲方差條件下的去噪效果分析(b)
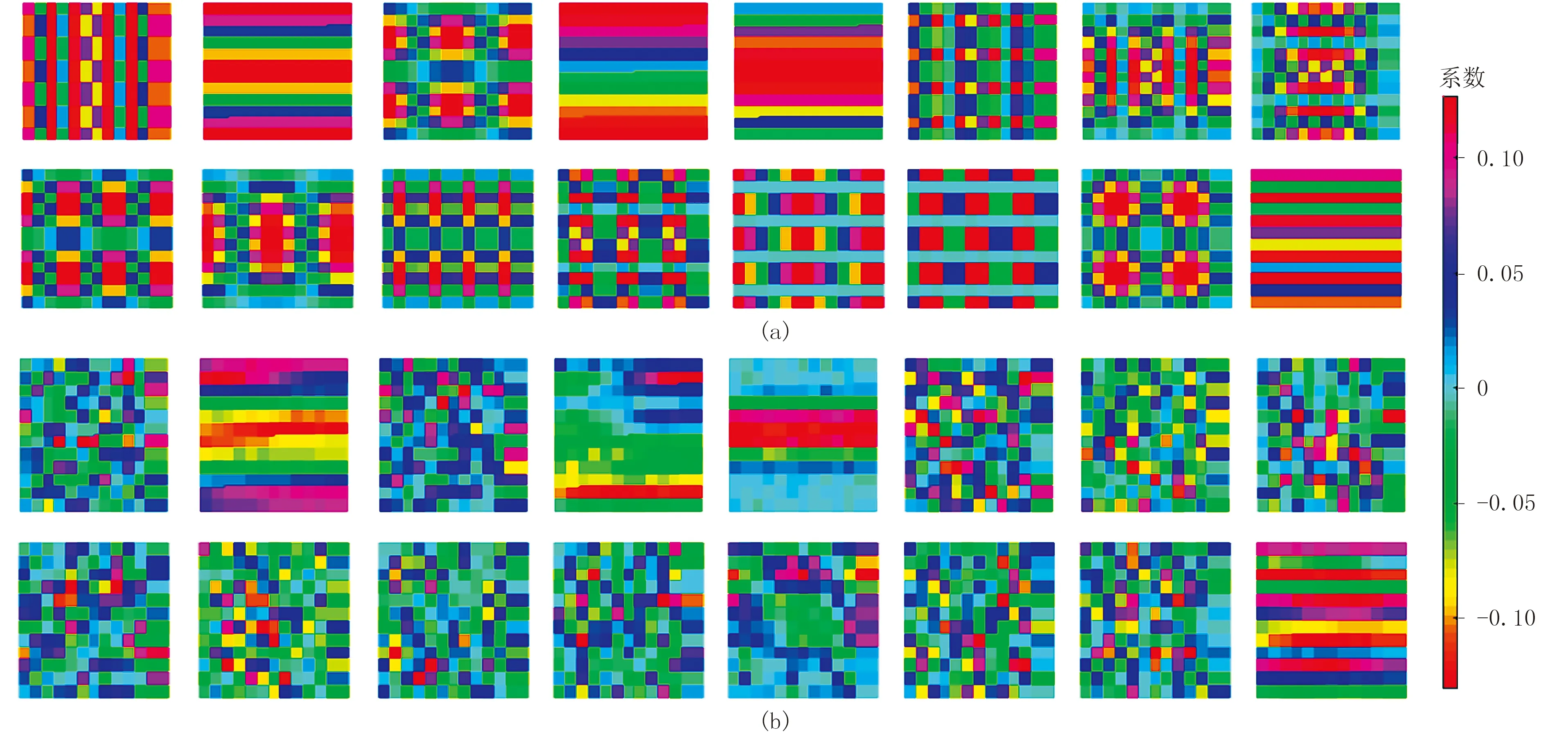
圖6 訓練前(a)、后(b)濾波器組
2.2 復雜數據模型
為了驗證該方法對低信噪比復雜地震數據的應用效果,在圖7a所示的地震記錄中加入噪聲,得到圖7b所示數據。采用數據驅動緊框架去噪方法進行處理,結果如圖7c所示。可以看出,該方法可以有效地壓制剖面中的隨機噪聲,同時能保護邊緣處不連續性信息,斷點及尖滅點處的同相軸沒有發生畸變,彎曲同相軸處的能量也沒有損失,說明該方法在彎曲同相軸以及斷層等處具有較好的保邊效果。
圖8為含噪數據和去噪數據的相干體屬性和瞬時頻率計算結果。從相干體屬性圖上可以看出,去噪前地震相干體剖面較為雜亂,難以識別斷層和巖性突變點,去噪后這些信息可以從剖面中拾取。從瞬時頻率屬性圖上可以看出,去噪處理后瞬時頻率得到了平滑,較好地壓制了毛刺現象。

圖8 復雜數據模型去噪效果分析
3 實際資料處理
為了驗證本文方法對實際地面微地震監測數據的應用效果,對實測的微震監測數據進行處理。圖9a為原始微地震資料,有效信號完全淹沒在隨機噪聲中,各道間的相關性較差,難以有效地拾取到有效信息,嚴重影響反演結果的可靠性。采用數據驅動緊框架方法進行去噪處理,結果如圖9b所示,可見去噪后的剖面中背景噪聲得到了有效的壓制,連續性較好,信噪比顯著提高,可以清晰地得到微震事件的波形,提高旅行時拾取的精度,為震源定位提供有效數據。圖9c為去除的噪聲,去除的噪聲中沒有摻雜有效信號,有效信息得到了很好的保留。
圖10a為原始微地震記錄單道時頻分布,圖10b為去噪后的單道時頻分布,可以明顯看出:在去噪前的時頻分布中有效信號(圖10a紅色箭頭所示)的能量較弱,噪聲能量強,有效信號被淹沒在噪聲中,很難識別;去噪處理后,噪聲得到很好的壓制,突出了有效信號(圖10b紅色箭頭所示),有效提高了微地震數據的信噪比,在時頻圖中更易識別微地震事件,保障了較高的微地震事件初至拾取精度和定位準確度。

圖9 實際微地震數據壓噪結果
圖11為微地震記錄單道信噪比譜,可見,去噪之后數據的信噪比要明顯大于去噪前的數據,尤其在中、低頻區信噪比提升顯著。
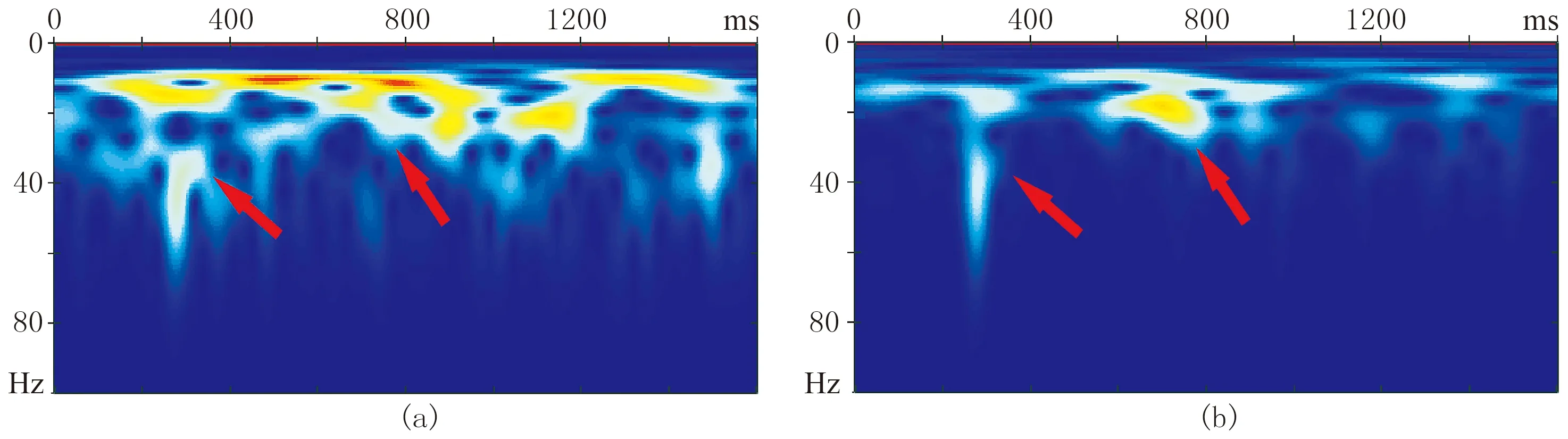
圖10 實際微地震數據壓噪前(a)、后(b)單道時頻分布

圖11 實際微地震記錄去噪前、后信噪比譜
4 結論
本文研究了基于數據驅動緊框架方法在地面微地震隨機噪聲壓制中的應用。通過理論模型及實際資料的處理結果得到如下的結論與認識。
(1)地面微地震監測數據噪聲干擾嚴重、信噪比低,制約著地面微地震監測技術的應用,基于自適應數據驅動緊框架的去噪方法能夠根據微地震數據中的噪聲方差,對微地震數據中的噪聲進行有效的壓制,實現對微地震數據信噪比的有效提升,有助于后續的微地震數據處理。
(2)稀疏表示方法假設原始數據的方差已知,且方差的微小變化會對去噪結果產生較大的影響,需要解決方差的選取問題,基于弱紋理塊的噪聲估計結果優于小波分解估計。
(3)數據驅動緊框架方法具有多分辨率性質和冗余性質,應用于去噪處理,既能夠顯著提高地震資料的信噪比,同時也能夠有效保護有效信號,特別是對于復雜構造地區,該方法能充分保留地震資料中的不連續性信息。對實際微地震數據去噪后可以清晰地得到微震事件的波形,提高旅行時拾取的精度,為微地震震源精確定位奠定基礎。

