艦船氣泡尾流中氣泡的諧振頻率分析

王 眾，張洪剛

艦船氣泡尾流中氣泡的諧振頻率分析

王 眾，張洪剛

（海軍工程大學兵器工程學院，武漢 430033）

為了解決使用明納特頻率在計算艦船氣泡尾流中微小氣泡的諧振頻率時存在的誤差，得到艦船氣泡尾流中微小氣泡更準確的諧振頻率計算公式。本文在中等大氣泡的諧振頻率計算公式明納特頻率的基礎上，根據Rayleigh-Plesset方程，推導了適用范圍更廣的諧振頻率計算公式，并給出了迭代解，以及適當范圍內的二次迭代解。該計算公式可以對艦船氣泡尾流中存活時間最久的微小氣泡的諧振頻率進行計算，對聲尾流制導魚雷的頻率選用具有一定的指導價值。

艦船尾流 氣泡 明納特頻率 諧振頻率

0 引言

艦船在海面上航行的時候都無可避免的會因為艦艏興波破浪將氣泡卷入海水和艦艉螺旋槳高速旋轉而空化產生氣泡而形成長長的尾流，因此利用艦船尾流區同周圍海水介質的不同物理性質探測艦船的尾流制導魚雷應運而生[1-3]。對艦船尾流特性的研究早已受到各個海洋大國的重視，其關系到未來水下反艦的研制與應用[4]。

艦船氣泡尾流具有特定的氣泡分布，可通過聲、光等措施對其進行探測及跟蹤[5]。采用聲措施探測艦船尾流的存在及跟蹤攻擊艦船的武器聲尾流制導魚雷，聲尾流制導魚雷是通過在水中向上發射高頻聲波，再采集回波后進行分析對艦船進行探測及跟蹤的[6]。提高聲尾流制導魚雷對氣泡尾流的探測能力是提高聲尾流制導魚雷作戰效能的重要手段，對氣泡尾流的探測就是對氣泡尾流的散射能力的檢測。氣泡尾流中含有數量眾多的大小各異的氣泡，當聲波頻率能夠使尾流中占大多數的氣泡產生諧振時，氣泡尾流的散射能力最強[7]。現在，大部分使用的氣泡諧振頻率公式是由明納特推導的[8]，該公式對中等大氣泡適用，對于艦船氣泡尾流中能夠長時間存在的微小氣泡適用性不是很強，所以對艦船氣泡尾流中氣泡的諧振頻率進行研究十分重要。

1 氣泡的諧振

液體中的氣泡一旦受到入射聲波的激勵使之從靜止狀態開始擾動后，在不受入射聲波進一步激勵的情況下，會在液體中以其固有頻率脈動。如果入射聲波的頻率和氣泡的固有頻率相同，那么氣泡會發生諧振，此時氣泡脈動具有最大的振幅。我們將此頻率稱為氣泡的諧振頻率，明納特推導了對中等大氣泡適用的諧振頻率0(a)簡化表達式為

式中為氣泡半徑；α為氣泡內氣體比熱比；P為氣泡所受壓強；ρ為液體密度。明納特關系式只適用于較大氣泡以及入射聲波頻率較低的情況，對于較小的氣泡，由于其諧振頻率較高，需要對熱傳導和表面張力的作用進行修正。

在密度為ρ和切變黏度為η的不可壓縮介質中，瞬時半徑為的球形氣泡的運動滿足Rayleigh-Plesset方程，即

式中，0()為無限遠處聲壓，w()為氣泡內壓強的總和，η為液體的切變黏度。

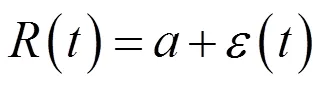
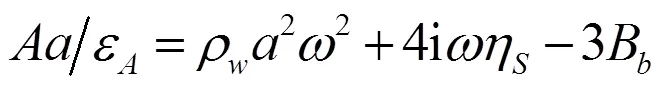
根據體積彈性模量的定義，有

如果假設熱擴散率a可以忽略，且表面張力的影響不受絕熱條件控制，若用ω表示處于絕熱條件下氣泡的諧振頻率，有

用ω表示處于等溫條件下氣泡的諧振頻率，有

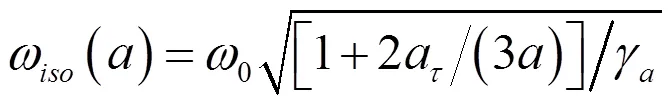
式用于可忽略熱傳導且表面張力起顯著作用的較大氣泡，用于半徑較小氣泡。通常情況下，氣泡脈動既不完全是絕熱脈動也不完全是等溫脈動，氣泡的諧振頻率一般在ω與ω之間。

2 多方指數

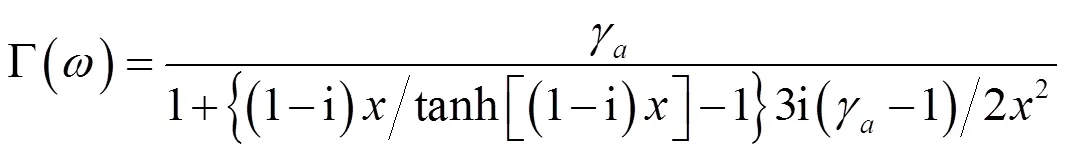
3 氣泡的諧振頻率

對于較大氣泡，其諧振頻率為明納特頻率，但是對于較小氣泡，一方面由于氣泡內部的熱傳導作用，會降低其諧振頻率；另一方面由于氣泡的表面張力的存在，會增加其諧振頻率。由于兩種情況對氣泡的諧振頻率作用效果相反，故需要討論氣泡的實際諧振頻率。

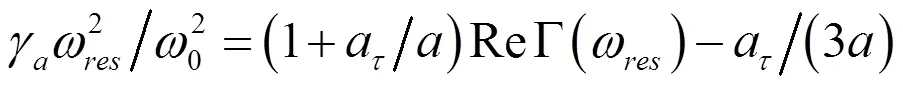
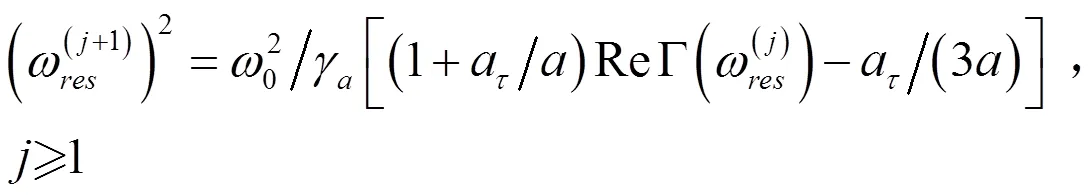
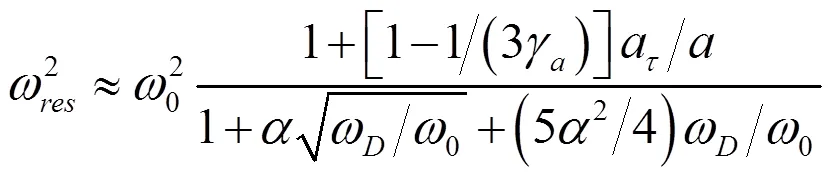
式中，被省略的最大項與和同階。當氣泡半徑大于20μm時，是可忽略的。圖1和圖2分別畫出了海面和深度為90 m處，重復利用式 之后得到的氣泡諧振頻率收斂迭代解，以及通過式計算得到的氣泡諧振頻率二次迭代近似解，還有通過式和式計算的在絕熱和等溫條件下的氣泡諧振頻率ωad和ωiso，并通過除以明納特頻率ω0進行歸一化處理。

圖2 深度90米時，水中氣泡的諧振頻率與氣泡半徑的關系

表1 物理量常數值

從圖1和圖2中可以看出，當氣泡半徑超過20時，根據式計算出的二次迭代解與多次迭代得到的結果基本重合，說明所舍去的高次項對結果幾乎無影響。同時從圖中還可以看出，當氣泡半徑超過3時，直接采用明納特頻率所帶來的誤差小于10%。對于整個氣泡半徑范圍來說，氣泡較小時使用式，氣泡較大時使用式是個很好的選擇，整體誤差小于3%。

4 氣泡的諧振半徑

實際應用中，遇到的往往是由不同氣泡半徑氣泡組成的氣泡群，而不是單個氣泡。前面節討論了不同氣泡半徑氣泡對應的諧振頻率，這一節討論在任意頻率平面聲波入射氣泡群時，什么半徑的氣泡會發生諧振。我們知道，對于較大氣泡，其諧振頻率為的明納特頻率，將明納特頻率表達式轉換成氣泡半徑與頻率的關系如下：

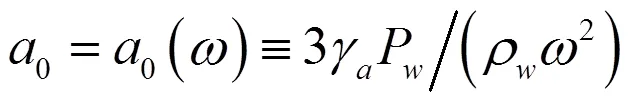
將式記為明納特半徑，那么當聲波頻率低于10 kHz時，諧振氣泡半徑等于明納特半徑。對于更高的聲波頻率，同樣需要在兩個方面對諧振半徑進行修正，一方面是由于氣泡內部的熱傳導作用，會減小其諧振半徑；另一方面由于氣泡的表面張力的存在，會增加其諧振半徑。

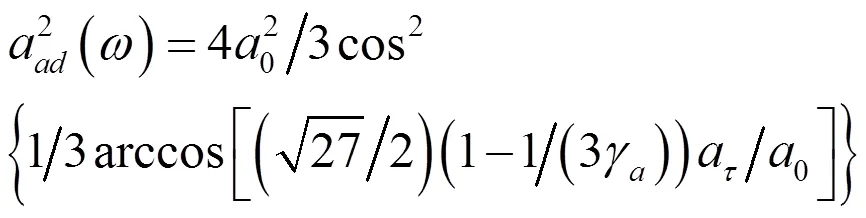
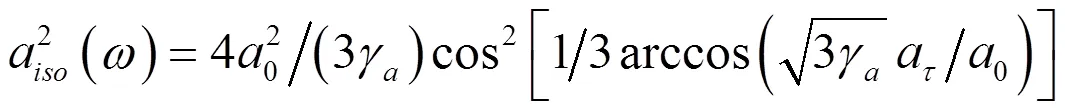
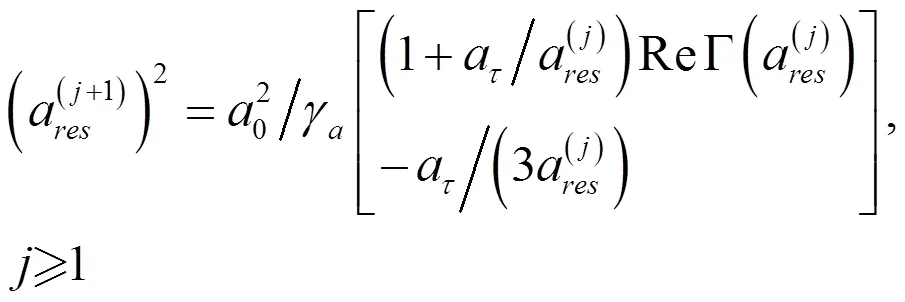
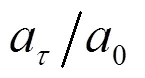
和與被省略的最大項同階，在聲波頻率低于100 kHz時，是可忽略的。

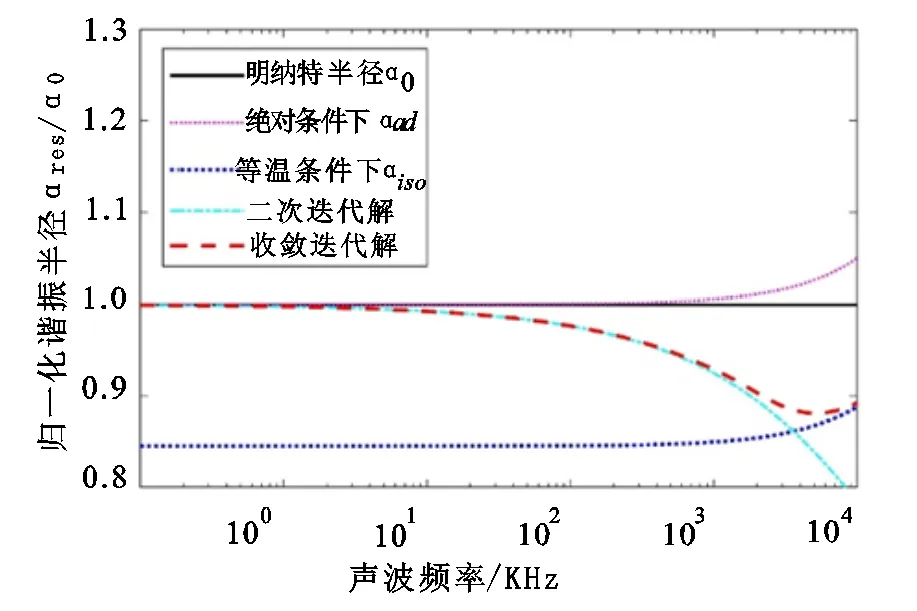
圖4 深度90米時，水中氣泡的諧振半徑與聲波頻率的關系

圖3和圖4分別畫出了海面和深度為90 m處，重復利用式之后得到的氣泡諧振半徑收斂迭代解，以及通過式計算得到的氣泡諧振半徑二次迭代近似解，還有通過式和式計算的在絕熱和等溫條件下的氣泡諧振半徑和α，并通過除以式明納特半徑α進行歸一化處理。計算所用物理量的常數值同樣見表1。

從圖3和圖4中可以看出，當聲波頻率低于在200 kHz時，根據式計算出的二次迭代解與多次迭代得到的結果基本重合，說明所舍去的高次項對結果幾乎無影響。同時從圖中可以看出，當聲波頻率低于200 kHz時，直接采用明納特半徑所帶來的誤差小于10%。對于整個頻率范圍來說，較高頻率時使用式（15），較低頻率時使用式（17）是個很好的選擇，整體誤差小于3%。

5 結論

本文在中等大氣泡的諧振頻率-明納特頻率的基礎上，根據Rayleigh-Plesset方程，推導了從微小氣泡半徑到大氣泡半徑的諧振頻率迭代表達式，并給出了適用半徑范圍不包括數微米級小氣泡但是更簡單的二次迭代表達式。同時，也推導了適用于全頻域的諧振半徑迭代表達式，可通過入射聲波頻率知道更準確的發生諧振的氣泡半徑大小，同時也給出了頻率范圍小一些但更簡單的二次迭代表達式。對于需要知道準確諧振頻率或者諧振半徑的情況，比如對艦船氣泡尾流中氣泡的探測，用本文的方法選擇聲納頻率更為準確，是提高聲尾流制導魚雷作戰效能的方法之一。

[1] 張靜遠. 水聲探測與聲自導技術[M]. 武漢: 海軍工程大學出版社, 2015.

[2] 張群. 艦船尾流主動聲特性研究[D]. 西安: 西北工業大學, 2014.

[3] 田晶, 白光富, 江陽. 艦船氣泡尾流散射光斯托克斯特征研究[J]. 紅外與激光工程, 2018.

[4] 何升陽, 張志友, 金良安, 等. 波浪中艦船遠程尾流區氣泡運動研究[J]. 應用力學學報, 2018.

[5] 潘遜. 艦船尾流氣泡特性及聲探測方法研究[D]. 武漢: 海軍工程大學, 2013．

[6] 張建偉, 楊坤濤, 宗思光等. 水中氣泡運動特性及測量[J]. 紅外技術, 2011,33(4): 219-225．

[7] Stanic S，Caruthers J W，Goodman R R，et.al. Attenuation Measurements Across Surface-Ship Wakes and Computed Bubble Distributions and Void Fractions[J]. IEEE Journal of Oceanic Engineering, 2009, 34(1):83-92.

[8] 林巨, 王歡, 謝萍. 基于聲學方法的氣泡分布和海表風速反演[J]. 聲學技術, 2012, 31(4): 162-165．

[9] Trevorrow M V. Measurements of near-surface bubble plumes in the open ocean with implications for high-frequency sonar performance[J]. Journal of the Acoustical Society of America, 2003, 114(5): 2672-84．

Analysis of Resonant Frequency of Bubbles in Ship Bubble Wake

Wang Zhong, Zhang Honggang

(Naval University of Engineering, College of Weapon Engineering, Wuhan 430033, China)

O32

A

1003-4862（2019）09-0014-04

2018-03-01

王眾（1989-），男，博士研究生。研究方向：武器制導與控制技術。Email: dtoubaby@163.com