發揮學科特點 加強能力考查
林惠彬

摘 要:數學能力是數學素養的重要組成部分,而高考作為最具有引領性的考試,本次考試發揮學科特點,依托基礎知識,加強能力考查,充分體現素養導向。基于能力考查研究2018年高考理科數學全國Ⅰ卷的試題,并根據相關研究給出教學建議。
關鍵詞:能力考查; 試題研究; 高考數學
中圖分類號:G633.6? ? ? ? ? ? ?文獻標識碼:A? ? ?文章編號:1006-3315(2019)04-017-002
高考作為全國最重要的選拔性考試,其核心任務是考查學生的基本學科素養,而學科素養指向學生的能力。就數學學科的選拔性考試命題而言,其任務就是要全面系統地考察學生的數學綜合能力,而高考數學所要考查的能力在《考綱》中的“考試內容”部分以“能力要求”呈現出來,具體包括:空間想象能力、抽象概括能力、推理論證能力、運算求解能力、數據處理能力以及應用意識和創新意識.2018年高考理科數學全國I卷,根據《課標(2017版)》和《考綱》要求,以能力立意,充分發揮數學學科特點,突出基礎知識,強調數形結合思想,注重邏輯推理素養,融入大數據背景,增強實踐性,全面考查了學生的綜合能力。本文從整份試卷總體分析及基于能力的考查這兩個方面展開分析,并在此基礎上給出基于能力考查視角的教學建議。
一、試卷總體分析
1.基礎知識考查分布
為了研究試卷基礎知識考查分布,首先我們必須明確高考數學試卷所涉及的知識內容及其劃分標準,結合有關試題研究的論文資料,以《課標(2017版)》《考綱》和教材為參考,將高考數學試卷(除去選做題部分)中主要考查的基礎知識分為以下12個部分:集合與常用邏輯用語、函數與導數、三角函數、數列、不等式、平面向量、復數、立體幾何、解析幾何、算法初步、計數原理、統計與概率.(注:2018年高考理科數學全國I卷未明顯考察算法初步)各部分知識之間可能會有交叉考查,以下分析以各題考查的主要知識作為該題考查的知識點:
從表格中我們可以看出,此次考試的試題考查范圍廣,幾乎涵蓋了高中數學《課標(2017版)》和《考綱》中要求學生掌握的所有基礎知識,內容結構上與前幾年比保持穩定,以函數與導數、三角函數、平面向量、解析幾何、立體幾何和概率統計六大主干內容為主線,對其他部分內容略有涉及。
2.試卷總體評價
我們可以看到2018年高考理科數學全國Ⅰ卷與前幾年的高考試卷相比在題型上沒有變動,依然是選擇、填空和解答三種題型,且各題型的分值不變;在內容上涵蓋高中大部分知識點,只有少部分非重點知識(如算法、常用邏輯用語、數學歸納法等)此次考試未涉及;整體難度上沒有太明顯的變化,在選擇填空題中難題部分計算要求略有降低,但總體難度沒有大幅調整。此次考試的亮點在于命題方式的創新,根據《考綱》要求,在考題中充分結合實際,并融入數學文化,在考查基礎知識的基礎上,注重對學生能力的考查,充分發揮核心素養的導向作用。
二、基于能力考查的試題分析
1.突出基礎知識,貫穿運算求解能力
高考注重基礎知識的考查,每年高考命題中簡單題的比例一直是最大的,在這其中始終貫穿著運算求解能力。運算求解能力不可以簡單地理解為計算,它還包括對數據、公式的處理變形等。我們可以發現,作為數學考試,幾乎每一個知識點,每一道題目都涉及運算求解能力,只是不同的題目,對學生的運算要求程度不一樣罷了。如第1題依托復數的四則運算、復數的模等知識,考查學生基本運算能力;第15題依托計數原理的知識,以考查學生準確地計數為基本目標,綜合考查運算求解能力;第9題的解答步驟主要涉及聯立方程組求交點坐標,和向量的運算,在考查學生的運算求解能力的同時,也考查了學生的抽象概括能力,是一道難度中等的題目。
2.強調數形結合,體現空間想象能力
對空間想象能力的要求主要體現在:能看得懂圖形,從圖像中提取有效有用信息;會畫圖形,能根據題目條件和實際解題需要畫出適宜的圖形;要求學生能夠從有限的二維紙面——試卷上,對三維圖形進行想象。這就要求我們要將數學知識最重要的兩種表現形式“數”和“形”結合在一起分析,進而解決問題,在本次考試中的許多題均有所體現。如:第7題以三視圖為知識載體,以圖形的分解、組合為考查依托,通過對識圖、畫圖和對圖形的想象能力的考查為主,考查了空間想象能力;第9題以指數函數和對數函數的圖像、復合函數的零點為知識載體,以畫圖和用圖為考查依托,通過對畫圖和對圖形的想象能力的考查,考查了空間想象能力,同時此題融合了分段函數、函數的零點和函數的圖像等知識點,綜合考查學生抽象概括能力、推理論證能力,是一道比較靈活的題目。
3.注重邏輯推理素養,考查抽象概括與推理論證能力
數學是培養理性思維的重要途徑,《課標(2017版)》中也明確提出要培養學生邏輯推理素養,而落實到高考卷中,主要體現為對抽象概括能力與推理論證能力的考查。如第9題的常規解法需要從“g(x)存在2個零點”抽象概括出“f(x)與y=x+a的圖像有兩個交點”,考查了學生的抽象概括能力,運用題目中的條件,合理地得出的取值范圍,考查了學生的推理論證能力;第19題第(Ⅱ)問的求解關鍵在于從“[∠]OMA=[∠]OMB”中抽象概括出“KMA+KMB=0”;第21題以函數的單調性、函數的極值點、函數的圖像、導數在研究函數性質中的應用等知識為載體,綜合考查了推理論證能力。
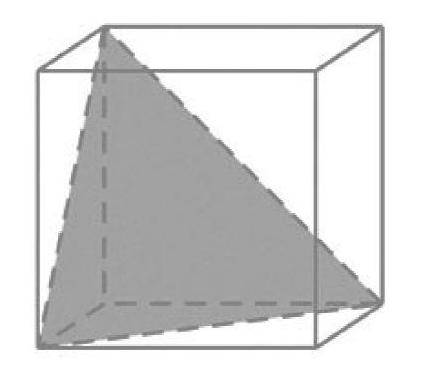
需要特別指出的是本次考試的第12題設計十分精彩,以直線與平面的位置關系為知識載體,以圖形的還原為考查依托,通過對畫圖和對圖形的想象能力的考查為主,考查了學生的空間想象能力的同時糅合了運算求解能力、抽象概括能力和推理論證能力。本題是選擇題的最后一題,相比往年的“壓軸題”,乍一看本題似乎沒有那么高大上,題目信息簡潔明了,也是學生最為熟悉的簡單立體圖形——正方形,解答過程中的計算也不復雜,要求學生認真分析問題、緊抓問題本質,由“每條棱所在直線與平面a所成的角都相等”這一信息抽象概括出“平面a與下圖陰影所在平面平行”,進而進一步推理論證出a截此正方體所得截面面積最大時應該是六邊形,再根據題目所給的正方體邊長進行計算。本題以立體幾何知識為背景,在簡化計算的基礎上,突出考查學生的邏輯推理能力和空間想象能力,充分體現能力和素養導向。
4.融入大數據,加強數據處理能力考查
隨著信息行業的發展,人們進入“大數據時代”后最基本的數據處理、挖掘和應用已成為人的必備技能。數據處理能力要求學生能收集、處理和分析數據,該能力的考查主要體現在概率與統計部分。本次考試第20題依托二項分布、期望等知識,考查數據處理能力,考查用樣本估計總體的思想與方法。這里需要說明的是往年有許多地區、特別是福建省強烈反應,數理統計的題目考查太難,但是我們可以看到,基于《考綱》和《課標(2017版)》中對于應用意識的強調,在2018年的考試中,我們甚至把統計題從原來的20題移到了21題,繼續加大難度。
5.增強實踐性,倡導創新應用意識
數學源于實際生活,其最終目的是解決問題,在本次考試中體現了重視數學應用、關注創新意識的特點。如:第20題以實際生產背景,要求學生深入思考,從中抽取數學模型;第10題創新地以古希臘數學家希波克拉底的研究為背景,將幾何概念和勾股定理融合在一起,回應《考綱》中對于“數學文化”的強調,同時通過優美的圖形向考生展示和傳遞了數學美,更以這種靈活的知識組合方式,強調學生對知識的本質理解,綜合考查空間想象能力、推理論證能力、運算求解能力、應用意識和創新意識。
三、基于能力考查視角的教學建議
1.夯實基礎,歸納總結
基于以上評析,我們可以發現,高考數學中對于基礎知識的考查仍讓十分重視,能力和素養的考查也都是基于基礎知識為載體來體現的,所以教師在教學的過程中,還是要注重學生的基礎知識的教學。當然,注重夯實基礎只能保證學生在簡單題部分的得分,要想學生的能力有進一步的提高,對高中數學知識有整體性的認識并靈活應用所學知識,就要培養學生歸納總結的習慣。
2.深挖本質,關注過程
數學題目千變萬化,但是他們所考查的仍然是符合《考綱》要求的,因為他們的形式可能不同,但所考查的基礎知識和能力都是不變的,這才是試題考查的本質所在。因此,教師在教學過程中要重點關注的是本質的東西,對于知識不能只要求學生進行表面理解,甚至死記硬背,要深入挖掘背后的數學思想方法,這就要求教師在平時關注學生的思考過程,而不是答題結果。
3.聯系實際,注重創新
很多學生覺得數學的學習很難且沒有意義,甚至開玩笑說“買菜需要用到微積分嗎”?關鍵就是在于他們沒有認識到所學的數學知識在實際生活中的應用。教師在教學的過程中應聯系實際,讓學生切身感受數學的實際背景.這幾年,越來越強調創新精神,不管是《課標(2017版)》,還是《考綱》中都體現了創新精神,數學上的創新形式多種多樣,可以體現為試題背景知識創新、知識交匯方式創新、應用方式創新等,要注重培養學生創新意識。
參考文獻:
[1]中華人民共和國教育部.普通高中數學課程標準(2017年版),北京:人民教育出版社,2017
[2]教育部考試中心.2018年普通高等學校招生全國統一考試新課程標準數學科考試大綱〔J〕北京:高等教育出版社,2018
[3]素養導向新舉措能力考查新突破——2018年高考數學試題評析[J]中國考試,2018(07):8-12
[4]晨旭.突出邏輯推理加強應用能力考查——2014年全國高考數學試題評析[J]中國考試,2014(10):14-17
[5]陳美丹.數學能力視角下的試題研究及啟示[D]福建師范大學,2015
[6]林虹.新課程背景下海南高考數學試題分析[D]海南師范大學,2014

