高中數學中的“齊天大圣”

■吳吉云

“齊次式”在高中數學中出現的頻率比較高。對“齊次式”的處理關鍵是化二元為一元,即化繁為簡,化陌生為熟悉。下面我們從多種題型中玩轉“齊次式”,去感受多題一解的奇妙。

1.齊次式在三角函數中的應用

1.1 齊次式在三角函數化簡求值中的應用

小結：當所求式子為關于sinα與cosα的“齊”次分式時,分子分母同時除以cosα或cos2α可以轉化為關于tanα的式子。

1.2 齊次式在正弦定理中的應用

例2設△ABC的內角A,B,C所對的邊分別為a,b,c,若bcosC+ccosB=asinA,則△ABC的形狀為____。

小結：當式子是關于邊a,b,c或關于sinA,sinB,sinC的“齊次式”時,可用正弦定理進行化簡。

2.齊次式在解析幾何中的應用

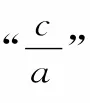
3.齊次式在不等式中的應用

結束語：齊次式在高中數學解題過程中是比較活躍的,在解決相關知識的齊次式時,如果我們能靈活準確地觀察出式子的特征,用減元思想進行化簡,就可以大大提高我們的解題速度和準確度。