數(shù)學(xué)“童畫(huà)”，讓思維的軌跡更清晰

李艷梅

[摘 要]數(shù)學(xué)“童畫(huà)”是一種可視化的學(xué)習(xí)方式，它主張學(xué)生學(xué)會(huì)用數(shù)學(xué)的眼光把握、抽象事物的本質(zhì)，用圖式的方式表達(dá)思維過(guò)程。通過(guò)數(shù)學(xué)“童畫(huà)”表示、說(shuō)明、示意、猜測(cè)，讓內(nèi)涵“顯出來(lái)”，讓發(fā)現(xiàn)“說(shuō)得清”，讓思路“看得見(jiàn)”，讓推理“說(shuō)得通”，讓特征“說(shuō)得準(zhǔn)”，從而讓學(xué)生思維的軌跡更清晰。

[關(guān)鍵詞]數(shù)學(xué)“童畫(huà)”;思維軌跡;看得見(jiàn)

[中圖分類(lèi)號(hào)] G623.5 [文獻(xiàn)標(biāo)識(shí)碼] A [文章編號(hào)] 1007-9068（2019）26-0033-03

數(shù)學(xué)“童畫(huà)”是一種可視化的學(xué)習(xí)方式，是用感性的方式表達(dá)理性的思維。數(shù)學(xué)“童畫(huà)”主張學(xué)生用數(shù)學(xué)的眼光把握、抽象事物的本質(zhì)，用圖式的方式表達(dá)思維的過(guò)程。現(xiàn)結(jié)合教學(xué)實(shí)際，談?wù)勅绾瓮ㄟ^(guò)數(shù)學(xué)“童畫(huà)”，讓學(xué)生思維的軌跡更清晰。

一、“童畫(huà)”表示讓內(nèi)涵“顯出來(lái)”

在核心素養(yǎng)下，數(shù)學(xué)教學(xué)要注重?cái)?shù)學(xué)思想的滲透，特別是在小學(xué)階段，數(shù)形結(jié)合思想的滲透更為重要。形是一種直觀形式，學(xué)生能看得見(jiàn)，并能借助圖形把一些概念和定律的內(nèi)涵挖掘出來(lái)，有助于對(duì)一些概念和定律的理解。在理解中記憶和在理解中應(yīng)用是進(jìn)一步對(duì)知識(shí)的內(nèi)化和深化，特別在“復(fù)習(xí)與整理”這一環(huán)節(jié)，讓學(xué)生把對(duì)知識(shí)的理解用顯性的圖畫(huà)表示出來(lái)，是對(duì)所學(xué)知識(shí)進(jìn)行整合的過(guò)程，更是進(jìn)一步建構(gòu)知識(shí)的過(guò)程。

例如，教學(xué)蘇教版教材四年級(jí)下冊(cè)“運(yùn)算定律”整理與練習(xí)第一課時(shí)時(shí)，我先讓學(xué)生對(duì)所學(xué)的運(yùn)算定律進(jìn)行分類(lèi)整理，然后提問(wèn)：“你能用‘童畫(huà)表示出每個(gè)運(yùn)算定律嗎？”學(xué)生紛紛表示“能夠用‘童畫(huà)表示”，并認(rèn)真繪畫(huà)。在學(xué)生的“童畫(huà)”中，多數(shù)是畫(huà)成交換兩條長(zhǎng)度不等的線段的位置，而用長(zhǎng)度不變來(lái)表示加法交換律，用三條長(zhǎng)度不同的線段表示加法結(jié)合律。從“童畫(huà)”中可看出，對(duì)于三個(gè)數(shù)相加，可以先把前兩個(gè)數(shù)相加再和第三數(shù)相加，還可以先把后兩個(gè)數(shù)相加再和第一個(gè)數(shù)相加，它們的結(jié)果不變。學(xué)生在畫(huà)圖的過(guò)程中體會(huì)到加法結(jié)合律的內(nèi)涵是運(yùn)算順序變了，而結(jié)果不變。用圖表示乘法交換律時(shí)，多數(shù)學(xué)生畫(huà)一個(gè)長(zhǎng)方形，既可用長(zhǎng)乘以寬求出這個(gè)長(zhǎng)方形的面積，也可以用寬乘以長(zhǎng)求出這個(gè)長(zhǎng)方形的面積，因?yàn)槊娣e是相等的，從而凸顯了乘法交換律的本質(zhì)：交換了兩個(gè)乘數(shù)的位置，而結(jié)果不變。同樣的一個(gè)長(zhǎng)方形，可以用兩種不同的方法求出它的周長(zhǎng)，從而得出（a+b）×2=a×2+b×2，促進(jìn)學(xué)生進(jìn)一步理解乘法分配律的意義和模式。

二、“童畫(huà)”說(shuō)明，讓發(fā)現(xiàn)“說(shuō)得清”

學(xué)習(xí)數(shù)學(xué)一定要多問(wèn)“為什么”，解釋“為什么”就是對(duì)知識(shí)的來(lái)龍去脈的梳理，打通新舊知識(shí)的聯(lián)系。依托數(shù)學(xué)“童畫(huà)”的可視性，有助于學(xué)生分析問(wèn)題，把握問(wèn)題的關(guān)鍵，從而使問(wèn)題迎刃而解。

例如，在教學(xué)蘇教版教材五年級(jí)下冊(cè)“分?jǐn)?shù)的基本性質(zhì)”時(shí)，課始我讓學(xué)生在同樣長(zhǎng)的紙條上表示1/2、2/4和4/8，出示問(wèn)題：1/2、2/4和4/8相等嗎？學(xué)生在同樣長(zhǎng)的紙條上分別畫(huà)出它的1/2、2/4和4/8，他們?cè)诋?huà)圖的過(guò)程中對(duì)分?jǐn)?shù)的意義有了進(jìn)一步的理解和深化。從圖中一眼就可看出1/2、2/4、4/8表示的長(zhǎng)度是一樣的，都是表示這個(gè)紙條長(zhǎng)度的1/2，所以很容易得出結(jié)論：1/2=2/4=4/8。接著我追問(wèn)：“它們的分子、分母都不相同，為什么它們的大小卻相等呢？從中你又有什么發(fā)現(xiàn)？”學(xué)生對(duì)照?qǐng)D示分析分?jǐn)?shù)中分子和分母的變化情況，很容易發(fā)現(xiàn)：從左往右看，分?jǐn)?shù)的分子和分母同時(shí)擴(kuò)大2倍，分?jǐn)?shù)的大小不變;從右往左看，分?jǐn)?shù)的分子和分母同時(shí)縮小2倍，分?jǐn)?shù)的大小不變， 從而抽象概括出分?jǐn)?shù)的基本性質(zhì)。我繼續(xù)追問(wèn)：“我們都知道分?jǐn)?shù)和除法有密切的關(guān)系，那么分?jǐn)?shù)的基本性質(zhì)和以前學(xué)過(guò)的什么性質(zhì)是一樣的呢？”學(xué)生對(duì)照?qǐng)D示想到了商不變的性質(zhì)，從而理解了分?jǐn)?shù)的基本性質(zhì)為什么要強(qiáng)調(diào)“0除外”的道理。借助“童畫(huà)” ，學(xué)生能發(fā)現(xiàn)規(guī)律并解釋規(guī)律，找到新知和舊知的內(nèi)在聯(lián)系，從而打通知識(shí)間的聯(lián)系，梳理知識(shí)，掌握規(guī)律，達(dá)到利用“童畫(huà)”說(shuō)明，讓發(fā)現(xiàn)“說(shuō)得清”的效果。

三、“童畫(huà)”示意，讓思路“看得見(jiàn)”

數(shù)學(xué)“童畫(huà)”具有直觀性，能夠幫助學(xué)生理解抽象的語(yǔ)言所描述的復(fù)雜問(wèn)題，利用“童畫(huà)”進(jìn)行直觀示意，把抽象出的典型特征用特定的示意圖表示出來(lái)，可以清晰地得出指向問(wèn)題解決的“思維地圖”，讓思路“看得見(jiàn)”，利于學(xué)生用自己的語(yǔ)言把思維過(guò)程表達(dá)出來(lái)，從而解決了學(xué)生對(duì)抽象的語(yǔ)言描述、符號(hào)意義理解上的困難。

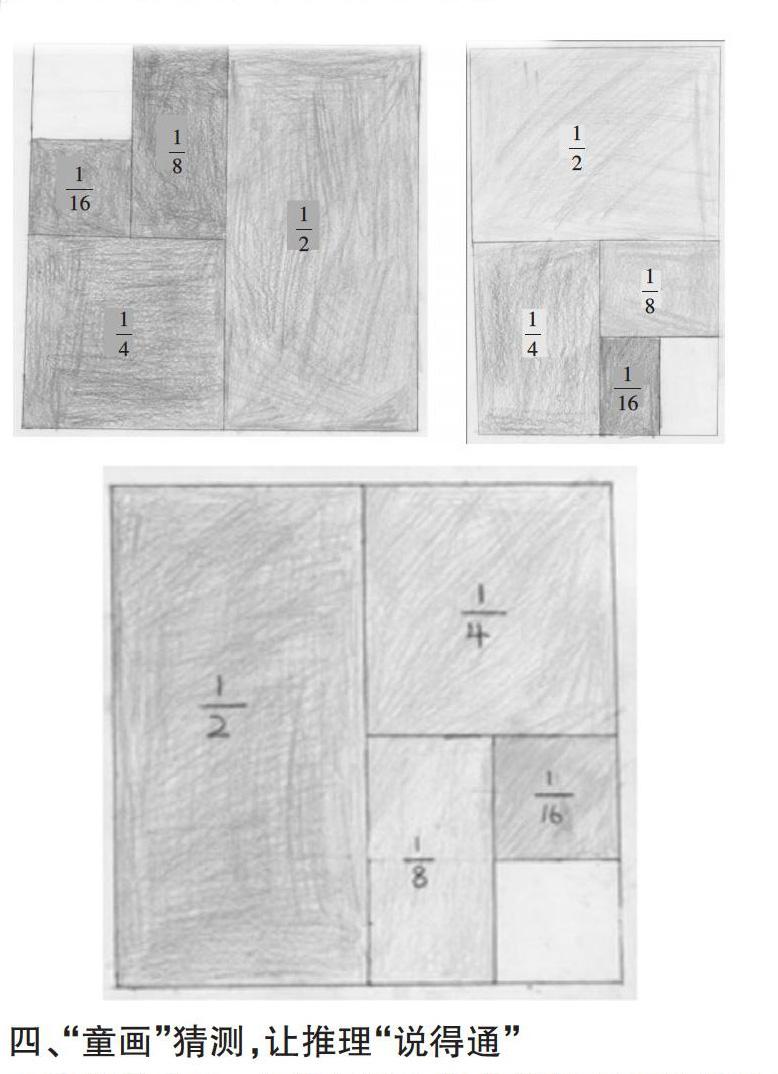
例如，在教學(xué)蘇教版教材五年級(jí)下冊(cè)“解決問(wèn)題的策略——轉(zhuǎn)化”第二課時(shí)時(shí)，我首先出示“[12+14+18+116+…+1256]”，然后提問(wèn)：“你準(zhǔn)備怎樣解決這個(gè)問(wèn)題？”多數(shù)學(xué)生都在沉思，沒(méi)有一個(gè)學(xué)生說(shuō)先通分再計(jì)算，說(shuō)明他們意識(shí)到這種類(lèi)型的題目不是用常規(guī)的方法就能解決的。于是我提示：“我們解決復(fù)雜問(wèn)題時(shí)要從簡(jiǎn)單的問(wèn)題著手，若要求[12+14+18+116]的值是多少該怎么做？現(xiàn)在請(qǐng)?jiān)谝粋€(gè)圖形上表示出每個(gè)加數(shù)，從圖上你會(huì)有什么發(fā)現(xiàn)呢？”學(xué)生動(dòng)手繪圖（如下圖），并根據(jù)圖示發(fā)現(xiàn)：[12+14+18+116]的和是從單位“1”去掉[116]的部分，就是[1516]。 這時(shí)我引導(dǎo)學(xué)生觀察這個(gè)加法算式中的加數(shù) ，思考它們有什么特征，從而總結(jié)概括出解決這類(lèi)問(wèn)題的方法，即轉(zhuǎn)化策略。這一過(guò)程是學(xué)生自主動(dòng)手探索的過(guò)程，也是體會(huì)轉(zhuǎn)化策略價(jià)值的過(guò)程。學(xué)生借助“童畫(huà)”，把思考過(guò)程說(shuō)得有條有理，很容易就能找到用轉(zhuǎn)化策略解決實(shí)際問(wèn)題的路徑及價(jià)值所在，達(dá)到用數(shù)學(xué)“童畫(huà)”表示，讓思路“看得見(jiàn)”的效果。

四、“童畫(huà)”猜測(cè)，讓推理“說(shuō)得通”

在數(shù)學(xué)教學(xué)中，應(yīng)培養(yǎng)學(xué)生的合情推理和演繹推理能力，鼓勵(lì)學(xué)生大膽猜測(cè)，并根據(jù)猜測(cè)進(jìn)行推理和驗(yàn)證，激發(fā)學(xué)生參與探索知識(shí)的興趣，鼓勵(lì)學(xué)生再造數(shù)學(xué)知識(shí)生成的過(guò)程，從而讓學(xué)生能有條理且清晰地表達(dá)自己的想法和看法。

例如，教學(xué)蘇教版教材五年級(jí)下冊(cè)“圓的面積公式”時(shí)，我設(shè)計(jì)了以下幾個(gè)教學(xué)環(huán)節(jié)：

（1）猜測(cè)。你認(rèn)為圓的面積與什么有關(guān)？圓的面積單位是平方厘米、平方分米、平方米，你認(rèn)為圓的面積與什么有直接的關(guān)系？學(xué)生都認(rèn)為圓的面積與半徑有關(guān)，而根據(jù)圓的面積單位，部分學(xué)生推測(cè)出圓的面積與半徑的平方有直接的關(guān)系。我接著追問(wèn)：“圓的面積會(huì)與圓的半徑的平方有什么樣的關(guān)系呢？你能在圓上畫(huà)一畫(huà)、找一找嗎？”

（2）嘗試。學(xué)生在自己所畫(huà)的圓上找它的面積與半徑的平方的關(guān)系。有的學(xué)生在半圓上畫(huà)出一個(gè)最大的三角形，三角形的底是圓的直徑，高是圓的半徑，于是得出三角形的面積是半徑的平方，半圓的面積小于這樣的三角形的2倍，大于一個(gè)三角形面積，從而推導(dǎo)出圓的面積是半徑的平方的3倍多一些。還有的學(xué)生在圓心角90[°]的扇形上畫(huà)一個(gè)邊長(zhǎng)和半徑長(zhǎng)度一樣的正方形，則半徑的平方表示一個(gè)邊長(zhǎng)和半徑長(zhǎng)度一樣的正方形的面積，正方形的面積大于扇形的面積，從而推導(dǎo)出圓的面積比半徑的平方的4倍要小一些。

（3）驗(yàn)證。“剛才僅僅是我們的猜測(cè)，還需進(jìn)行驗(yàn)證，能不能把圓轉(zhuǎn)化成我們學(xué)過(guò)的圖形呢？”學(xué)生首先想到把圓轉(zhuǎn)化成長(zhǎng)方形，于是他們根據(jù)書(shū)上的提示動(dòng)手畫(huà)一畫(huà)，小組內(nèi)合作完成。在大家的共同努力下，學(xué)生用“童畫(huà)”表示出從圓轉(zhuǎn)化成長(zhǎng)方形的過(guò)程。

（4）找聯(lián)系。“我們把圓轉(zhuǎn)化成長(zhǎng)方形，在這過(guò)程中什么沒(méi)變，什么變了？圓和長(zhǎng)方形有什么內(nèi)在聯(lián)系？”學(xué)生對(duì)照?qǐng)D示，在小組內(nèi)合作完成，找出它們之間內(nèi)在的聯(lián)系。不難發(fā)現(xiàn)，在轉(zhuǎn)化的過(guò)程中，面積沒(méi)變，長(zhǎng)方形的長(zhǎng)是圓周長(zhǎng)的一半，長(zhǎng)方形的寬是圓的半徑，從而推導(dǎo)出圓的面積是它半徑的平方的π 倍，從而驗(yàn)證剛才的猜測(cè)是正確的。

（5）總結(jié)概括。讓學(xué)生再一次對(duì)照?qǐng)D示回顧剛才推測(cè)、驗(yàn)證的過(guò)程，在回顧的過(guò)程中，學(xué)生再一次體會(huì)把圓轉(zhuǎn)化成長(zhǎng)方形，面積沒(méi)變，周長(zhǎng)變，長(zhǎng)方形的面積等于長(zhǎng)×寬，長(zhǎng)是πr，寬是r，從而得出圓的面積公式是S=πr2。

在上述教學(xué)中，教師引導(dǎo)學(xué)生直觀畫(huà)圖，獨(dú)立思考，并要求學(xué)生把自己的新想法和新體會(huì)在組內(nèi)進(jìn)行討論交流，逐步構(gòu)建起知識(shí)結(jié)構(gòu)，形成知識(shí)模型，在積累數(shù)學(xué)活動(dòng)經(jīng)驗(yàn)的過(guò)程中領(lǐng)悟數(shù)學(xué)思想，從而達(dá)到“童畫(huà)”猜測(cè)，讓推理“說(shuō)得通”的效果。

五、“童畫(huà)”表達(dá)，讓特征“說(shuō)得準(zhǔn)”

數(shù)學(xué)學(xué)習(xí)不光要讓學(xué)生知道是什么，還要讓學(xué)生經(jīng)歷探索認(rèn)知的過(guò)程，并且用自己喜歡的方式表達(dá)獲得知識(shí)的過(guò)程。學(xué)會(huì)用數(shù)學(xué)的方式去探索和思考是學(xué)習(xí)數(shù)學(xué)的關(guān)鍵，而將抽象的知識(shí)進(jìn)行可視化的表達(dá)，可以降低學(xué)生學(xué)習(xí)的難度。數(shù)學(xué)“童畫(huà)”能將抽象的知識(shí)用可視化的形式表達(dá)出來(lái)，具有直觀性和生動(dòng)性，非常有利于學(xué)生的思考和表達(dá)。因此，為學(xué)生營(yíng)造一定的探索氛圍和提供一定的現(xiàn)實(shí)背景是十分重要的。

例如，在教學(xué)蘇教版教材五年級(jí)下冊(cè)“3的倍數(shù)特征”時(shí)，我只讓學(xué)生猜測(cè)3的倍數(shù)特征，多數(shù)學(xué)生都說(shuō)個(gè)位上的數(shù)是3的倍數(shù)，那么這個(gè)數(shù)就是3的倍數(shù);接著我讓學(xué)生畫(huà)圖驗(yàn)證自己的猜測(cè)，學(xué)生畫(huà)計(jì)數(shù)器表示數(shù)，很多學(xué)生列舉了個(gè)位是3、6、9的數(shù)來(lái)驗(yàn)證自己的猜測(cè)，他們先舉了13、16、19這三個(gè)數(shù)，很顯然這三個(gè)數(shù)都不是3的倍數(shù)，然后他們?cè)谟?jì)數(shù)器上畫(huà)出了是3的倍數(shù)的數(shù)字。從中可以發(fā)現(xiàn)，3的倍數(shù)特征與這個(gè)數(shù)的個(gè)位數(shù)字沒(méi)有關(guān)系，而與這個(gè)數(shù)各個(gè)數(shù)位上數(shù)的和有關(guān);各個(gè)數(shù)位上數(shù)字的和是3的倍數(shù)，那么這個(gè)數(shù)就是3的倍數(shù)。學(xué)生借助“童畫(huà)”，很順利地發(fā)現(xiàn)了3的倍數(shù)特征，并用自己的語(yǔ)言準(zhǔn)確地總結(jié)概括出來(lái)。

總之，數(shù)學(xué)“童畫(huà)”體現(xiàn)“以生為本”的理念，用兒童的表達(dá)方式構(gòu)建和整合知識(shí)結(jié)構(gòu)，促進(jìn)新知從感性到理性的有效轉(zhuǎn)化，讓兒童的思維軌跡更清晰。

【本文系徐州市教育科學(xué)“十三五”規(guī)劃課題“數(shù)學(xué)‘童畫(huà)，讓兒童的思維過(guò)程看得見(jiàn)”的實(shí)踐研究（立項(xiàng)號(hào)：GH-13-18-L227）階段性成果。】

（責(zé)編 黃春香）