基于等壓差充電時間的鋰離子電池壽命預測

劉 健， 陳自強， 黃德揚， 鄭昌文， 周詩堯， 姜 余

(上海交通大學 海洋工程國家重點實驗室， 上海 200240)

近年來，鋰離子電池在電子產品、電動車、工業儲能等領域的應用越來越普及，鋰離子電池剩余壽命(Remaining Useful Life, RUL)預測有著重要的研究意義和實用價值.在充放電使用過程中，鋰離子電池會產生容量減少與內阻增大的現象，導致其性能不斷衰退，直至壽命截止.采用一定方法預測鋰離子電池的未來狀態與參數變化趨勢，可實現鋰離子電池壽命預測[1].

預測鋰離子電池壽命的方法主要有基于模型和基于數據兩類[1-4].為降低模型復雜度，基于模型方法也可通過經驗模型擬合電池容量退化曲線，并利用卡爾曼濾波、粒子濾波等進行模型外推實現RUL預測[5-6].基于數據方法如自適應滑動平均、支持向量機以及神經網絡等直接從數據中挖掘隱含的電池健康狀態信息及演變規律[7].但是，以上方法只能給出電池壽命預測的估計結果，不具備不確定性表達能力.

在線測量電池容量或阻抗等較為困難，若利用容量或阻抗數據進行電池壽命直接預測，往往因歷史數據有限而導致所建模型的精確性大大降低.針對直接預測電池壽命不易實現的問題，基于可監測的電流、電壓以及溫度等參數預測電池壽命的間接預測方法逐漸被采用.有研究者從放電過程入手構建了等時間放電壓差[8]、平均放電壓降[9]、放電電壓取樣熵[10]等健康因子.還有研究者采用混合動力脈沖測試的電壓取樣熵作為健康因子來估計電池容量變化以實現RUL預測[11].然而，基于放電過程的方法均基于恒流放電方式進行研究，而在實際應用中因工況變化和外界環境影響，大多數情況下電池無法滿足恒流放電的要求，因此該方法的實際應用受到限制.

針對上述問題，本文在恒流充電過程中提取等壓差充電時間序列，基于最小二乘法與容量建立廣義回歸線性模型；采用線性均值函數、平方指數協方差與周期協方差函數作為組合核函數建立高斯過程回歸模型；利用粒子群優化算法全局搜索最優超參數以優化模型；將等壓差充電時間作為健康因子，通過預測等壓差充電時間進行鋰離子電池壽命預測.

1 改進高斯過程回歸模型

1.1 高斯過程回歸模型

高斯過程回歸(Gaussian Process Regression, GPR)模型[12]是一種非參數模型，可通過先驗知識實現貝葉斯框架下的狀態預測，輸出預測均值、方差和置信區間，預測結果具備不確定性表達能力.GPR模型已廣泛用于股票預測、油井液面預測[13]以及時序分析預測[14]等領域.

考慮如下回歸問題

(1)

由式(1)得到y的先驗分布為

(2)

式中：Y為觀測值的集合，Y={y1,y2, …,yn}；X為訓練點集合，X={x1,x2, …,xn}；K(X,X)=[Kij]為n×n階對稱正定協方差矩陣，矩陣元素Kij=k(xi,xj)用來描述xi和xj之間的相關性，i=1,2,…,n，j=1,2,…,n；I為n階單位矩陣.

y和預測值的聯合先驗分布為

其中：f*為預測值的集合，f*={f(x*1),f(x*2), …,f(x*n)}；X*為測試輸入數據.

f*的后驗分布為

即預測值的集合f*的高斯過程回歸模型.其均值矩陣和協方差矩陣分別為

(3)

cov(f*)=K(X*,X)-K(X*,X)

(4)

模型預測輸出的95%置信區間為

確定均值矩陣和協方差矩陣后，通過訓練過程對超參數進行優化可得到GPR模型.GPR模型一般默認為零均值函數，常采用協方差函數作為平方指數函數：

(5)

超參數優化一般通過最大似然法和共軛梯度法實現，具體為：先求得訓練數據在條件概率下的負對數似然函數，再對超參數求偏導，最后采用共軛梯度法優化使偏導數取最小值得到超參數最優解，即可求解高斯過程模型.

1.2 組合核函數

在鋰離子電池的使用過程中，隨著電極和電解液中副反應的進行，鋰離子被不斷消耗，因此電池容量呈現退化趨勢.然而，在電池充、放電的間隙，副反應產品有可能消散.和前一個充放電循環相比，下一個循環周期的電池性能可能更好，電池容量有可能增加，此現象稱為容量再生[15].該現象造成鋰離子電池容量總體呈衰減趨勢，同時伴隨著局部動態波動變化.本文涉及容量為電池充滿電后在一定放電條件下完全放電所放出的最大可用電量.

為進行電池壽命的精確預測，需考慮鋰離子電池兩種不同的容量變化行為.因此，對于高斯過程回歸模型，僅單一形式的協方差函數不能滿足預測需求，需將多種協方差函數進行組合.在滿足非負定性的要求下，協方差函數相加或相乘，以構造組合協方差函數描述復雜問題[15].本文將容量再生現象近似看為正常容量退化趨勢上的周期性變化，故可選用周期協方差核函數:

其中：l2為方差尺寸；p為周期性參數.

在此基礎上選用平方指數協方差函數來描述局部性變化，將周期協方差函數和平方指數協方差函數的和作為組合協方差函數，使計算函數同時具備泛化能力和局部學習能力.均值函數選擇線性函數:

m(x)=ax+b

其中：a和b為任意常數.

1.3 粒子群算法

針對共軛梯度法對初始值依賴性強且易陷入局部最優等問題，選用粒子群優化(Particle Swarm Optimization，PSO)算法自動搜索最優超參數，以優化GPR模型.PSO算法初始化為一群隨機粒子，通過迭代尋找最優解，因此具備處理方便和全局優化等特點[14].

初始化粒子群后，更新粒子的速度和位置：

其中：zh、vh分別為第h個粒子當前位置和速度；m為當前迭代次數，最大迭代步數為100；w為慣性權重；c1為個體學習因子，c2為群體學習因子，c1和c2均為非負常數；r1和r2為分布在[0，1]間的隨機數.本文取粒子群規模為24，wmin=0.4，wmax=0.9，c1=2，c2=2.

將GPR模型訓練過程中的訓練值與實際值之間的均方誤差作為每個粒子的適應度值，以均方誤差最小為優化目標.在每一次迭代過程中，粒子通過跟蹤粒子本身最優解(P)和群最優解(G)更新個體位置.粒子每更新一次位置，通過比較新粒子和P、G的適應度值來更新P和G位置，直至達到目標閾值或最大迭代步數：

2 健康因子構建

2.1 實驗數據集

本文所用鋰離子電池的循環壽命實驗數據來自美國國家航空航天局 (National Aeronautics and Space Administration, NASA)卓越預測中心和馬里蘭大學的公開數據集[6].NASA卓越預測中心采用額定容量為2 A·h的18650型鋰離子電池在室溫下進行充電、放電和阻抗測試循環壽命實驗.具體過程為：先以 1.5 A的電流進行恒流充電，當電池電壓達到 4.2 V后轉為恒壓充電(截止電流為20 mA).然后，以2 A電流進行恒流放電，直至放電截止電壓，以電流倍率(C)表示電池充放電電流大小與電池額定容量的比率關系.在充電和放電過程中利用電化學阻抗譜測量電池的阻抗.本文選用其中B5和B6號電池，其放電截止電壓分別為 2.7，2.5 V，容量閾值均為 1.4 A·h.馬里蘭大學采用額定容量為 1.35 A·h的鈷酸鋰電池，其循環壽命實驗流程與NASA卓越預測中心的實驗方法相似，具體參數如下：恒流充電倍率為 0.5C，恒壓充電電壓為 4.2 V(截止電流50 mA)，恒流放電倍率為1C，放電截止電壓 2.7 V.本文選用其中的CX2-36、CX2-37號電池，容量閾值均為 1.08 A·h.

2.2 等壓差充電時間提取

在實際應用中，基于安時積分法測量鋰離子電池容量時存在累計誤差的問題.此外，大多數工況無法滿足電池恒流放電的要求，因此限制了基于恒流放電方式的間接預測方法的應用.而鋰離子電池充電過程不會受工況變化的影響，且多為恒流-恒壓充電方式，充電過程相對穩定,便于分析，因此本文從鋰離子電池充電過程中提取與壽命預測相關的健康因子.

從鋰離子電池循環壽命實驗數據中選取恒流充電過程進行分析，得到不同循環周期的恒流充電電壓與電流變化的關系，如圖1所示.圖中：I為電流；Ub為電池電壓；N為充放電循環周期.隨著電池充放電循環的不斷進行，電解液不斷消耗，極片活性不斷降低，電池阻抗增大、容量降低，充電時也較快達到截止電壓，恒流充電時間不斷減少.因此，采用鋰離子電池的電子產品在使用時間較長后，會出現充電迅速的現象.

圖1 B5電池充電電壓與電流變化曲線

將鋰離子電池每個恒流充電周期中電壓從低電壓升至高電壓的時間間隔稱為等壓差充電時間.在實際應用中，鋰離子電池滿充滿放情況較少，故本文選取恒流充電電壓從 3.9 V上升至 4.2 V的時間間隔作為等壓差充電時間.

B5鋰離子電池容量(Q)和等壓差充電時間(Δt)隨充放電循環周期的變化曲線如圖2所示.隨著電池充放電過程的不斷進行，等壓差充電時間整體呈衰減趨勢，且存在局部波動變化，與容量變化趨勢相似，兩者存在一定相關性.

圖2 B5電池容量與等壓差充電時間隨充放電周期的變化曲線

為進一步分析，應用線性基底擴展建立電池容量與等壓差充電時間的廣義線性回歸模型，可通過添加平滑函數來描述兩個變量之間的線性或非線性關系[16]：

Qi=AΔti+Bln Δti+E+εi

(6)

式中：Qi為第i個充放電周期的電池容量；Δti為第i個充放電周期的等壓差充電時間；A和B為預測因子的系數；E為常數；εi為誤差項.線性項AΔti用于改進等壓差充電時間的衰減過程，使其衰減過程的斜率與電池容量的退化過程一致；Bln Δti描述了電池容量和等壓差充電時間之間的非線性關系.

用誤差平方和(ES)和確定系數(RS)表示廣義線性回歸模型的誤差大小與擬合程度：

(7)

(8)

圖3 B5電池廣義線性回歸模型擬合曲線

所選4個電池的模型擬合評價結果見表1.可以看出，4個電池的ES值較小；除CX2-36電池外，其余3組電池的RS值均接近于1.說明所選模型的擬合效果較好，誤差較小.基于上述結果可知，等壓差充電時間和電池容量之間的相關性很高， 因此可以將等壓差充電時間作為健康因子進行電池的RUL預測.

表1 廣義線性回歸模型評價結果

2.3 基于等壓差充電時間的預測方法

在實際應用中，可在線采集鋰離子電池前k個充放電周期恒流充電過程中的等壓差充電時間序列數據，以充放電循環周期為輸入，相應的等壓差充電時間為輸出，結合訓練所采集的數據建立高斯過程回歸模型.基于廣義線性回歸模型得到電池壽命預測結果.

模型建立后，每到下一充放電循環周期，將在線獲取的新數據和之前獲取的數據同時訓練，建立新的高斯過程回歸模型.由于鋰離子電池壽命預測對實時性要求不高，所以在每個充放電過程中進行一次壽命預測.

3 實驗結果與分析

3.1 核函數的影響

選取B5鋰離子電池，以第100個充放電周期為預測起始點，以零均值函數和平方指數協方差函數作為基本核函數與 1.2 節中的組合核函數進行比較，結果如圖4所示.由圖4可知，基于組合核函數的GPR模型的容量隨充放電周期的增加呈衰減趨勢并伴隨局部波動變化，該變化規律與電池容量真實退化曲線相似.而基于基本核函數的GPR模型的容量預測曲線僅隨充放電周期的增加呈現總體退化趨勢，并無局部波動變化，未呈現容量再生現象，說明其預測效果較差.

圖4 B5電池兩種核函數的預測結果

以平均絕對百分比誤差(MAPE)和方均根誤差(RMSE)作為模型的電池容量預測評價標準：

(9)

(10)

MAPE和RMSE越小，模型的預測精度越高.4個電池基于組合核函數以及基本核函數的MAPE和RMSE計算結果見表2.可以看出，4個電池基于組合核函數的GPR模型容量預測的MAPE值低于2%，RMSE值不超過 0.020 A·h，均小于基本核函數的GPR模型預測誤差值，表明基于組合核函數的GPR模型預測精度更高.由于組合核函數的GPR模型能很好地預測容量再生現象，所以具備良好的泛化能力和局部變化學習能力.

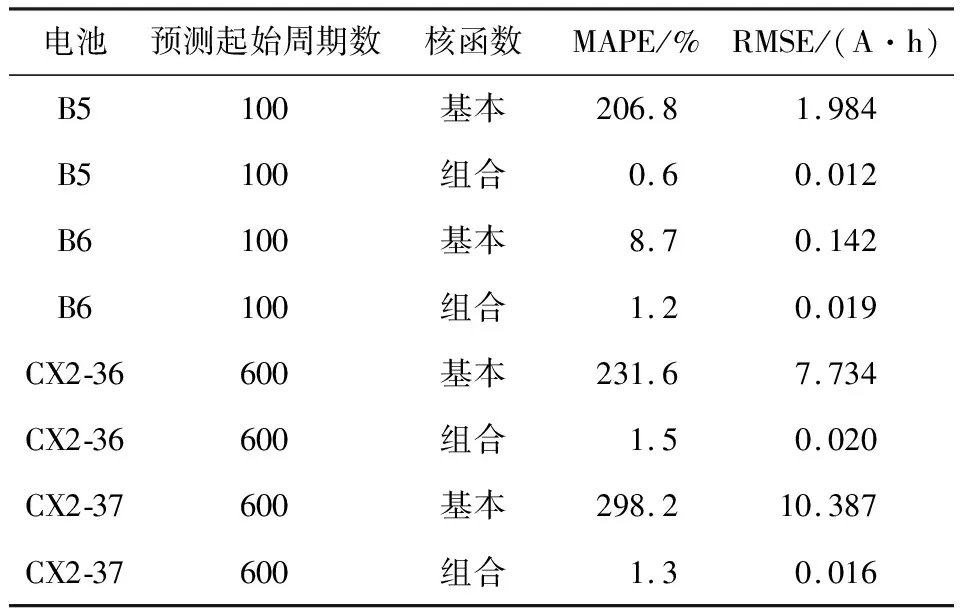
表2 兩種核函數的評價結果

3.2 基于等壓差充電時間的RUL預測

選取B5和B6鋰離子電池比較基于容量預測和基于等壓差充電時間預測的電池壽命，結果如圖5和6所示，其中基于Δt-Q預測為基于等壓差充電時間預測.基于容量(Q)預測是直接的預測方法，在離線狀態下利用充放電周期數和電池容量訓練GPR模型，將定充放電周期數作為輸入后直接輸出電池容量預測結果.B5、B6電池的等壓差充電時間預測曲線隨充放電周期增加呈衰減趨勢，伴隨著局部動態波動變化.基于容量直接預測的容量變化曲線和基于等壓差充電時間預測的容量變化曲線均呈現局部波動變化，但有時和容量真實變化趨勢相反，這是由于本文選擇的協方差函數是具有光滑和穩定性質所造成的.

圖5 電池等壓差充電時間預測結果

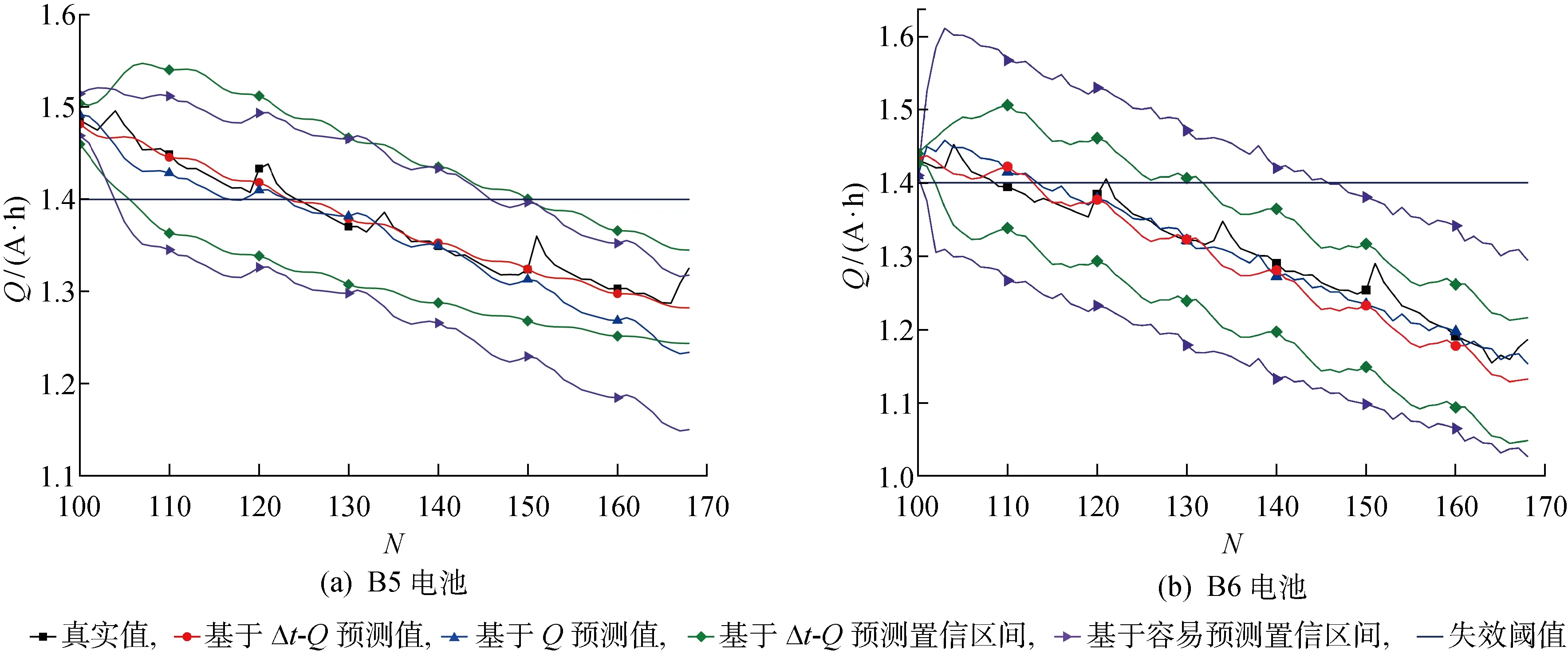
圖6 電池直接與間接RUL預測結果

4個電池在2個預測起始點基于上述兩種方法的壽命預測結果見表3.從表3中可以看到，對于B5和B6電池，2種方法的預測結果絕對誤差不超過5個周期；除B6在以第100 周期為起點的預測結果相對誤差較大外，其余預測誤差均在10%以內；CX2-36與CX2-37電池預測絕對誤差在20個周期以內.B6電池在以第100 周期為起點的預測結果相對誤差較大的主要原因是預測起始點離壽命截止點較近，容量真實曲線與預測曲線均波動變化，兩者存在一定偏離造成相對誤差偏大.GPR模型預測結果還會輸出置信區間.從表3可以看到，真實RUL值都在GPR模型預測的置信區間范圍內.對比分析發現，基于等壓差充電時間的壽命預測效果等同于基于容量的壽命預測，但基于等壓差充電時間測量的方法具有在線應用能力.

文獻[9]將電池恒流放電500～1 500 s之內的平均放電壓降作為健康因子，用二次函數 (Quadratic Function，QF) 擬合方法和基于快速邊緣似然最大化優化的相關向量機 (Optimized Relevance Vector Machine, ORVM)進行RUL預測，通過平均放電壓降閾值來判斷電池是否失效.選取B5鋰離子電池，將本文基于等壓差充電時間的GPR模型RUL預測結果與上述方法進行對比，結果見表4.通過對比可知，一方面，在兩個不同預測起始點，本文方法預測誤差分別為2個周期和1個周期，均小于優化相關向量機和二次函數擬合方法預測誤差；另一方面，從預測相對誤差來看，本文方法預測相對誤差在5%以內，優化相關向量機誤差在10%左右，二次函數擬合方法誤差在50%左右；最后，二次函數擬合方法預測結果不具備不確定性表達能力，而本文方法和優化相關向量機均可輸出置信區間，為預測結果提供更多參考信息.因此，本文基于等壓差充電時間測量的GPR模型RUL預測結果優于基于平均放電壓降的二次函數擬合方法和優化相關向量機方法.

通過分析不同種類電池的RUL預測結果、基于等壓差充電時間與基于容量的RUL預測結果以及基于等壓差充電時間與基于平均放電壓降的RUL預測結果，驗證了本文基于等壓差充電時間構建的鋰離子電池壽命預測方法的有效性、適應性及在線適用性.本文所提方法可用于實際應用中鋰離子電池壽命預測.

表3 4個電池的直接與間接RUL預測結果

表4 B5電池3種方法RUL預測結果

4 結語

本文針對鋰離子電池在線壽命預測及容量非線性退化問題，構建了基于等壓差充電時間的RUL預測方法.通過實驗證明本文所提方法可有效預測容量非線性退化軌跡，且具備良好的泛化能力和局部變化學習能力，容量預測的平均絕對百分比誤差值小于2%，方均根誤差值不超過0.020 A·h.具備在線應用能力的同時，具有較高的預測準確性及不確定性表達能力.預測效果等同于基于容量的直接預測，并且優于基于平均放電壓降的優化相關向量機方法.