高維最小二乘投影算法在NIR中的應用*
羅逸平,肖翠娥,傅建輝
高維最小二乘投影算法在NIR中的應用*
羅逸平,肖翠娥,傅建輝
(湖南城市學院 理學院,湖南 益陽 413000)
針對高維復雜的近紅外光譜(NIR)數據,提出了一種新的基于高維最小二乘投影的變量篩選方法(HOLPPLS)。首先計算高維最小二乘投影系數并對系數的絕對值進行排序,系數的絕對值越大,對應的變量就越重要;然后結合PLS進行變量篩選。HOLPPLS是結合了高維最小二乘投影和PLS的向前變量選擇算法。實際數據集的實驗分析表明,HOLPPLS能有效提高模型的預測性能。
高維最小二乘投影;偏最小二乘;NIR;變量選擇
針對復雜的近紅外光譜數據含有大量的冗余信息,同時具有很高的共線性[1],提出了一種新的基于高維最小二乘投影的偏最小二乘算法(HOLPPLS)。
高維最小二乘投影理論由WANG等2016年提出,他們指出在沒有強相關假設的條件下能夠給出可靠的變量選擇,計算復雜度較低[2]。
偏最小二乘(Partial Least Squares,PLS)算法由WOLD提出[3],已經成為近紅外光譜數據分析的最流行的方法之一。HOLPPLS算法結合了距離相關和PLS各自的優勢,實際的光譜數據集的實驗和分析表明,與常用的SRPLS算法比較,HOLPPLS方法的預測性能有明顯改進。
1 偏最小二乘回歸(PLSR)
PLSR是一種新型的多元統計數據分析方法,能夠有效地解決多維共線性問題,它已廣泛地應用在近紅外光譜(NIR)分析中。
設為和的線性組合,表示得分矩陣;為組合系數向量;為對最小二乘回歸系數向量。于是有下列公式:
=
=+=+=+(1)
式(1)中:為隨機誤差向量;==[1,2,…,p]t為維的系數向量。
2 高維最小二乘投影方法(High dimensional ordinary least squares projection,HOLP)
設光譜數據包個樣本,個變量,令={1,2,…,p},j=(1j,2j,…,nj)T(=1,2,…,)。是包含感興趣的屬性的維列向量。表示向量或矩陣的轉置。
在多元回歸分析中,經常考慮線性模型=+,=(1,2,…,p)T是回歸系數向量。高維最小二乘投影方法由XIANG等2016年提出,能夠有效地克服利用相關性大小來選擇變量的一些不足。高維最小二乘投影方法關系數計算公式為=T(T)-1。有關高維最小二乘投影方法的理論請參閱文獻[2]。值得注意的是,高維最小二乘投影篩選變量利用了中分量的大小排序,這一思想與使用同因變量的相關性大小來選擇變量是一致的。
3 高維最小二乘投影的偏最小二乘算法(HOLPPLS)
光譜數據往往包含噪聲、背景等無用信息。通常使用的PLS方法在建模時包含了所有的變量,這些可能會降低模型的預測精度。結合高維最小二乘投影和PLS的優點,提出了一種新變量選擇方法HOLPPLS。
HOLPPLS算法總結如下:①光譜數據矩陣和被標準化。令={1,2,…,p}表示整個的變量集。②計算高維最小二乘投影系數,依次挑選系數絕對值最大對應的一個變量,建立PLSR模型,然后記錄RMSE。這樣得到個PLSR模型和個RMSE。③選擇個RMSE值中最小的那個對應的變量集,然后在這個變量集上建立最后的PLS回歸模型。
4 數據與結果討論
選擇一個實際的近紅外光Gasoline數據集[4]來評估HOLPPLS算法的性能。作為參考標準,SRPLS(selectivity ratio pls)被用來作比較。
Gasoline數據是另一個近紅外光譜數據集,它包含60個樣本,近紅外譜根據漫反射度的函數log(1/R)從900 nm 到1 700 nm 中并以in 2 nm 為間隔測量出來的,于是一共有401個變量或波長(wavelengths)。60個樣本被隨機地分成訓練集(train set,35)、優化集(optimization set,15)和測試集(test set,15)。
數據集Gasoline的預測結果如表1所示。表1描述了Gasoline預測的結果。HOLPPLS方法比SRPLS獲得了更好的預測精度,選擇的變量數也更少。
表1 數據集Gasoline的預測結果
MethodsnLVnVarRMSE_OPTRMSEP_TESTThreshold SRPLS102610.1010.3430.012 HOLPPLS81080.0940.3190.036
HOLPPLS和SRPLS選擇的變量與波長區間如圖1所示。這些結果說明采用高維最小二乘投影系數篩選變量能夠改進PLS模型的預測性能。HOLPPLS算法是基于R語言(版本3.5.3)編寫的。
5 結論
利用近來提出的高維最小二乘投影方法,結合PLS的優點,提出了一種新的變量篩選方法HOLPPLS算法。
數據實驗表明HOLPPLS算法可以提高變量選擇和模型的預測性能。
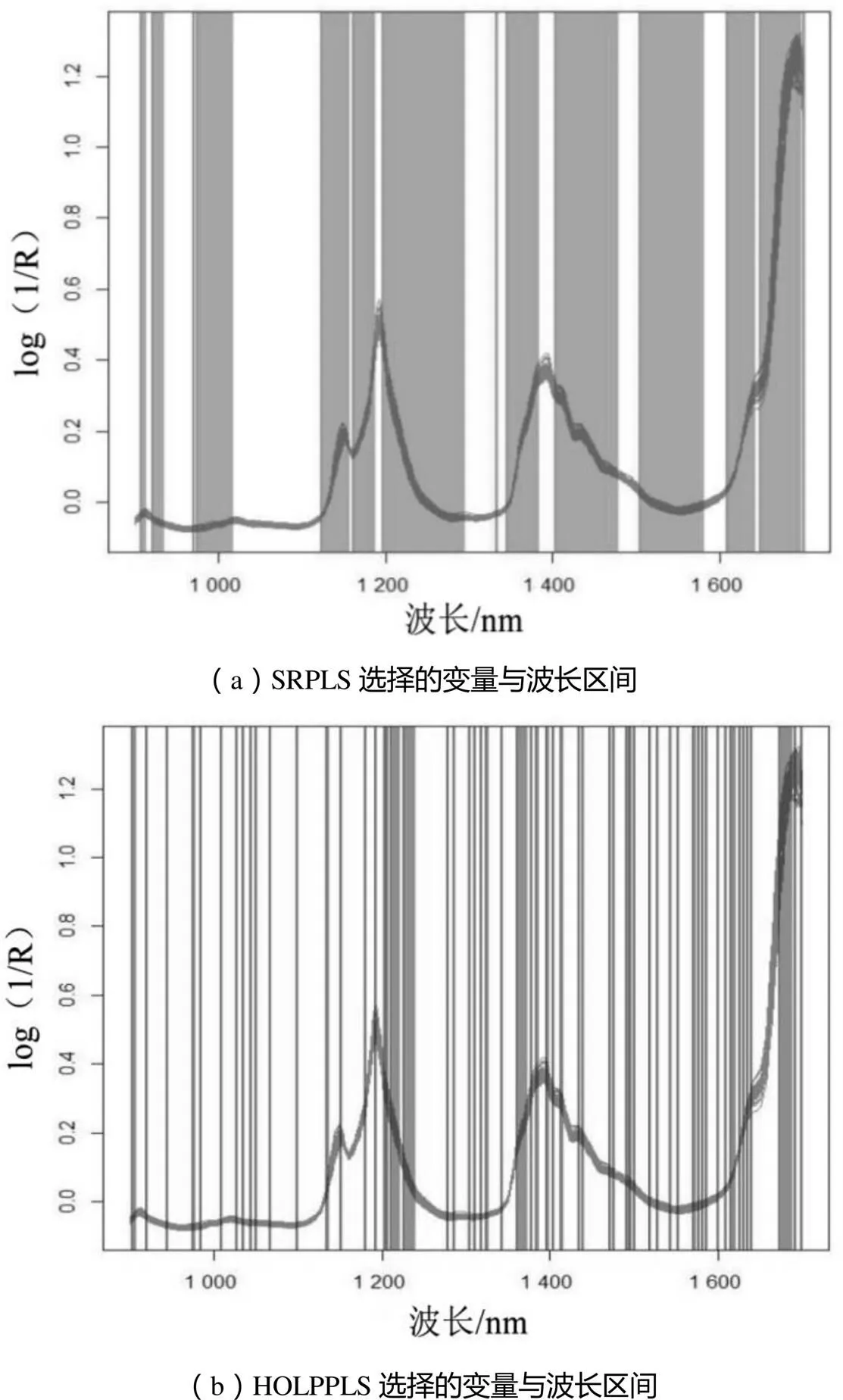
圖1 SRPLS和HOLPPLS選擇的波長變量
[1]LIANG Y Z,WU H L,YU R Q.Handbook of analytical chemistry 10 chemmometrics[M].3rd ed.Beijing:Chemical Industry Press,2016.
[2]XIANG Y W,CHEN L L.High-dimensional ordinary least-squares projection for screening variables[J].Journal of the Royal Statistical Society B,2016(78):589-611.
[3]WOLD S,ERIKSSON L.PLS-regression:a basic tool of chemometrics[J].Chemometrics and Intelligent Laboratory Systems,2001(58):109-130.
[4]ANDERSEN C M.Variable selection in regression-a tutorial[J].J Chemometr,2011(24):728-737.
O657.33
A
10.15913/j.cnki.kjycx.2019.18.037
2095-6835(2019)18-0092-02
湖南省教育廳項目“基于流形學習的統計建模方法在高維譜數據中的應用研究”(編號:16C0295)
羅逸平,男,湖南益陽人,碩士,講師,主要從事統計理論、數據分析等方面的工作。
〔編輯:嚴麗琴〕

